Extraction of the Extrinsic Base-Collector Capacitance
After calculating the values of pad capacitances, parasitic inductances and parasitic resistances, the small-signal model in the dashed box remains, whose Y-parameters (YEX) are determined by Equation (15). YINT are the Y-parameters of the intrinsic model.
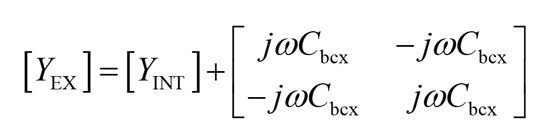
From Equation (15), the related expression of extrinsic base-collector capacitance is expressed in Equation (16).11
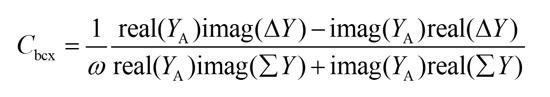
Where:


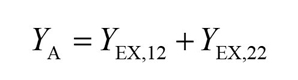
Extraction of Intrinsic Parameters
After peeling the extrinsic parameter Cbcx, the Z-parameters of the intrinsic model can be written as:
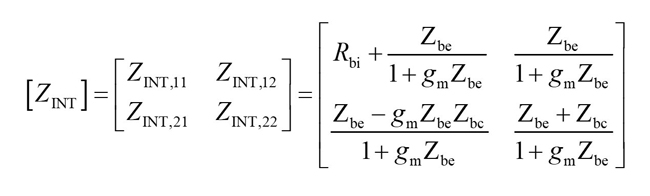
From Equation (20), the intrinsic base resistance Rbi can be determined.

After calculating the value of Rbi, it can be stripped from the intrinsic model. Then the resultant small-signal equivalent circuit, called IN, is shown in Figure 5. The Y-parameters of IN can be expressed as:

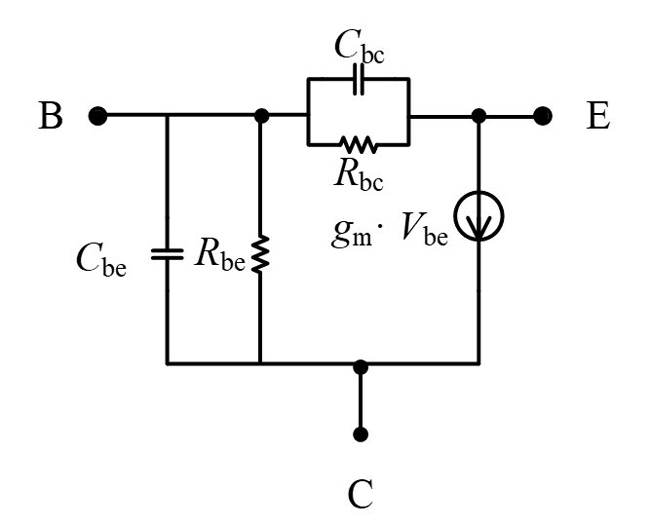
Figure 5 The equivalent circuit after peeling Rbi.
According to Equation (22), the other intrinsic parameters can be calculated with Equations (23) through (28).
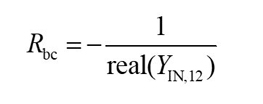
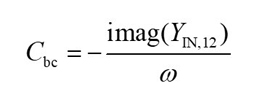

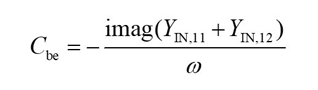
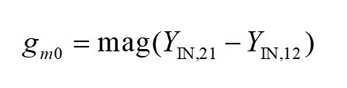
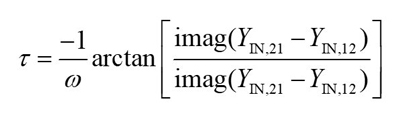
IGWO-BASED OPTIMIZATION TECHNIQUE
Overview of GWO
The grey wolf population can be divided into the leader wolf α, the deputy leader wolf β, the ordinary wolf δ and the bottom wolf ω according to the level mechanism from high to low. The lower the level, the greater the number of individuals. When wolves capture their prey, other individuals led by the leader wolf α systematically attack the prey, and then ω wolf follows the bits of α, β, δ wolves, updating its position step by step, which is the process of finding the optimal solution.
In GWO, the individual with the best fitness in the group is defined as α, the second-best individual is β, the third-best individual is δ, and the other individuals in the group are ω. The location of the prey is defined as the global optimal solution of the optimization problem.
Assuming that the size of the grey wolf population is N and the solution space is D dimensional, the update formulas of Xid(t+1) are described as follows:


Where Xp is the position vector of the prey, Xid(t) is the current position vector of the grey wolf, t is the current iteration, A is the convergence factor that controls the individual grey wolf to move toward or away from the current prey, B indicates the distance between a grey wolf and its prey and C represents the hindrance of nature that simulates the grey wolves in the process of rounding up their prey.
The formulas for A and C are:
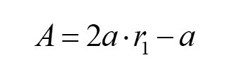
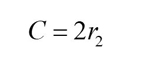

Where r1 and r2 are random numbers in the interval [0, 1] and a is the convergence factor, which decreases linearly from 2 to 0, and plays the vital role of adjusting the global search and local search of the algorithm.
The value of A is the value in the interval [−2a, 2a] and changes with a. Combining with Equation (19), the value of C is the random value in the interval [0, 2], which provides random weights for the position vectors of the three head wolves during the search process.
Thus, a certain random perturbation to the search process is formed and the algorithm can switch randomly between global search and local search. In addition, the value of C does not decrease with the iterative process, which is helpful to avoid falling into a local optimum. This is especially important in the late stage of the optimization process. Titeration is the maximum number of iterations.
The grey wolf population updates their respective positions Xα, Xβ, and Xδ according to α, β, and δ:
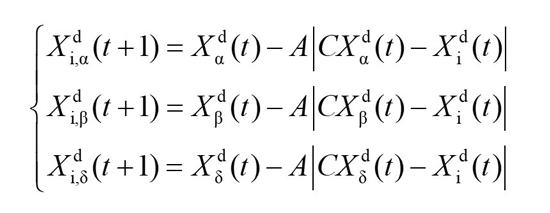

with
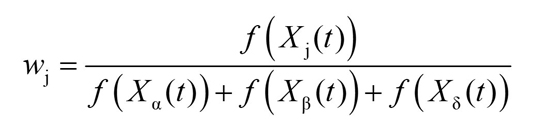
where d=1,2,3,…,D and f(Xj(t)) is the fitness of the grey wolf in the t generation.
Improved GWO
There are two random parameters, A and C, in the standard GWO algorithm, which play crucial roles in the study of the exploration ability and exploitation ability performance of the algorithm. It can be seen from Equation (31), that when |A| < 1, the grey wolf group narrows the encirclement and conducts a fine search in the local area, which corresponds to the local mining capability of the algorithm. Otherwise, when |A| > 1, the grey wolf group will expand the encirclement to explore better prey, which is the global exploration ability of the GWO algorithm.
Since the convergence factor a of the basic GWO algorithm is obtained by linear iteration, it cannot balance the global and local search ability. Chiu et al.29 proved that the linear convergence process is often not optimal for the update of important parameters. A depends heavily on the convergence factor a, which affects the exploration ability and exploitation ability of the algorithm. It can be seen from Equation (33) that a linearly decreases from 2 to 0 in the evolution process. However, the GWO algorithm needs nonlinear changes in the search process, and the linear decreasing strategy of the convergence factor a cannot realize the actual optimization search process.
Wen et al.30 and Nadimi-Shahraki et al.31 proposed that the convergence factor a changes nonlinearly with the number of evolution iterations, and the standard function test results show that the nonlinear change strategy achieves better optimization performance than the linear strategy.
Inspired by the inertia weight setting in the PSO algorithm, this work proposes a nonlinear convergence factor based on the tangent function shown in Equation (37)

Figure 6 shows that when the convergence factor a decreases linearly, the reduction rate remains unchanged during the iteration. The improved convergence factor a1 gradually decreases from slowly to quickly during the iteration. From the change of the slope of a1, it can be observed that the value of a1 remains at a high level and the declination speed is slow in the first half of the iteration, which is more conducive to a global search for the optimal solution. In the second half of the iteration, the value of a1 decreases faster, which finds the local optimum more accurately. Therefore, global and local searches achieve a more balanced condition.
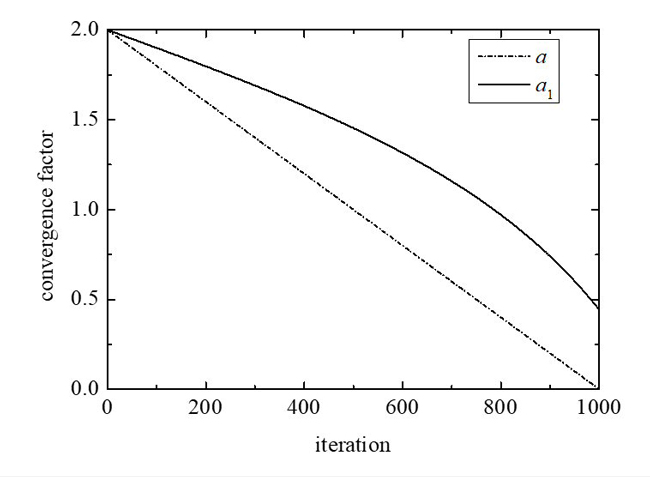
Figure 6 Variation curve of convergence factor.

