Small-Signal Model Parameter Optimization Process
Figure 7 summarizes the optimization flow of the IGWO algorithm for small-signal model parameters.
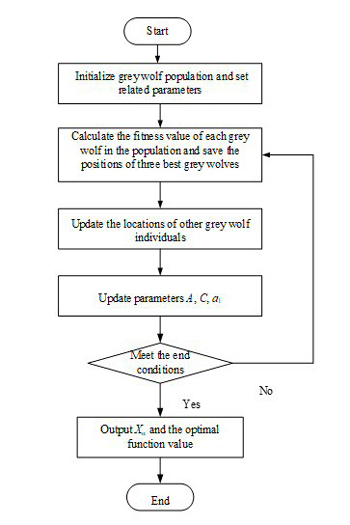
Figure 7 Flowchart of the IGWO small-signal model parameters optimization process.
Step 1. Initialization and setting related parameters.
The number of dependent-bias model parameters including intrinsic parameters and Cbcx constitute the solution space D of the IGWO algorithm. The location of the grey wolf population is initialized by Equation (38).
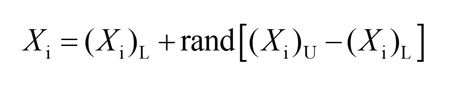
Where rand represents the random value in the interval [0,1]. (Xi)U and (Xi)L represent the lower bound (LB) and upper bound (UB) of dependent-bias model parameters. The total number of iterations Titeration and the population size N are set to constant values. The control parameters, such as A, C and a1, are randomly generated by the algorithm.
Step 2. Calculation of the fitness value of each grey wolf and saving the positions of the three best grey wolves.
The IGWO algorithm is based on the fitness value of individuals, so a reasonable fitness function can reflect the relative superiority and inferiority of each. The top three best grey wolves are selected according to the fitness value and their position vectors Xα, Xβ and Xδ are saved.
Step 3. Updating the positions of other individuals.
Equations (34) through (36) are used to update the positions of other individuals except the top three best grey wolves.
Step 4. Updating parameters.
Equations (31), (33) and (37) are used to update A, C and a1, respectively.
Step 5. Determination of termination conditions.
If the predetermined maximum number of iterations Titeration is reached, the calculation stops and the optimal position Xα and the optimal function value is output; otherwise, the executions of Steps 2 through 4 are repeated.
MODEL VALIDATION
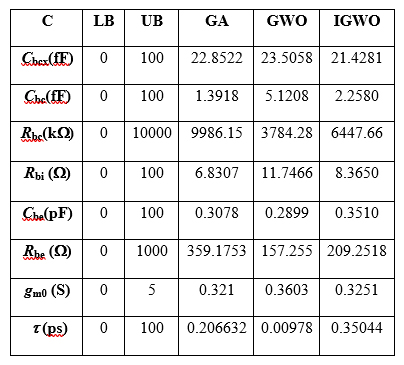
InP HBTs with emitter areas of 1×15 μm2 are used to verify the effectiveness of the proposed small-signal model. S-parameters are measured with an Agilent 8510C vector network analyzer and an Agilent B1500A semiconductor device analyzer provides DC bias for the device under test. The testing process is controlled by IC-CAP software. In this work, the dependent-bias model parameters of the InP HBT are optimized in the frequency range of 0.1 to 40 GHz using the GA, GWO and IGWO under two bias points (VCE = 0.7 V, IC = 4 mA and VCE = 2.0 V, IC = 7.5 mA). The used LB and UB with their optimized results are shown in Tables II and III.
TABLE II - OPTIMIZED PARAMETER VALUES FOR VCE=0.7 V, IC=4 mA
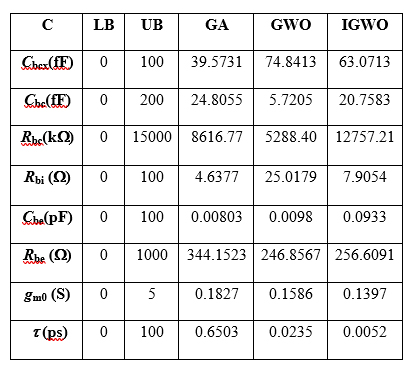
TABLE III - OPTIMIZED PARAMETER VALUES FOR VCE=2.0 V, IC=7.5 mA
The comparisons of measured S-parameters with simulated results adopting the GA, GWO and IGWO from 0.1 to 40 GHz are shown in Figures 8 and 9. It is apparent that IGWO-modeled S-parameters exhibit better agreement with measured results over the entire frequency range than GA and GWO-modeled S-parameters.
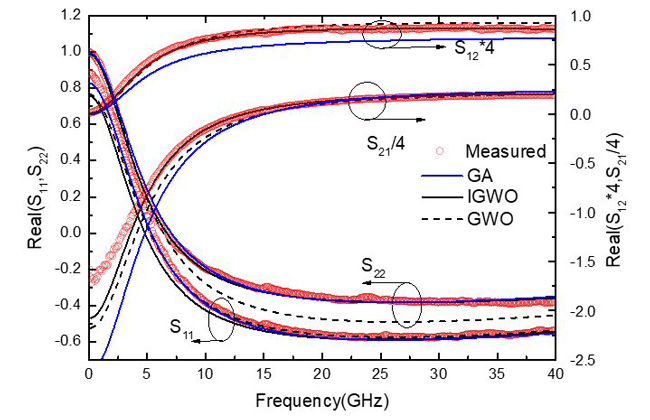
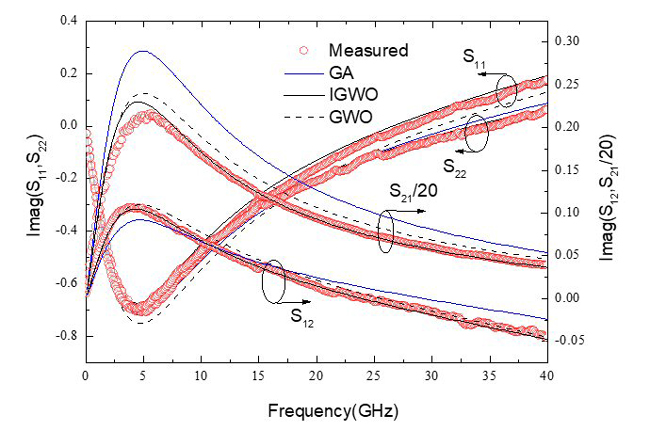
Figure 8 Comparison of measured and simulated S-parameters for VCE = 0.7 V, IC = 4 mA: real (a) and imaginary (b).
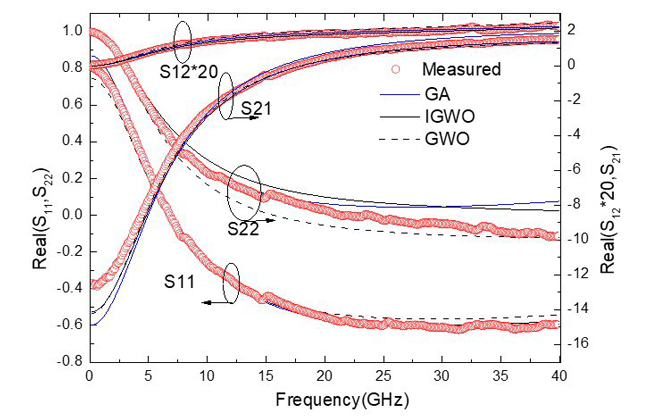
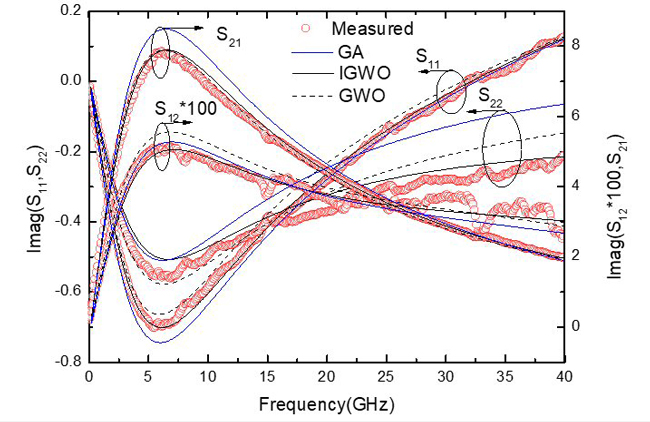
Figure 9 Comparison of measured and simulated S-parameters for VCE = 2.0 V, IC = 7.5 mA: real (a) and imaginary (b).
The accuracy of each method can be obtained more intuitively by calculating the S-parameter errors between the measured and the simulated values. The expression for the calculated error is given in Equation (39).
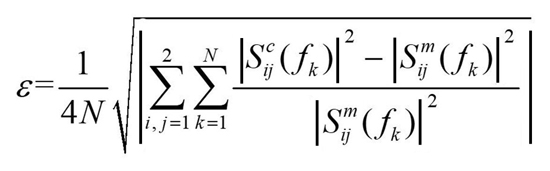
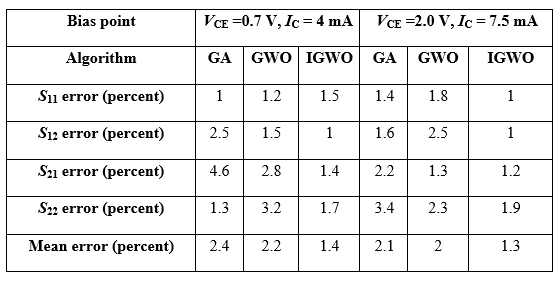
where Sm and Sc are the measured and simulated S-parameters, respectively. N is the total number of simulated points. The error results of different algorithms are shown in Table IV. The mean error obtained from IGWO is the smallest, verifying its superiority over the other approaches.
TABLE IV - ERROR RESULTS FOR DIFFERENT BIAS POINTS
CONCLUSION
The GWO algorithm is improved and successfully applied to optimize small-signal model parameters of HBT devices. The IGWO algorithm uses a nonlinear convergence factor based on the tangent function description instead of the linear decreasing convergence factor of the GWO algorithm. This effectively balances the global and local search ability.
The validity of the method is verified with an InP HBT in the frequency range of 0.1 to 40 GHz for two different bias conditions. It is proved that the IGWO-based optimization approach can yield more accurate small-signal model parameters than the GA and GWO algorithms. The algorithm is implemented in MATLAB and can be easily used to optimize small-signal model parameters of HEMT, SiC and MOSFET devices.
ACKNOWLEDGMENT
This work was supported by the Foundation of the Department of Science and Technology of Henan Province (Grant No. 222102210172, 212102210286).
References
- K. Song, J. Kim, H. Son, J. Yoo, M. Cho and J. -S. Rieh, “300-GHz InP HBT Quadrature VCO With Integrated Mixer,” IEEE Transactions on Terahertz Science and Technology, Vol. 10, No. 4, July 2020, pp. 419-422.
- Z. Griffith, M. Urteaga and P. Rowell, “A Compact 140-GHz, 150-mW High-Gain Power Amplifier MMIC in 250-nm InP HBT,” IEEE Microwave and Wireless Components Letters, Vol. 29, No. 4, April 2019, pp. 282-284.
- C. Yi, K. M. Lee, H. J. Kim and M. Kim, “WR-3.4 InP HBT Amplifier Module with Integrated Wideband Waveguide Transitions,” IEEE Microwave and Wireless Components Letters, Vol. 31, No. 12, December 2021, pp. 1315-1318.
- J. Zhang, B. Liu, M. Liu, L. Zhang and H. Jin, "A Watt-Level Broadband Power Amplifier in GaAs HBT Process,” Journal of Semiconductor Technology and Science, Vol. 19, No. 4, August 2019, pp. 357-363.
- L. Cheng, H. Lu, M. Xia, W. Cheng, Y. Zhang and Y. Zhang, “An Augmented Small-Signal Model of InP HBT with its Analytical-Based Parameter Extraction Technique,” Microelectronics Journal, Vol. 121, March 2022.
- A. Zhang and J. Gao, “An Approach to Determine Cutoff Frequency and Maximum Oscillation Frequency of Common Emitter Heterojunction Bipolar Transistor,” International Journal of Numerical Modelling, Vol. 33, No. 3, May/June 2020.
- Y. Zhang, Y. Chen, Y. Li, K. Qu and T. Ren, “Modeling Technology of InP Heterojunction Bipolar Transistor for THz Integrated Circuit: (Invited),” International Journal of Numerical Modelling, Vol. 33, No. 3, May/June 2020.
- A. Zhang and J. Gao, “A Direct Extraction Method to Determine the Extrinsic Resistances for an InP HBT Device Based on S-Parameter Measurement up to 110 GHz,” Semiconductor Science and Technology, Vol. 35, No. 7, June 2020.
- 9.A. Zhang and J. Gao, “An Improved Nonlinear Model for Millimeter-Wave InP HBT Including DC/AC Dispersion Effects,” IEEE Microwave and Wireless Components Letters, Vol. 31, No. 5, May 2021, pp. 465-468.
- S. Hu, K. Xu, S. Yu, Z. Wang, B. Zhou and Y. Guo, “Analysis of Nonlinear Large Signal Intrinsic Elements for InGaP/GaAs HBT Based on Gummel-Poon Model,” International Journal of Numerical Modelling, Vol. 33, No. 3, May 2020.
- J. -J. Qi, H. -L. Lyu, Y. Zhang, Y. -M. Zhang and J. -C. Zhang, “An Improved Direct Extraction Method for InP HBT Small-Signal Model,” Journal of Infrared and Millimeter Waves, Vol. 39, No. 3, June 2020, pp. 295-299.
- J. Zhang, M. Liu, J. Wang and K. Xu, “An Analytic Method for Parameter Extraction of InP HBTs Small-Signal Model,” Circuit World, Vol. 48, No. 4, November 2022.
- J. Zhang, L. Zhang, M. Liu and L. Zhang, “Systematic and Rigorous Extraction Procedure for InP HBT π-Type Small-signal Model Parameters,” Journal of Semiconductor Technology and Science, Vol. 20, No. 4, August 2020, pp. 372-380.
- H. Ghaddab, F. M. Ghannouchi, F. Choubani and A. Bouallegue, “Small-Signal Modeling of HBTs Using a Hybrid Optimization/Statistical Technique,” IEEE Transactions on Microwave Theory and Techniques, Vol. 46, No. 3, March 1998, pp. 292-298.
- Y. Li, Y. -Y. Cho, C. -S. Wang and K. -Y. Huang, “A Genetic Algorithm Approach to InGaP/GaAs HBT Parameter Extraction and RF Characterization,” Japanese Journal of Applied Physics, Vol. 42, No. 4B, April 2003, pp. 2371-2374.
- A. Jarndal, S. Husain and M. Hashmi, “Genetic Algorithm Initialized Artificial Neural Network Based Temperature Dependent Small-Signal Modeling Technique for GaN High Electron Mobility Transistors,” International Journal of RF and Microwave Computer-Aided Engineering, Vol. 31, No. 3, March 2021.
- S. Song, J. Ji, X. Chen, S. Gao, T. Zheng and T. Yuki, “Adoption of an improved PSO to Explore a Compound Multi-Objective Energy Function in Protein Structure Prediction,” Applied Soft Computing, Vol. 72, November 2018, pp. 539-551.
- S. Gao, K. Wang, S. Tao, T. Jin and J. Cheng, “A State-of-the-Art Differential Evolution Algorithm for Parameter Estimation of Solar Photovoltaic Models,” Energy Conversion and Management, Vol. 230, February 2021.
- M. Al Sabbagh, M. C. E. Yagoub and J. Park, “New Small-Signal Extraction Method Applied to GaN HEMTs on Different Substrates,” International Journal of RF and Microwave Computer-Aided Engineering, Vol. 30, No. 9, September 2020.
- A. Abushawish and A. Jarndal, “Hybrid Particle Swarm Optimization Grey Wolf Optimization Based Small Signal Modeling Applied to Devices,” International Journal of RF and Microwave Computer-Aided Engineering, Vol. 32, No. 5, May 2022.
- J. Jiang, T. Feng and C. Liu, “An Improved Nonlinear Grey Bernoulli Model Based on the Whale Optimization Algorithm and Its Application,” Mathematical Problems in Engineering, Vol. 2021, March 2021.
- B. Zolghadr-Asli, O. Bozorg-Haddad and X. Chu (2018). Dragonfly Algorithm (DA). In O. Bozorg-Haddad (Ed), Advanced Optimization by Nature-Inspired Algorithms. Studies in Computational Intelligence, Vol 720. Springer, Singapore.
- A. Jarndal, “On Modeling of Substrate Loading in GaN HEMT Using Grey Wolf Algorithm,” Journal of Computational Electronics, Vol. 19, No. 2, February 2020, pp 576-590.
- Z. Xu, H. Yang, J. Li, X. Zhang, B. Lu and S. Gao, “Comparative Study on Single and Multiple Chaotic Maps Incorporated Grey Wolf Optimization Algorithms,” IEEE Access, Vol. 9, May 2021, pp. 77416-77437.
- A. Seyyedabbasi and F. Kiani, “I-GWO and Ex-GWO: Improved Algorithms of the Grey Wolf Optimizer to Solve Global Optimization Problems,” Engineering with Computers, Vol. 37, No. 1, January 2021, pp. 509-532.
- M. A. Tawhid and A. M. Ibrahim, “A Hybridization of Grey Wolf Optimizer and Differential Evolution for Solving Nonlinear Systems,” Evolving Systems, Vol. 11, No. 1, March 2020, pp. 65-87.
- H. Y. Lu, W. Cheng, G. Chen, T. S. Chen and C. Chen, “Direct Extraction Method of InP HBT Small-Signal Model,” Applied Mechanics and Materials, Vol. 347-350, August 2013, pp. 1621-1624.
- Z. Jincan, L. Bo, Z. Leiming, S. Ligong, W. Jinchan and S. Lu, “A Rigorous Peeling Algorithm for Direct Parameter Extraction Procedure of HBT Small-Signal Equivalent Circuit,” Analog Integrated Circuits and Signal Processing, Vol. 85, No. 3, December 2015, pp. 405-411.
- C. Chui-Yu, S. Po-Chou and X. Li, “A Dynamic Adjusting Novel Global Harmony Search for Continuous Optimization Problems,” Symmetry, Vol. 10, No. 8, August 2018, p. 337.
- L. Wen, J. Jiao, X. Liang and M. Tang, “Inspired Grey Wolf Optimizer for Solving Large-Scale Function Optimization Problems,” Applied Mathematical Modelling, Vol. 60, No. 3, February 2018, pp. 112-126.
- M. H. Nadimi-Shahraki, S. Taghian and S. Mirjalili, “An Improved Grey Wolf Optimizer for Solving Engineering Problems,” Expert Systems with Applications, Vol. 166, March 2021.

