Recent developments have reinvigorated clinical investigations of hyperthermia (HT) as a viable adjuvant treatment in the fight against cancer. Researchers are placing a greater emphasis on multi-modal approaches that include mild temperatures (40° to 43°C) and standard therapies like radiation and chemotherapy, than on achieving higher temperature treatments (43° to 45°C), which were pursued in the past.
The emergence of robust computer simulation tools for accurate hyperthermia treatment planning has aided this resurgence by helping improve the quality of heating. This article outlines a recent collaborative study at Duke University to demonstrate the capabilities of a new suite of 3D electromagnetic and thermodynamic simulation tools for treatment planning of external hyperthermia treatments with a radio frequency (RF) phased-array heat applicator. Following a brief introduction to the rationale for moderate temperature hyperthermia and current methodology for heating tissue at depth in the body, the article will present a new approach for improved heating based on treatment planning with electromagnetic simulation software tools. Procedures, benefits and a comparison of simulated heating patterns with those measured in two clinical hyperthermia treatments of advanced fibrous histiocytoma (soft-tissue sarcoma) tumors will be presented.
Historical Background
Modern interest in hyperthermia began in the second half of the 19th century with a serendipitous clinical observation that some patients with externally visible tumors who experienced even moderate systemic temperature rise from a separate, severe illness experienced remissions of their tumors.1 Although intriguing, subsequent studies of fever induced therapy gave way around the turn of the century to a more intense interest in the oncological potential of the then newly discovered Roentgen Rays (X-rays). By the 1970s, frustrated with the limited success of radiation therapy for some resistant tumors, researchers returned to studies of the cell killing potential of heat as an adjuvant therapy to enhance the effects of radiation.2 By 1984, hyperthermia was an approved medical treatment for superficial tumors that could be heated with the equipment available at that time.
New Biological and Clinical Rationale
Bolstered by research in the 1980s emphasizing the cell killing potential of heat, researchers focused on high temperature hyperthermia (> 43°C) treatments intended to induce cell death. Unfortunately, this approach was limited by a number of biological, technological and commercial factors. As a result, interest in hyperthermia suffered a setback in the mid-1990s.3 Fears of thermotolerance, for example, limited the number of heat fractions to about two per week. Thermotolerance in surviving cells increases with temperature; however, its effect is now known to be limited in tissues treated with mild-temperature HT.
Heating tissue above 43°C also causes vascular damage, thereby inducing hypoxia, whereas the presence of oxygen is critical to the effectiveness of both radiation- and chemo-therapies. It is now understood that mild HT leads to increased blood perfusion and pO2 (reoxygenation) of fast-growing hypoxic tumors that have outgrown their local blood supply, thus enhancing radio- and chemo-sensitization. Furthermore, because of the threat of vascular damage and hypoxia, heat was often applied after radiation, which can reduce the effectiveness of the HT in terms of reoxygenation. Finally, studies have shown that mild HT results in the denaturation (unfolding) and eventual aggregation of nuclear proteins, processes that interfere with mitosis, DNA transcription and DNA repair.
A noted absence of detrimental clinical effects of thermotolerance and overwhelming evidence of positive effects from tissue reoxygenation and increased denaturation/aggregation potential are the key biological factors encouraging scientists to rethink adjuvant mild hyperthermia.
Accompanying Technological and Commercial Considerations
A typical course of clinical hyperthermia treatments consists of four to eight heating sessions, spread over a period of several weeks. The first hour of a two-hour session is used for patient preparation, such as placement of thermal monitoring probes in and around the tumor volume and the placement of the RF applicator around the tumor region. After the patient is prepared, power is supplied to the applicator’s antenna(s) and the tumor is heated by radiated electromagnetic energy.4
Though the principles of tumor heating are widely understood, the technology to focus heat into a desired tumor volume at depth in the body has lagged behind the theory, especially for deep-seated malignant tumors. For regional hyperthermia of deep-seated tumors, electromagnetic annular phased-array applicators (including smaller sized mini-annular phased-array (MAPA) applicators that fit around one extremity) have been developed for the frequency range of 75 to 150 MHz.5-7 To focus the heat into the tumor site, researchers have found that the driving phases and amplitudes of the MAPA must be carefully controlled.
Equipment considerations also damaged initial perceptions of hyperthermia and have significantly slowed acceptance of this clinical modality. Limited adjustability of applicator power deposition patterns led to poor control of heating, which has restricted the number of locations to which HT could be reliably applied. Even for multiple antenna arrays, inflexible and klunky controls made beam focusing and steering slow and imprecise. Delivering the required power to the target also presented a challenge. The absence of robust computer simulations often left clinicians to deal with superficial “hot spots”—in some cases leading to undesirable blisters or burns on the skin surface (air-dermis interface). The absence of noninvasive thermometry forced HT technicians to rely on a very limited number of implanted temperature probes. Insurance controlled cost codes and restrictive reimbursement rates have also played a role in encouraging OEMs to forego development plans. Happily, many of these technical challenges have been addressed in the last 10 years and promising solutions are emerging.
The Duke Study: Equipment, Methods and Results
Power Delivery System

Figure 1 Schematic of the power delivery system.
In Figure 1, a schematic overview of the RF power delivery system is presented. A Lucite cylinder with a single ring of eight dipole antennas connected in parallel pairs sits directly over a soft tissue sarcoma of the lower leg, as shown in Figure 2. During treatment of Cases I and II, the applicator was positioned below the patient’s knee. Filters and matching feed network were designed to deliver up to 50 W per dipole pair at a frequency of 140 MHz. Frequency selection is a trade-off between beam size and penetration depth. Higher frequencies have smaller beam widths and shorter penetration depths. A water bolus was used to reduce concomitant hot spots and to improve the radiation efficiency of the electrically short dipoles. Water is an ideal waveguide medium for two reasons. First, its electrical properties are closely matched to that of human dermis so the applied energy can be transmitted through to the tumor. Impedance mismatches and changes of wavelength at dielectric interfaces cause reflections and hot spots. Second, water has a high heat capacity and is therefore an excellent thermal coolant of the skin surface.

Figure 2 Applicator in situ.
Measuring Temperature to Confirm Simulation Results
Information about each structure and target volume of a patient can be obtained by utilizing computed tomography (CT) or other medical imaging modalities, as shown in Figure 3. The sarcoma tumor, located in the patient’s lower leg, is surrounded by a water bolus inside a 26 cm diameter, four-antenna phased-array applicator. The patient is supine. The tumor region is indicated by white arrows. In this study, two interstitial temperature probes were inserted into the tumor and surrounding healthy tissue. These local probes were used to confirm the simulation results.

Figure 3 Cross-sectional view of sarcoma tumor.
Simulation Methods and Procedures
Due to the recent advent of accurate 3D electromagnetic and thermal simulation software programs, pre-treatment planning of complex heterogeneous tissue regions is now possible. First, the antenna array and tissue properties are entered into the EM solver with appropriate geometry, and specific absorption rate (SAR) distributions are calculated. These SAR distributions can then be automatically fed into a bio-heat transfer equation-based thermal solver to produce expected 3D temperature distributions in the tissue.
The simulation strategy is:
Step 1: Use 3D FEM simulator (HFSS) to solve for EM fields in the volume of interest.
Step 2: Insert the EM field inputs from HFSS into the 3D FEM thermodynamic simulator (ePhysics) to produce temperature distribution from bio-heat transfer equation calculations in the volume of interest with assumed perfusion values that bracket the expected range in tumor and normal tissues.
Although exact temperature maps are not possible, due to uncertain tissue perfusion which varies spatially and temporally during treatment, these SAR and estimated temperature maps help clinicians pre-plan dosage and avoid patient hot-spots. They allow technicians to determine appropriate field amplitude and phasing, which are used to control beam steering. Simulations also help engineers test new applicator designs and provide educational training aids for pretreatment planning optimization of optional heating configurations and approaches.
In this study, an electromagnetic and thermodynamic co-simulation approach using accurate tissue properties and anatomy from a complete human body model was correlated against direct measurements. The effective energy exchange between the power delivery system and the tumor is determined in two steps. First, a 3D, finite element electromagnetic simulator is used to predict the electric field in the tissue region of interest (that is the leg). The solved electric field data are converted to SAR inputs according to the following equation:

where σ is the tissue electrical conductivity, ρ is the tissue density and E is the electric field. In the second step, the SAR data from the electromagnetic simulator is then “linked” to a thermodynamic simulator and the bio-heat transfer equation is solved for changes in temperature (ΔT):

where Τ is the temperature (°C), t is the time (s), r is the tissue density (kg/m3), Κ is the thermal conductivity (W/(m • K)), c is the tissue specific heat (J/(kg • K)), F is the blood flow rate or perfusion (m3/(kg • s)) and the subscript “b” refers to blood. This energy balance (Equation 2) relates the rise in temperature over time at a given region of interest to the heat inputs (power deposition or SAR) and heat losses from thermal conduction and convection (blood perfusion). As will be shown in the test case results below, the blood perfusion factor represents the greatest source of uncertainty. Several initial simulations were run to bracket the expected range of tumor perfusion. Figure 4 summarizes the overall simulation strategy.

Figure 4 Summary of simulation strategy.
Procedures
Step 1: Producing the EM Model and Simulation
The applicator with paired dipole antennas and tuning stub feed network was first drawn in a mechanical CAD program. The drawing file was translated and imported into the electromagnetic simulator. The amplitude and phase inputs to each dipole were adjusted for optimum tumor focus. Next, a recently released 300-component human body model was called by the EM simulator. To reduce simulation time, all non-essential distal body components such as head or arms were de-featured (turned off).
A model of the sarcoma bearing leg was created starting from a “generic patient” computed tomography (CT) database into which the tumor volume was inserted at the appropriate location. The electrical properties were entered for each component of the model and the EM simulation initiated. The FEM-based EM simulator first produces a tetrahedral mesh for each model component using an adaptive meshing algorithm. This algorithm automatically adds more tetrahedra to regions experiencing large changes in the electric and magnetic field quantities being solved. Once the mesh is complete, the field solver solves Maxwell’s equations for each tetrahedron.
The solved 3D EM field model is then linked (“data-linked”) to the 3D thermodynamic solver. Data linking allows changes in the EM model, for example amplitudes and phases fed to the dipole pairs, to be automatically updated in the 3D FEM thermodynamic model. The resulting field quantities are then used to produce the SAR inputs in the thermodynamic simulator.
Step 2: Simulation of the Thermodynamic Model
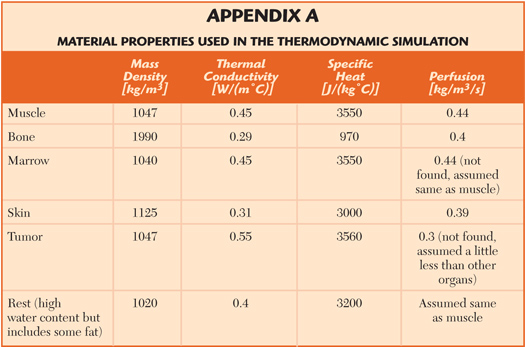
Appendix A Material Properties Used in the Thermodynamic Simulation
The thermodynamic simulator uses the same 3D applicator-body model as the EM simulator. A mesh is produced and the temperature changes within each tetrahedron are derived as a function of time. To complete the thermodynamic model, material properties, including mass density, thermal conductivity and specific heat, for each component were entered. These data were derived from a literature search and are summarized in Appendix A.8,9 When a range of values appeared in the literature, an average value derived from the range was used. In addition, the bolus was assumed to form a constant temperature thermal sink. Based on bolus dimensions and the volumetric flow rate of water within the bolus, an interface (forced convection boundary) temperature of 24°C was assumed.
Baseline blood perfusion values were derived from a literature search and are summarized in the table.10 To provide a more realistic model of variable tissue perfusion during heat treatments, a temperature dependent perfusion model was created. This model was based on perfusion data of a dog’s prostate taken from the CRC Handbook of Thermal Engineering. According to the model, the perfusion factor F, in Equation 2, was multiplied by a temperature dependent factor ranging from 1 to 1.52. This temperature dependent perfusion model was used to account for the clinical observation that perfusion increases in response to gentle heating. In addition, the perfusion value for the skin layer was assumed to increase by a factor of five when the skin is warmed. However, due to the overall mass of the skin, this additional perfusion had little effect on the simulation results.
Results
Case I
The first case was used as a baseline to determine the correlation between measurement and simulation. As shown previously, two in situ probes were used. The first was located centrally within the tumor and the second was placed in healthy tissue to the left of the tibia. During the first 18 minutes of treatment, the four dipole pairs were driven with equal amplitudes and phases at 140 MHz.
This phasing resulted in a beam that was focused centrally in the roughly cylindrical volume of interest and heated the surrounding tissue almost equally,5 except as modified by heterogeneous electrical and thermal tissue properties. Both the healthy tissue and malignant tissue were heated.
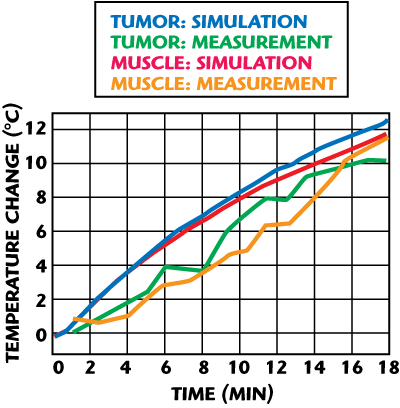
Figure 5 Case I: Temperature changes in tumor and muscle.
The temperature data for the in situ probes is compared to the simulation results in Figure 5. Here, the perfusion values shown in the table and the temperature dependent model were used in the simulation. A high correlation between simulation and measurement was found for both the tumor and the healthy tissue. These results were encouraging and the investigators were able to proceed to a subsequent, more complex clinical trial.
Case II
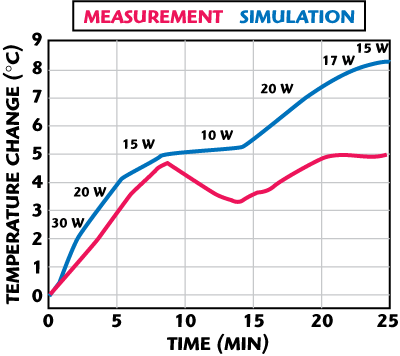
Figure 6 Case II: 25 minutes with variable power, equal phases.
In the second clinical study, an attempt was made to maintain a constant temperature rise in the tumor by adjusting the total input power to the dipole pairs during the treatment. As before, the four dipole pairs were driven with equal power and phase. For the first two minutes, 30 W were applied to each of the four dipole pairs. From minutes two to five, 20 W were applied, and so on as indicated in Figure 6. After the treatment, the applied power changes were simulated. As shown, there is fairly tight correlation between measurement and simulation for the first 10 minutes. Thereafter, for approximately five minutes, the curves begin to diverge. Eventually, at approximately 15 minutes, trends realign, but with a two degree separation.
After studying the data and their sensitivity to various parameters, it was postulated that the effect of perfusion was still being underestimated—even with the temperature dependent model. Subsequent simulation studies were performed to confirm this view.

Figure 7 The effect of perfusion.
Since the sensitivity study strongly hinted that the perfusion values were too low, and since there was not enough information to include detailed modeling of complex arteries and veins during this trial, an iterative series of simulations was conducted with increasing perfusion factors. A marked improvement in the correlation in Case II was observed using a perfusion value that was double the initial value. Both cases were re-simulated with the new perfusion factors and compared to the measured results. As shown in Figure 7, both cases demonstrated a marked improvement in the correlation of simulated and measured data.
Discussion
A number of investigative pathways are renewing interest in adjuvant mild hyperthermia in the fight against cancer. Critical among these is the development of simulation tools that allow clinicians the opportunity to optimize the heat dosage and prevent patient hot spots. Inspired by the goal that one day researchers will be able to accurately predict the temperature distribution before a clinical hyperthermia treatment for each patient, much effort has been done in the area of computer modeling and simulation.1 As argued in THE LANCET Oncology (August, 2002), “The potential to control power distributions in vivo has been significantly improved... by the development of planning systems and other modeling tools.” These simulation tools are also being used to design new applicators and train the next generation of medical researchers.
To achieve these goals, two steps are required. The first step is to determine the E-field distribution in heterogeneous tissue, which, when coupled with respective tissue properties, determines the power deposited per unit volume or mass (SAR). Secondly, using the knowledge of spatial and time dependent SAR distribution, coupled with the thermal properties, one can predict the transient and steady state temperature distributions. Ideally, one needs accurate patient specific anatomic and physiologic tissue models and complete understanding of the electrical and thermal properties of malignant and surrounding healthy tissue. Clearly, a very complex model is required. However, some of the critical information is not completely known, such as blood perfusion. Studies on blood perfusion in tumors show that the value varies significantly with tissue type, as well as temperature and other physiologic conditions.11 But no specific value for human tumor can be identified accurately in advance. Of all these factors, the effect of local tissue temperature on muscle perfusion is the easiest to study. Research in this area has been done by different groups. The information used herein for the temperature dependence of blood perfusion is from the CRC Handbook of Thermal Engineering. This reference provides a few perfusion multipliers for dogs’ prostate over a range of temperatures. In this study, the initial perfusion increased 17 percent when temperature exceeded 39.6°C and 52 percent when temperature reached 41.7°C.
Conclusion
In this study, a novel coupled electromagnetic and thermal simulation procedure is described that combines 3D FEM electromagnetic and thermodynamic simulators with an advanced human body model that incorporates accurate anatomic geometry and corresponding tissue properties. An assumption of temperature dependent blood perfusion has been investigated. Two clinical hyperthermia treatments of an advanced soft tissue sarcoma of the leg are simulated and results compared to simulations. The comparison of simulated and measured thermal data are shown to have a high degree of correlation if blood perfusion is considered, proving the importance of perfusion modeling for clinical applications.
Acknowledgments
This project was supported by NIH grant 5PO1-CA042745. The authors would like to express their appreciation to a large number of collaborators at Duke University Medical Center who participated in collaborative efforts that contributed to the investigation reported here. The first author also gratefully acknowledges the support and helpful discussions from the software development group at Ansoft Corp.
References
1. S.B. Field and J.W. Hand, An Introduction to the Practical Aspects of Clinical Hyperthermia, Bigger Books, 1990.
2. J. v.d. Zee, “Heating the Patient: A Promising Approach,” Annals of Oncology, Vol. 13, No. 8, August 2002, pp. 1173-1184.
3. M.W. Dewhirst, L. Prosnitz, D. Thrall, D. Prescott, S. Clegg, C. Charles, J. MacFall, G. Rosner, T. Samulski, E. Gilette and S. LaRue, “Hyperthermic Treatment of Malignant Diseases: Current Status and a View Toward the Future,” Seminars on Oncology, Vol. 24, 1997, pp. 616-625.
4. A.J. Fenn and G.A. King, “Adaptive Radiofrequency Hyperthermia Phased-array System for Improved Cancer Therapy: Phantom Target Measurements,” International Journal of Hyperthermia, Vol. 10, 1994, pp. 189-208.
5. Y. Zhang, W.T. Joines, R.L. Jirtle and T.V. Samulski, “Theoretical and Measured Electric Field Distributions Within an Annular Phased Array: Consideration of Source Antennas,” IEEE Transactions on Biomedical Engineering, Vol. 40, No. 8, August 1993, pp. 780-787.
6. P. Wust, R. Beck, J. Berger, H. Fähling, M. Seebass, W. Wlodarczyk, W. Hoffman and J. Nadobny, “Electric Field Distributions in a Phased-array Applicator with 12 Channels: Measurements and Numerical Simulations,” Medical Physics, Vol. 27, No. 11, November 2000, pp. 2565-2579.
7. L. Wu, R.J. McCough, O.A. Arabe and T.V. Samulski, “An RF Phased-array Applicator Designed for Hyperthermia Breast Cancer Treatments,” Physical Medical Biology, Vol. 51, No. 1, January 2006, pp. 1-20.
8. H.S. Hatfield and L.G.C. Pugh, “Thermal Conductivity of Human Fat and Muscle,” Nature, Vol. 168, No. 4282, November 24, 1981, pp. 918-919.
9. H.F. Bowman, “Heat Transfer and Thermal Dosimetry,” Journal of Microwave Power, Vol. 16, No. 2, 1981, pp. 121-133.
10. L. Shargel and A.B.C. Yu, Applied Biopharmaceutics and Pharmacokinetics, Fourth Edition, McGraw Hill/Appleton and Lange, 1999.
11. S. Fujita, M. Tamazawa and K. Kuroda, “Effects of Perfusion Rate on the Optimization of RF-Capacitive Hyperthermia,” IEEE Transactions on Biomedical Engineering, Vol. 45, No. 9, September 1998, pp. 1182-1186.
