Metamaterial-based Compact Multilayer Filter with Skew-symmetric Feeds

Microwave filters are an essential component in modern wireless communication systems. It is important to reduce their size and weight in order to integrate them with other components in a single chip system.¹ Using a multilayer filter is the main trend in filter design, since it shows a better performance than a planar version.²

At microwave frequencies, a negative permeability can be realized over a given frequency range in the magnetic resonance frequency of a periodic array of SRRs.³ In this article, a multilayer technology and an SRR structure are combined for the design of a novel multilayer filter.

Compared with the conventional microstrip filter, the proposed filter shows a significant size reduction and an improved selectivity. The measured results have a good agreement with the simulated results.

Theory

Figure 1 Schematic drawing the SRR.

The SRR, shown in Figure 1, is made of two concentric rings separated by a gap, both having splits at opposite sides. The geometrical parameters, such as the split gap width, gap distance, metal width and radius are respectively represented by d, t, w and r. The subscripts i and o denote the inner and outer rings. Besides the electric and magnetic coupling, the incident field also induces the magnetoelectric coupling. The SRR not only has an electric resonance, but also a magnetic resonance. Moreover, the magnetic resonance frequency is lower than the electric resonance frequency.⁴ Using the magnetic resonance of the SRR in the filter design, a significant size reduction can be obtained.

Figure 2 The six orientations of the SRR with respect to the k, E and H of the incident TEM field.

The magnetic resonance of the SRR depends on its orientation with respect to the external electric field E and the direction of propagation k, which implies six distinct orientations. In the first two cases (see a and b of Figure 2), in which the magnetic field E penetrates through the rings, the magnetic resonance of the SRR is excited by the magnetic field. The electric field can also excite the magnetic resonance when the incident wave penetrates through the rings and the external electric field. E is parallel to the split-bearing sides.⁵ However, when the external electric field E is rotated perpendicularly to the split-bearing sides, as in case c and d, no magnetic response is produced. In the other two cases, e and f, the external electric field E penetrates through the rings. No magnetic response is produced.

To account for the magnetoelectric coupling in Maxwell’s equations, the SRR metamaterials can be described by the constitutive relations.⁶

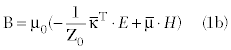
where and are the relative electric permittivity and relative magnetic permeability tensors and 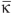is the magnetoelectric coupling dimensionless tensor. For different axes fixed to the SSR, only certain components and 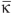tensors are of significance.

Considering a forward plane wave propagation of the form exp (iβz'), for the case 2c, which will be used in the following filter design.

So when ε_yy<0, the stop band will occur. Through a similar analysis, the other cases can be proved.

Design and Simulation

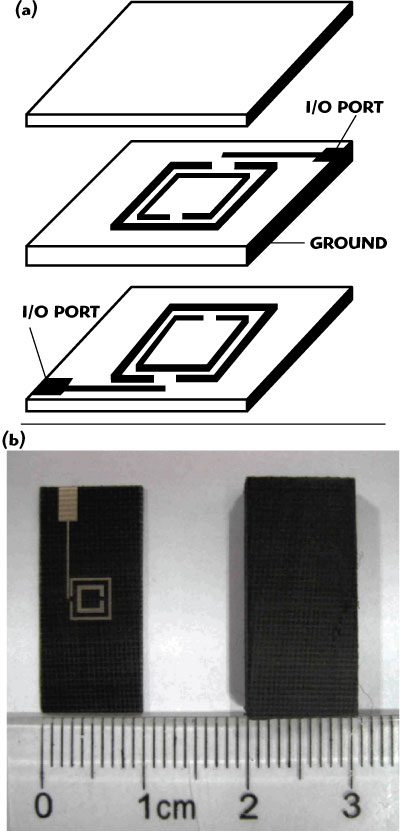
Figure 3 Structure of the two-pole SRR filter with skew-symmetric feed (a) and photograph of the filter (b).

Figure 3 shows the proposed filter, which is composed of three dielectric layers with the same relative permittivity 2.2 and two SRR layers embedded between the dielectric layers in the same plane, with splits laid in opposite directions. The most important innovation here is the ground that is located on the right and left sides, as shown. This design makes the external electric field E parallel to the split-bearing sides and makes sure that the magnetic resonance of the SRR takes place, in accord with the third case (c). The SRR filter, with skew-symmetric input and output feed-lines coupling on the first and last resonators, can generate two transmission extra zeros lying on either side of the passband because the delays in the upper path and the lower path are the same. The photograph of the fabricated filter is also shown in Figure 3b. The thickness of the first and third layers is 0.8 mm and the middle layer is 2.5 mm thick. The circuit dimensions are: r₀=2 mm, r_i= 1.3 mm, w₀=0.25 mm, w_i=0.4 mm, t= 0.45 mm, d₀=0.5 mm and d_i=0.4 mm. The width of the feed line is 0.2 mm. In the photograph, the left is the inner structure of the filter and at right is the whole structure.

Figure 4 Simulated and measured filter results.

The simulated and measured results are shown in Figure 4. From the EM simulation, the filter has a fractional bandwidth of 7 percent centered at 6.07 GHz, an in-band return loss of 20 dB and a minimum out-of-band loss of 25 dB. The transmission zeros are obtained near the passband at f₁= 5.49 GHz and f₂= 7.1 GHz. This structure can realize a good transmission characteristic and a compact size that is less than one third of the free space wavelength. From the measured data, two transmission zeros, at 5.53 and 6.96 GHz, are found in the passband response of the filter. Good agreement can be observed between the simulated responses and measured results.

Conclusion

In this article, the relationship between the magnetic resonance of an SRR and its orientation relative to the incident wave has been analyzed. A filter using two resonators has been successfully designed with a compact size, a low insertion loss and a sharp rejection loss. Furthermore, with the skew-symmetric feed structure, two transmission zeros can be achieved. Good agreement between measured and simulated data has been demonstrated.

Acknowledgment

This work was supported by the program for New Century Excellent Talents in University (NECT-04-0950).

References

1. W. Menzel, H. Schumacher, W. Schwab and X.K. Zhang, “Compact Multilayer Filter Structures for Coplanar MMICs,” IEEE Microwave and Guide Wave Letters, Vol. 2, No. 12, December 1992, pp. 497-498.
2. W.S. Tung, Y.C. Chiang and J.C. Cheng, “A New Compact LTCC Bandpass Filter Using Negative Coupling,” “IEEE Microwave and Wireless Components Letters, Vol. 15, No. 10, October 2005, pp. 641-643.
3. M. Shamonin, E. Shamonina, V. Kalinin and L. Solymar, “Properties of a Metamaterial Element: Analytical Solutions and Numerical Simulations for a Singly Split Double Ring,” Journal of Applied Physics, Vol. 95, April 1, 2004, pp. 3778-3784.
4. K. Aydin, I. Buly, K. Guven, M. Kafesaki, C.M. Soukoulis and E. Ozbay, “Investigation of Magnetic Resonances for Different Split Ring Resonator Parameters and Designs,” New Journal of Physics, Vol. 168, 2005, pp. 1-15.
5. N. Katsarakis, T. Koschny, M. Kafesaki, E.N. Economou and C.M. Soukoulis, “Electric Coupling to the Magnetic Resonance of Split Ring Resonators,” Applied Physics, Vol. 84, 2004, pp. 2943-2945.
6. C. Krowne, “Electromagnetic Theorems for Complex Anisotropic Media,” IEEE Transactions on Antennas and Propagation, Vol. 32, No. 11, November 1984, pp. 1224-1230.