The last two decades have witnessed the introduction of several new communication services that presented extraordinary challenges to microwave filter designers. Mobile communications cellular base stations and handsets require very tight electrical requirements to conserve precious frequency spectrum, miniaturization, large production volumes and low production cost. Filters for space applications in communications and broadcast satellite payloads have very challenging electrical requirements to be met under severe environmental conditions, high power handling, small mass and size. Millimetre-wave diplexers for Ka-band high speed multimedia Internet access satellite terminals pose challenging electrical requirements, very low production cost and large production volumes.
To meet these challenges, filter designers have developed design techniques, realization methods, new transmission media and innovative packaging configurations. The design techniques used circuit synthesis to obtain ideal optimum filter responses with finite real frequency transmission zeros for improved selectivity and complex transmission zeros to achieve group delay equalization. The ideal circuit models are then approximated by elements of transmission media (resonators and coupling elements) to construct a starting model of the microwave filter structure. Electromagnetic simulation and optimization is then applied to make the response of the realized microwave structures close to the idealized circuit response. The design procedures were vastly enabled by the availability of high speed computers, development of efficient electromagnetic simulation tools, numerical optimization techniques and innovative structures in various transmission media that enable realization of the optimal performance. Further, the models used in the simulation can take into account actual manufacturing details, such as finite milling tool sizes that can have major impact on the response. Once a final acceptable simulated response is achieved, the filters could be directly manufactured and its measured performance should be almost identical to the simulated response. This process largely eliminates the need for experimental tuning or repeated modification of the hardware, greatly reducing production cost and time.
This article presents a review of some modern filter design techniques, comparing these techniques with the well established design methods of more than four decades ago.1 The techniques are illustrated by several designs using different transmission media, including metallic waveguides, ridge waveguides realized in Low Temperature Co-fired Ceramics (LTCC) and dielectric loaded resonators.
Modern Filter Design Techniques

Figure 1 Flow chart for the filter design process.
Figure 1 illustrates the flow chart for modern filter design. From the given specifications, a circuit model is obtained in terms of a coupling matrix and input/output couplings. This process involves two steps. The first step is the solution of the approximation problem, which determines the order (number of filter poles) and the poles/zeros location of a transfer function that meets the given specifications. The second step is to synthesize a coupling matrix with a desired topology corresponding to a desired configuration. The lumped circuit model consists of resonant circuits coupled by frequency independent couplings,2 as shown in Figure 2.

Figure 2 General equivalent circuit model (normalized) for a microwave filter of order n, with cross-couplings among all the resonators.
Next, from the filter centre frequency, bandwidth, desired transmission medium in which the filter is to be realized, and coupling matrix element values, an initial set of physical dimensions are determined based on an electromagnetic model simulating the coupling between two isolated resonators. Figure 3 shows a simple example of how the iris dimensions are mapped to the circuit coupling values for a window between two rectangular or circular waveguide resonators.

Figure 3 Example of initial dimensions determination.
Once the complete filter physical model is generated, EM model simulation of the S-parameters is performed. In many practical cases, the EM simulation is carried out using the Mode Matching (MM) method,3 since it is computationally very efficient. However, depending on the complexity of the shapes and materials of the structure to be analyzed, other general numerical methods may be used such as the Finite Element Method, Finite Differences Time Domain Differences, etc., or hybrid combinations between them. Actually, there are many commercially available software packages that implement these techniques,4-8 even offering modules for dealing with high power effects (multipaction, passive intermodulation).9 They have an implicit trade-off between the structures that they are able to handle (complex shapes and material), computer resources (RAM memory, computation time, etc.) and accuracy.
Moreover, the response of the filter using the initial dimensions will usually be relatively poor, since the original design did not take into account the interactions among the resonators and the loading effects due to the multiple couplings. The simulated response is compared with the circuit model response, and an error or cost function is computed. Using an optimization routine, the dimensions of the filter are adjusted to minimize the cost function (see Figure 1). This process is repeated until the desired response is achieved.

Table 1 Comparison Between Design Steps "Now" and "Then"
It is interesting to contrast this modern design process with the techniques used four decades ago.1 Many of these designs are found in Reference 10. Table 1 summarizes the differences between what was used then and now. Although essentially the same design steps are employed, the major differences include:
- Use of advanced filter synthesis techniques
- Introduction of finite transmission zeros using the new coupling topologies employing the concepts of positive and negative couplings
- Use of full-wave simulators in powerful CAD tools
Choosing the transmission medium is one of the key issues in the realization of filters and multiplexers and its selection is related to many factors. An initial classification could be based on frequency range and would consider aspects such as physical size, unloaded quality factor Q, power handling capability, temperature drift and production cost.
Some transmission media and corresponding filter technologies include:
- The lumped element filters employed in the microwave range operate typically in hundreds of MHz’s (they can be used even at higher frequencies), with unloaded Q in the hundreds. Their dimensions must be much smaller than the operating wavelength and, thus, at high frequencies they are very difficult to manufacture with good performance. Hence, the distributed components (larger size) are used for higher microwave frequencies.
- Microwave filters implemented in air-filled rectangular waveguides, ridge waveguides and circular waveguides operating in their fundamental TE mode. For silver-plated resonators, unloaded Q factors of 10000 to 20000 can be achieved. Their insertion loss is low and they can handle higher power. However, they are usually bulky and their mass and temperature stability must be carefully considered in satellite applications. Aluminium can be used to reduce the weight. The temperature stability can be improved by an adequate design methodology, using special materials (e.g. invar) and smart mechanical structures to affect temperature compensation.11 Coaxial line filters can also be considered in the waveguide category, in this case operating in the TEM mode. They have higher losses and are common in wireless base stations and TV broadcasting.
- Planar structures are mostly employed for microwave integrated circuits (MIC) and monolithic microwave integrated circuits (MMIC). Microstrip lines, striplines, coplanar lines and suspended striplines belong to this category, whose main features are low cost and miniaturization. The power handling capability and Q factors (they can usually have Q fewer than 100) are usually very low, unless special materials are used.
- Dielectric resonator filters achieve higher unloaded Q (more than 40000 can be obtained) and very good temperature stability (temperature coefficient in the vicinity of one ppm/°C). A typical resonator is a ceramic cylindrical puck (where the electromagnetic field is mainly concentrated) suspended on a support within a metallic housing, operating in either single or hybrid modes. These filters have the disadvantages of close out-of-band spurious response, and relatively low power handling capability.
- LTCC technology is commonly used for designing compact filters. It is possible to integrate on the same substrate baseband/digital components together with RF miniaturized filters, active and passive devices.
- Other technologies used nowadays range from high temperature superconducting (HTS) components, surface acoustic wave (SAW) filters to micromachined electromechanical systems (MEMS), which cover a broad range of applications.
Examples of Modern Filter Design Techniques
This section presents examples of the application of modern design techniques to microwave and millimetre-wave filters and diplexers, ultra-wide band LTCC filters and dielectric resonator filters.
Millimetre-wave Filters and Diplexers
Diplexers are widely used in communication systems for reducing mass and volume of the required hardware. They enable use of the same antenna for different frequency bands, resulting in more compact systems. Their function is to separate the different bands of a signal into different ports. Alternatively, a diplexer combines two different signals with different spectral components into one common port.

Figure 4 H-plane T-junction diplexer: (a) block diagram; (b) diplexer configuration with asymmetric T-junction and two six-order channel filters with asymmetric inductive windows; and (c) diplexer performance.
A diplexer consists of a power divider and two channel filters, as shown in Figure 4. Electrical parameters that must be maintained over operating temperature range include: bandwidths of the channels and their separation, out-of-band rejection, insertion loss, in-band transmission and group delay responses flatness, power handling, low passive inter-modulation and multipactor effects. Mechanical packaging and geometrical characteristics play an important role in order to achieve compact designs. A general theory for diplexers and multiplexers synthesis can be found in this reference.12 Several configurations and design procedures have been studied in the literature for realizing the multiplexing function.13-15 Some usual multiplexer configurations with different numbers of channels in rectangular waveguide can be seen in Figure 5.

Figure 5 Rectangular waveguide multiplexer configurations: (a) diplexer made up of a stepped impedance low-pass filter and corrugated high-pass filter; (b) full H-plane diplexer; (c) E-plane divider and inductive windows filter with E-plane rounded corners; (d) full H-plane diplexer with H-plane rounder corners; (e) triplexer with E-plane rounded corners; and (f) manifold five-channel multiplexer.
Diplexer design starts with the channel filters, which must achieve the required channel performances before they are connected into the power divider. Then, two methods are usually followed to obtain the final device. In the first one, the channel filters are re-optimized within the diplexer environment, which includes the effects of the power divider discontinuities as well as the interaction between the channel filters. For the second method, the original channel filter designs are maintained and additional matching elements (as seen in Figure 4b) are incorporated into the power divider junction to obtain the required matching in the passbands. One of the main differences with the approach followed in the past is that these adjustments are done on the computer, and the diplexer that is manufactured already includes all the higher-order mode interactions within the structure.
Furthermore, other effects that are accurately taken into account are the round corners in the rectangular waveguides resulting from the finite radius tools in the manufacturing. At low frequency bands, this corner problem may not be serious, but it becomes critical for millimetre-wave frequencies, since the dimensions of the filter resonators are now comparable to the round corners. To overcome this problem modified models are used in the simulations, including the effect of the tool in the manufacturing (see for instance the different rounding in Figures 5c and 5d, related to different types of construction). Manufactured diplexers using such modified filter models have almost identical measured and simulated responses. The modified filters also allow the use of relatively large radius tools, which can reduce the manufacturing difficulty and cost.

Figure 6 Simulation and measurement of a five-channel manifold multiplexer in H-plane rectangular waveguide.16
Other additional considerations can be easily included in the simulations to reduce the production cost. For instance, the asymmetric inductive window filters shown in Figure 4b (instead of using symmetric irises as in Figure 5b) reduce to almost one half the path that a milling tool must cover in the production line (and thus the time and cost). All these considerations have been taken into account into the millimetre-wave diplexer in Figure 4c. Finally, it is important to adequately select the elements of the diplexer. Specifically for the power divider, E- or H-plane T-junctions are used for narrow to medium bandwidth applications. However, E-plane bifurcation is preferred for diplexers with broadband channels or with large frequency separation between channels. The manifold structures, where all the filters are connected to a main waveguide, are very common in contiguous band applications. An example is shown in Figure 6. All the channel interactions are considered in the full-wave analysis of the structure, as well as higher-order mode effects.
LTCC Ridge Waveguide Filters for Ultra-wideband (UWB) Applications

Figure 7 (a) Homogeneously dielectric-filled ridge waveguide with solid metallic wall; (b) LTCC implementation: the vertical solid walls of the ridge waveguide are approximated by a via fence.
Filters implemented in LTCC are very well suited for the integration with other microwave components on a multilayer stack-up substrate, reducing size and weight. This technology employs a multilayer substrate manufactured by deposition, layer by layer of dielectric and metallic patterns. This process allows the realization of three-dimensional transmission media (rectangular waveguides and ridge waveguides, for example), which can be used to obtain resonators with higher unloaded Q than planar structures. To realize waveguides in LTCC,17 the bottom and top walls are replaced by metallization layers. Via fences are incorporated to approximate the side conducting walls and the metallic housing, as shown in Figure 7 for the implementation of a LTCC ridge waveguide.
Ridge waveguides have low cut-off frequency and wide monomode range of the fundamental mode. They have larger size than planar filters, but they can provide lower insertion loss, wide spurious-free response and wideband performance.18 This LTCC approach may be seen as an intermediate alternative between metallic waveguides and planar circuits.

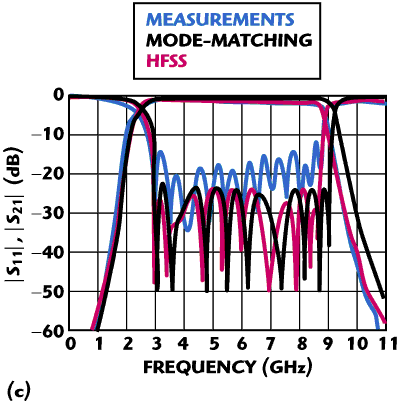
Figure 8 Theoretical and experimental results for the LTCC filter module in the fixture.20
Recently, UWB components and filters have gotten the attention of many researchers, with designs mainly focused on planar circuits.19 The structure presented in Figure 8 is an approach for realizing UWB filters based on LTCC.20 The module shown in Figure 8a is made up of a ninth-order ridge waveguide filter, designed for a passband from 3 to 9 GHz. It includes the input and output transitions to 50 Ω striplines used for the experimental evaluation of the filter. The whole LTCC module was built and a fixture designed to enable scattering parameter measurements. Figure 8b shows a photograph of the filter and the fixture.
The initial design of this structure is carried out assuming ideal solid metallic wall waveguides as in Figure 7a. Thus, the full-wave analysis and design of the waveguide structures can be obtained by MM in a very efficient way using the procedure discussed in the previous section. Before the manufacturing, the parasitic effect of the via fence and the losses is investigated with a general purpose tool such as HFSS.4 This part of the design is carried out when one feasible set of dimensions have already been obtained and, thus, the longer simulation times can be tolerated. The comparisons between the simulations and the experimental measurements are shown in Figure 8d, showing good agreement.

Figure 9 Simulated performance (mm and HFSS) for a LTCC ridge waveguide diplexer.
The same type of manufacturing concepts can be used to design wideband multiplexers.21 For instance, Figure 9 shows a diplexer designed for LTCC integration. Channel filter 1 and channel filter 2 are ridge waveguide filters based on the same approach as in Figure 7. The two filters are connected by a ridge waveguide power divider in E-plane configuration. The analysis and design of the diplexer is carried out by MM, and then is checked with HFSS. The responses are shown in Figure 9.
Dielectric Loaded Resonator Filters
The breakthrough in ceramic material technology, the significant progress in satellite communications in the late 80s and the rapid expansion of mobile communications in the 90s have revived interest in dielectric resonator (DR) applications for a wide variety of microwave circuit configurations and sub-systems.22,33 New high dielectric constant materials with high quality factor and low temperature coefficient were developed. The material can have the desired small controllable temperature coefficients over the useful operating temperature range. In addition, new filter configurations such as single and dual-mode filters with elliptic function responses were developed. These filters have the advantages of low loss, smaller size and superior temperature stability. A detailed review of the design and realization of several dielectric resonator filters can be found in Reference 22.
The TE01δ mode filter with planar layout offers many advantages over an in-line configuration and therefore it has been widely used in the base stations for mobile communication systems.26,33 TE01δ mode is the most commonly used mode in DR filters because it is the fundamental mode of the DR and it has no degenerate mode. As a result, TE01δ single-mode filters offer the advantages of design simplicity, flexibility in layout options and low-cost manufacturing. TE mode filters can have planar layout which is very suitable for mass production.

Figure 10 Basic building blocks of TE mode DR filter: (a) aperture coupled quadruplet; (b) probe coupled tri-section; (c) probe coupled quadruplet; and (d) probe coupled tri-section.
Non-adjacent coupling can be used to realize advanced filter features, such as quasi-elliptic function, constant delay and asymmetric responses. Quadruplet and tri-sections can be regarded as basic building blocks to generate symmetric and asymmetric transmission zeros. A non-adjacent coupling can be realized with quadruplet and tri-sections for TE mode cavities and their equivalent coupled-resonator model are shown in Figure 10,33 where magnetic coupling is regarded as positive coupling and denoted by an inductor. The non-adjacent coupling, which has opposite sign with adjacent coupling, is regarded as negative coupling and denoted by a capacitor. It is interesting to note that relative signs of the cross-coupling realized by an iris in a planar quadruplet and tri-sections are different, as is the cross-coupling by probe. The coupling property of the tri-section is also different from other commonly used types of cavities, such as waveguide and comb-line cavities because of the different field distributions of the resonator mode.
An example of a five-pole TE mode DR filter can be found in this reference.33 The filter used three non-adjacent aperture couplings including both inductive and capacitive couplings and achieved frequency response with three transmission zeros all at the lower side of the passband. The coupling matrix of this filter is:


Figure 11 Layout of the five-pole TE mode DR filter and the magnetic field orientation of the resonator.
The filter layout is shown in Figure 11. The orientation of the magnetic field near the cavities sidewall is also shown in Figure 11 to justify that the couplings M24(–), M25(+) and M15(–) are all implemented by coupling irises. The measured results are shown in Figure 12. This is an illustrative example of how new couplings and topologies are combined with improved materials to provide advanced filters.

Figure 12 Measured frequency responses for the five-pole TE mode DR filter.
Conclusion
This paper has illustrated some relevant aspects in the evolution of filter design methods in the last decades. Although the main theory remains very solid, a deep comprehension of filter concepts and the improvement of CAD tools have led to significant advances in the design techniques. In addition, there are many stringent specifications to be met in the applications demanded by the industry. High selectivity, group delay flatness, power handling, insertion loss or mass and volume constrains are some of the usual requirements that have to be fulfilled by a microwave filter. As a result, many technologies and physical configurations have been introduced and developed to satisfy the features needed in diverse applications. The achieved design advances have followed directions mandated by the industry to improve the features of the filters, reducing the cost and development time to market.
References
1. E. Tahan, “Microwave Filter Design Techniques,” Microwave Journal, March 1962, pp. 111-116.
2. A.E. Atia and A.E. Williams, “Narrow Bandpass Waveguide Filters,” IEEE Transactions on Microwave Theory and Techniques, Vol. 20, No. 4, April 1972, pp. 258-265.
3. G. Conciauro, M. Guglielmi and R. Sorrentino, Advanced Modal Analysis: CAD Techniques for Waveguide Components and Filters, John Wiley & Sons Inc., New York, NY 2000.
4. Ansoft High Frequency Structure Simulator (HFSS).
5. CST Microwave Studio.
6. Wasp-Net, Microwave Innovation Group.
7. Microwave Wizard, Mician GmbH.
8. Full-Wave Electromagnetic Simulation Tool (FEST 3D), European Space Agency ESA/ESTEC.
9. C. Vicente, M. Mattes, D. Wolk, B. Mottet, H.L. Hartnagel, J.R. Mosig and D. Raboso, “Multipactor Breakdown Prediction in Rectangular Waveguide-based Components,” IEEE MTT-S International Microwave Symposium Digest, Long Beach, CA, June 2005.
10. G. Matthaei, L. Young, and E.M.T. Jones, Microwave Filters, Impedance-matching Networks and Coupling Structures, McGraw-Hill Book Co., New York, NY 1964.
11. C. Wang and K.A. Zaki, “Temperature Compensation of Combline Resonators and Filters,” IEEE-MTTS, International Microwave Symposium Digest, Vol. 3, June 1999, pp. 1041-1044.
12. D. Rhodes and R. Levy, “A Generalized Multiplexer Theory,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-27, February 1979, pp. 99-111.
13. J. Uher, J. Bornemann and U. Rosenberg, Waveguide Components for Antenna Feed Systems, Artech House Inc., Norwood, MA.
14. H.W. Yao, A. Abdelmonem, J.F. Liang, X.P. Liang, K.A. Zaki and A. Martin, “Wideband Waveguide and Ridge Waveguide T-Junctions for Diplexer Applications,” IEEE Transactions on Microwave Theory and Techniques, Vol. 41, No. 12, December 1993.
15. Y. Rong, H.W. Yao, K.A. Zaki and T.G. Dolan, “Millimetre-wave Ka-band H-plane Diplexers and Multiplexers,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-47, No. 12, December 1999, pp. 2325-2330.
16. J.R. Montejo-Garai, J.A. Ruiz-Cruz and J.M. Rebollar, “Full-wave Design of H-plane Contiguous Manifold Output Multiplexers Using the Fictitious Reactive Load Concept,” IEEE Transactions on Microwave Theory and Techniques, Vol. 53, No. 8, August 2005, pp. 2628-2632.
17. A. Piloto, K. Leahy, B. Flanick and K.A. Zaki, “Waveguide Filters Having a Layered Dielectric Structure,” US Patent 5 382 931, January 17, 1995.
18. Y. Rong, K.A. Zaki, J. Gipprich, M. Hageman and D. Stevens, “LTCC Wideband Ridge-waveguide Bandpass Filters,” IEEE Transactions on Microwave Theory and Techniques, Vol. 47, September 1999, pp. 1836-1940.
19. L. Zhu, S. Sun and W. Menzel, “Ultra-wideband (UWB) Bandpass Filters Using Multiple-mode Resonator,” IEEE Microwave and Wireless Components. Letters, November 2005, pp. 796-798.
20. J.A. Ruiz-Cruz, Y. Zhang, K.A. Zaki, A.J. Piloto and J. Tallo, “Ultra-wideband LTCC Ridge Waveguide Filters,” IEEE Microwave and Wireless Components Letters, Vol. 17, No. 2, February 2007, pp. 115-117.
21. Y. Zhang, J.A. Ruiz-Cruz and K.A. Zaki, “Ridge Waveguide Divider Junctions for Wideband Multiplexer Applications,” 2006 IEEE MTT-S International Microwave Symposium Digest, June 2006, pp. 1225-1228.
22. C. Wang and K. Zaki, “Dielectric Resonators and Filters,” IEEE Microwave Magazine, October 2007, pp. 115-127.
23. K.A. Zaki and A.E. Atia, “Modes in Dielectric Loaded Waveguides and Resonators,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-31, No. 12, December 1983, pp. 1039-1045.
24. Y. Kobayashi and M. Minegishi, “Precise Design of a Bandpass Filter Using High-Q Dielectric Resonators,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-35, December 1987, p. 1156.
25. K.A. Zaki, C. Chen and A.E. Atia, “Canonical and Longitudinal Dual-mode Dielectric Resonator Filters without Iris,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-35, December 1987, pp. 1130-1135.
26. T. Nishikawa, K. Wakino, K. Tsunoda and Y. Ishikawa, “Dielectric High Power Bandpass Filter Using Quarter-cut TE01 Image Resonator for Cellular Base Stations,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-35, December 1987, pp. 1150-1155.
27. C. Kudsia, R. Cameron and W.C. Tang, “Innovations in Microwave Filters and Multiplexing Networks for Communications Satellite Systems,” IEEE Transactions on Microwave Theory and Techniques, Vol. 40, June 1992, p. 1133.
28. R.V. Snyder, “Dielectric Resonator Filter with Wide Stopbands,” IEEE Transactions on Microwave Theory and Techniques, Vol. 40, November 1992, pp. 2100-2102.
29. J.F. Liang, K.A. Zaki and A.E. Atia, “Mixed Mode Dielectric Resonator Filters,” IEEE Transactions on Microwave Theory and Techniques, Vol. 42, December 1994, p. 2449.
30. C. Wang, H.W. Yao, K.A. Zaki and R. Mansour, “Mixed Mode Cylindrical Planar Dielectric Resonator Filters with Rectangular Enclosure,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-43, December 1995, pp. 2817-2823.
31. H.W. Yao, C. Wang and K.A. Zaki, “Quarter Wavelength Ceramic Combline Filters,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-44, December 1996, pp. 2673-2679
32. D. Kajfez and P. Guillon, Dielectric Resonators, Second Edition, Noble Publishing, 1998.
33. J.F. Liang and W.D. Blair, “High-Q TE01 Mode DR Filters for PCS Wireless Base Stations,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-46, December 1998, pp. 2493-2500.
Jorge A. Ruiz-Cruz received his Ingeniero de Telecomunicación degree in 1999 and his PhD degree in 2005, both from the Universidad Politécnica de Madrid, Spain. Since 1999, he has collaborated with the Grupo de Electromagnetismo Aplicado y Microondas at UPM. Before starting his PhD program, he was with RYMSA (2000). He is currently an assistant professor at the Universidad Autónoma de Madrid, Spain.
Chi Wang received his BSc (Eng) and MSc degrees from Beijing Institute Technology, China, in 1983 and 1986, respectively, and his PhD degree in 1997 from the University of Maryland. He is currently with Orbital Sciences Corp., Dulles, VA, as a program director.
Kawthar A. Zaki received her BS degree from Ain Shams University, Cairo, Egypt, in 1962, and her MS and PhD degrees from the University of California at Berkeley in 1966 and 1969, respectively, all in electrical engineering. In 1970, she joined the University of Maryland, where she is currently professor emeritus of electrical and computer engineering.
