Also, the channel gain can be expressed as the reciprocal of loss as shown in Equation 32:
Assuming the ith stage of a cascaded system represents the channel, then the signal power out of the channel, Psignal,i, is derived in Equation 33:
Here Psignal,i-1 corresponds to the output power of the transmitter PTX, Psignal,i equates to the signal power out of the channel and is applied as input power at the receiver, PRX. Consequently, the non-signal power Pnon-signal,i within the channel represents the amount of transmitted power not successfully received out of the channel (e.g., channel loss or path loss) which is additive wasted power of the channel which is a component of the cascade between source and sink and this can be formulated as Equation 34:
Figure 4 Homodyne transmitter with a matched load.
where (1-Gchan) quantifies the proportion of the signal power lost due to various factors such as attenuation, scattering and absorption. Multiplying (1-Gchan) by Psignal,i-1 yields the amount of power dissipated during transmission and is the power lost or wasted in the channel. The waste factor for the channel can readily be calculated using Equation 34 to get the results of Equation 35:5-7
Notably, unlike electrical devices, a wireless channel does not have a non-path power component (Pnon-path), making it like a passive attenuator. Therefore, the waste factor for a channel (Wchan) is equivalent to that of a passive attenuator (Wchan=Lchan).
Waste Factor for a Homodyne Transmitter
The section presents a waste factor application example to compare two cascaded systems with different components. We compare the power efficiency of two different homodyne transmitters, each with matched load termination at the antenna. Figure 4 shows the homodyne transmitter block diagram.
Table 3 illustrates the application of the waste factor (W) and the value of W for a cascade as described in Equation 5 and Equation 13 to evaluate the impact of overall energy efficiency using different components in a homodyne transmitter system.
Table 3 and Figure 4 are illustrative for how to use W to characterize energy efficiency based on the selection of different components. Using Case 1 as an example, the waste factor of the homodyne transmitter based on component parameters in Table 3 is calculated using Equation 5 or Equation 24 and W = 1/ηw.

Example 1 in Table 3 compares Case 1 and Case 2 to show how components with different efficiencies impact W of the cascade using Equation 5 or Equation 24. It can be seen that Case 1, with a more efficient RF amplifier, results in a lower W of 2.20 (3.42 dB), signifying better power efficiency and less wasted power than Case 2, which uses a less efficient RF amplifier and yields a larger W of 4.12 (6.15 dB) for the cascade. Example 1 shows that almost twice as much power is wasted in Case 2 (e.g., 6.15 dB – 3.42 dB = 2.73 dB) which is roughly the proportion of efficiencies of the two different final amplifiers. The above example shows that amplifier efficiency closest to the sink dominates the overall waste figure of the cascade.
In Example 2 of Table 3, Cases 3 and 4 are considered. Here, again, overall W, as computed in Equation 5 or Equation 24, is impacted by specific components, but for this example, we see that components farthest from the sink have much less impact on overall power efficiency. Case 3 shows how a baseband amplifier that is much more power efficient achieves only a slightly lower W of 3.39 (5.30 dB) compared to Case 4, which uses an identical RF amplifier but a much less efficient baseband amplifier. Case 4 has only 0.09 dB poorer energy efficiency with a W of 3.46 (5.39 dB). While these observations are intuitive, waste factor allows precise quantification and comparison.
These examples illustrate the importance of optimizing power efficiency in the components closest to the sink to reduce waste and enhance system efficiency. These examples also show how waste factor may assist researchers and engineers in creating energy-efficient component technologies and system designs.
Waste Factor for a Communication System with a Channel

Figure 5 A communication system including a channel.
Figure 5 shows a system with a channel that is easily treated as a cascaded system. Note that P1 is the power from the TX, P2 is the power out of the channel and into the RX, and WTX and WRX represent the waste factors of the TX cascade and RX cascade (not shown), respectively. Note that the channel may be wireless, wired, acoustical, optical, etc. and may have multiple users/links.
The total waste factor for the cascaded system, including the TX and RX components as well as the inherent loss of a channel, is defined as Wsys. Using Equation 5 or Equation 24, Wsys is given by Equation 36 as:
From Equation 35, it is clear that Wchan=Lchan and when the receiver gain, GRX, is substantially less than the loss of the channel, Lchan, which is typical for wireless links, Wsys in Equation 36 then simplifies to Equation 37:5,6,7
Equation 37 implies that to achieve a smaller Wsys value, which is indicative of a more power-efficient end-to-end system, it is essential to have high-gain receivers, and transmitters with high power efficiency.
The key result of Equation 37 may be written in dB as Equation 38:

Equation 38 shows that the strategic configuration of power-efficient TX output components and high-gain receivers minimizes energy waste over any channel, optimizing the system energy efficiency. The simplicity of the system depicted in Figure 5 underscores the need for certain components to be properly designed for greater power efficiency to have the greatest impact on the overall minimization of power waste and offers a framework for understanding mobile system power consumption for individual users.
Now investigate how waste figure varies for different communication systems comprising a simplified TX, a lossy channel and a RX. The assessment considers the system architecture of Figure 5 while varying system gain and efficiency at each stage as shown in Table 4. This comparison enables an intuitive understanding of how changes in system gain and efficiency impact the overall energy efficiency of the communication system in Figure 5.
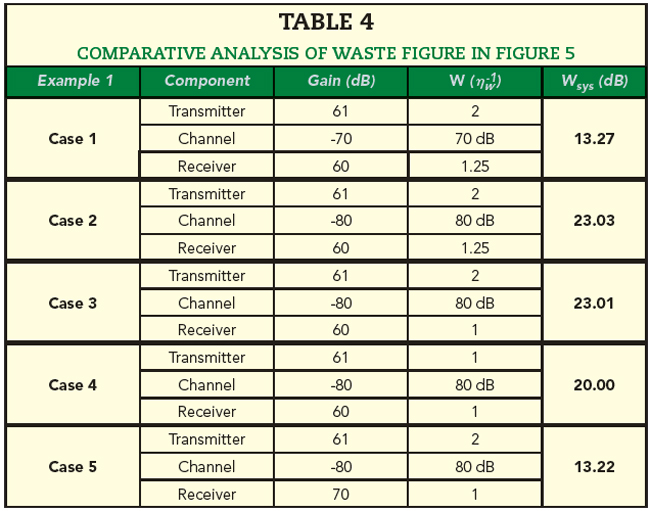
The different cases in Table 4 illustrate that when the channel loss increases, as seen between Case 1 and Case 2, the waste figure increases by a similar amount (e.g, the channel loss dominates power efficiency). Case 3 shows that making the RX more efficient (e.g., increasing its efficiency by 25% from 0.8 to 1), does not significantly affect the waste figure, reducing it by only 0.02 dB. However, in Case 4, when the TX efficiency is improved (e.g. doubled) from 0.5 to 1 with all other parameters the same as in Case 3, there is a noticeable decrease of 3 dB in the waste figure, which is equal to the increase in TX efficiency. This design saves half the consumed power for the same link quality. Case 5 uses the setup of Case 3 with the RX system gain increased from 60 to 70 dB. This saves much more power with the waste figure dropping by 10 dB. Comparing Case 5 and Case 3, Case 5 is vastly more energy efficient. By increasing the RX system gain, Case 5 needs only one-tenth the TX power compared to Case 3 for the same cascade output power. This efficiency is shown by a 10 dB reduction in the waste factor, indicating that Case 5 uses energy 10 times more effectively than Case 3.
The conclusion from these observations is that if a lower loss channel is not available, increasing the RX gain has a significant impact on reducing waste. Additionally, improving the efficiency of the TX is also a vital way to make the system more power efficient. The waste figure theory was first tested for the power consumption tradeoff between a single hop communication system versus a relay system, whereby operating regions were found that indicated which architecture was more power efficient to use for an end user.7
Waste Factor Applied to Data Centers
Data centers are one of the largest consumers of power today. The information technology (IT) field has established the power usage effectiveness (PUE) FoM.8 Employing the PUE to determine the power usage of non-IT components in relation to servers in a data center offers a straightforward approach to associating non-IT power consumption with the power consumed by server operations.
The IT industry defines PUE as the ratio between the summation of the amount of energy consumed by IT equipment and the energy consumed by auxiliary equipment for data operations, compared to just the IT equipment energy usage. As shown in Equation 39, the IT equipment includes networking equipment that is on the signal path, (e.g., switches, routers, firewalls, etc.) as well as components that do not transfer data but that are vital to data processing and thus may be considered as being on the cascade (using the waste factor model of Figure 1) but as not contributing (e.g., wasted power in the transport of information in servers, storage systems, etc.). The energy consumption of auxiliary equipment includes cooling, lighting and non-network devices that do not carry data center information, etc., and are similar to non-path components in the waste factor model (e.g. see Equation 9)4,8


