Oven controlled crystal oscillators (OCXOs) are deployed in a variety of applications where the g-sensitivity of piezoelectric crystals plays a significant role in the overall system performance. These devices are used in communication, navigation, timing, radar and quantum computing applications to generate high spectral purity and stable primary frequency references. Developing new techniques to mitigate and minimize OCXO frequency source degradation is critical to advancing the state-of-the-art sensitivity and accuracy demanded by rapid technological advancements across scientific, commercial and defense industries. This article will present an oscillator that achieves a significant reduction in the dynamic phase noise of a compact crystal oscillator.
Equipment operating in the aerospace environment can experience any number of challenging dynamic vibration environments with a range of intensities and frequencies. These vibrations have many causes. They may arise from aircraft features like propellers, jet engines or rotors. The vibrations may also be the result of interaction with the atmosphere in response to turbulence and maneuvers. They may also be caused by terrestrial operations like take-off, landing or launch and finally, there may be extra-terrestrial micro vibrations while the platform is in orbit. The phase noise degradation experienced in these environments can range from micro-vibration levels experienced in a spacecraft due to altitude or spin thruster controllers to vibration levels as high as 0.02 g2/Hz with grms = 4.4 g. Regardless of the magnitude of the vibration, OCXO degradation can easily cause system degradation.
The effects of vibration are also influenced by the location of the equipment, whether it is inside or outside of the aircraft, along with how the equipment is sheltered. The equipment itself can also contribute to the vibration profile because of its mass, materials or mechanical components, such as cooling fans. Dynamic vibration degradation created by the environments just described will typically manifest in the OCXO output as a frequency shift, elevated spurious signal levels and higher phase noise. As the OCXO performance degrades, radar range resolution, navigation receiver performance or electronic warfare system performance may also degrade.
OCXOs can also provide good short-term stability and clean frequency references for atomic frequency standards, whether the standards use Rb,1 Cs or Hydrogen maser atomic clocks.2 By locking the OCXO reference to atomic resonance, the short-term stability of the reference is combined with the long-term stability of the atomic resonance. This stability enables the fundamental laws of physics to be tested in settings that require extreme levels of precision and accuracy.
In the Square Kilometer Array (SKA) and next-generation Very Large Array (ngVLA) radio astronomy science projects, the precise time and frequency distribution is of significant concern. In the SKA project, an H-maser clock needs to be distributed by fiber and then recovered at each dish site to achieve the required frequency stability and phase noise performance. This synchronized frequency signal needs to be distributed to hundreds of receivers in a star-shaped topology. To support astronomical observations, the coherence requirements demand short-term phase stability of better than 1 × 10-12 at τ = 1 sec intervals.3 High-stability, phase-locked OCXOs are required between H-masers at transmit and receiver sites.
Similarly, autonomous vehicles that use frequency-modulated continuous wave radars present challenges. The frequency accuracy and stability of the reference clocks play essential roles in determining the accuracy and probability of moving target detection.4 Unless vibration-induced noise caused by road conditions, vehicle acceleration or braking is accounted for, the vibration-induced noise can create OCXO frequency or phase shifts and this will likely degrade the performance of the vehicle’s radar receiver.
ACCELERATION-INDUCED CRYSTAL OSCILLATOR PHASE NOISE
It is well-known5 that when a crystal oscillator of frequency, f0, is subjected to random acceleration, its resonant frequency shift, Δf, is proportional to the magnitude of acceleration and dependent on the direction of that acceleration. This frequency shift can be written as a vector dot product as shown in Equation 1:

where  and
and 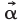 are the acceleration sensitivity and the peak applied acceleration vectors, respectively.
are the acceleration sensitivity and the peak applied acceleration vectors, respectively.
As a result, the associated single sideband (SSB) power spectral density of phase fluctuations, expressed in dB, can be determined as in Equation 2:
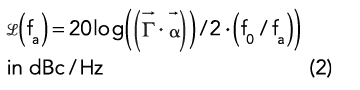
MITIGATION OF OSCILLATOR VIBRATION
Over the past 40+ years, Quantic Wenzel has developed a variety of methods to counteract vibration-induced signal degradation. Traditional techniques such as crystal selection, passive mechanical isolation and bootstrapping have become mainstays in low phase noise designs for dynamic environments. Quantic Wenzel’s latest developments in active vibration compensation, when used alone or in combination with traditional techniques, are enabling further improvement in the state-of-the-art phase noise performance during vibration.
A standard approach to mitigate the effects of vibration-induced phase noise in oscillators is to use passive mechanical dampers or isolators that have a low natural frequency. Examples of this technique include wire rope isolators and compounded elastomeric shock mounts. Depending on the quantity and damping characteristics of the isolators and shock mounts, the size of the oscillator package may increase.
Additionally, the resonant frequency of the vibration-isolated mass can introduce signal degradation. To mitigate this effect, Quantic Wenzel has devised a modular payload system that can adjust this resonance using different combinations of base metals, shock mount configurations and extra masses.
However, active vibration compensation enables real-time detection and compensation of crystal acceleration sensitivity over a wider range of vibration frequencies. Quantic Wenzel has developed analog and digital active compensation techniques to address these active vibration-compensation challenges. These techniques are being implemented across a wide range of induced environmental conditions. They enable the selection of an optimal solution that accommodates size, weight and power considerations.

