Integrated circuits have redefined electronics in many areas, but not microwave filters until recently. Bringing the power of MMIC fabrication technology to bear on filtering applications has inspired the development of new tools and new ways of thinking about classic problems. This article discusses advancements in software tools and filter hardware, along with applications where both are valuable.
TOOLS OF THE TRADE: THE MMIC FILTER SOFTWARE STACK
In contrast to most broadband components, fixed filters are generally custom-designed for a system with sometimes vaguely defined performance specifications that may shift frequently. Increasingly, customer requirements are driven more by size than rejection requirements. Frequently, filters solve an unanticipated design problem, often stemming from the frequency plan or previous component choices. The filter business and manufacturing process require speed at every step. Once specifications are agreed upon, the design, fabrication and characterization of the filter must happen quickly. However, since fixed filters are passive and linear, the characterization consists of measuring a single two-port S-parameter. To address this new paradigm with maximum speed, new tools are required. Software tools that automate key steps in the design and commercialization processes are necessary to prevent repetitive and time-consuming work.
Step 0: Theoretical Definition with LC and Microstrip Filter Design Tools
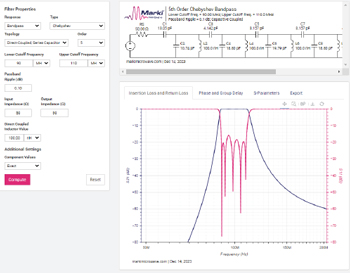
Figure 1 Fifth-order Chebyshev bandpass filter synthesis.
Before initiating a MMIC filter design, filter designers investigate what is theoretically possible and what kind of inductances and capacitances are necessary to realize these filters. Marki Microwave does this with analytical filter design tools that the company has made publicly available. The LC filter design tool uses equations from fundamental filter research to calculate the theoretical performance of many different types of filters (Chebyshev, Butterworth, Elliptical, etc.) of different orders at given cutoff frequencies. A representative output of this design tool is shown in Figure 1.
The microstrip filter design tool goes a step further and calculates the actual layout of a planar microstrip filter in a more limited number of topologies (Chebyshev and Butterworth). It calculates the scattering parameters for this structure using mathematical models. Tools like these allow a designer to quickly develop an intuition for what is possible in the filter space.
While powerful and fast, the drawback of these tools is that they only provide theoretical results. When fabricated, the filters created by the microstrip and LC filter design tools will not match the design tool results. The design tools do not account for parasitics of the inductors and capacitors, loss in the components and transmission lines and especially, coupling between different structures. The real-world performance of the filter will not match the simplistic simulation. To achieve better results, further design optimization in a more realistic circuit solver is necessary. For optimal performance, retuning with a sophisticated circuit solver may be required.
Step 1: Topology Definition
Once the theoretical possibilities are understood, the next step is to find the best physical layout to implement in a MMIC structure. This requires researching previously published filter designs, experimenting with different coupling structures and possible circuits in a schematic-level circuit solver, along with exploring different implementations of the circuit in a 3D finite element method (FEM) electromagnetic solver. While standard optimization tools can be used, this is mostly a manual, analog process. The result of this process is not a specific filter design, however, but a topology. A filter topology is the essential, scalable geometry of a filter circuit implemented in a MMIC structure that can be scaled and re-optimized to change the center frequency and bandwidth while maintaining the basic artwork. A given topology will have 10 to 20 design variables that can be continuously varied, leading to millions of potential geometries. Only a small number of these geometries yield a useful filter. Beyond a specific constrained solution space of these design variables, the design is not viable due to unmanufacturable geometries or unacceptably high unit-to-unit variance. Within that useful filter range, however, many designs can be realized with first-pass success.
Step 2: Automatic Design

Figure 2 Filter topology matrix.
To realize a specific filter geometry, a designer starts with the base topology and a rough calculation to estimate a seed value for the 10 to 20 design variables. The designer then solves using the seed values in 3D and takes the output to iterate closer to the optimal filter design. This iterative process uses a combination of software tools to refine initial estimates.
Marki uses HOTMESS, a combination of an automatic 3D filter optimizer and a proprietary machine learning algorithm, to automate and optimize the process of creating a set of filters to meet requirements. There are two keys to this tool:
- The 3D FEM solver is relatively slow, taking minutes to hours to solve, so automating the process allows around-the-clock optimization of filters.
- The optimization routine is not blind. It uses the “incorporating prior knowledge” machine learning concept. Unlike a simple gradient solver, HOTMESS solves for the required circuit effect first, improving with each cycle.
Due to these properties, HOTMESS can solve for every achievable percentage bandwidth and center frequency for a given filter topology. Figure 2 illustrates that a filter design should more appropriately be thought of as a matrix of center frequency and passband combinations.
Step 3: Design a Filter Instantly
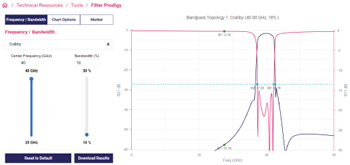
Figure 3 Prodigy™ Filter Designer user interface.
HOTMESS can provide a solution for nearly every filter topology, but this only addresses the design aspect of the problem. To address the manufacturing aspect, HOTMESS is paired with Prodigy™ Filter Designer to arm filter designers with as much information as early as possible before they develop a filter procurement specification. The publicly available Prodigy™ Filter Designer allows a user to design a filter at any center frequency and bandwidth within the operating range of a given topology. The Prodigy™ Filter Designer interface is shown in Figure 3.
In the Prodigy™ Filter Designer interface, a user selects the desired filter topology, center frequency and bandwidth. The interface then shows an insertion loss and return loss simulation for the selected filter design. This interface is very similar to the LC filter and microstrip filter solvers described earlier, but the underlying math is very different.
In contrast to the ideal filter prediction given by the mathematical models, Prodigy™ Filter Designer creates a real filter, with known design variables and size. Most importantly, Prodigy™ Filter Designer uses machine learning to calculate the real S-parameters of the filters with all the effects like metal loss, parasitics and cross-coupling. This design and its Touchstone file are immediately available to system designers so they can incorporate actual filter performance at the initial stages of a system design.
While Prodigy™ Filter Designer can display every achievable filter for a given topology, it does not display the best achievable performance for a given filter specification. Where the performance of the filter is sufficient, the Prodigy solution will be a cost-effective solution. When the Prodigy solution does not meet the requirements, there are trade-off techniques among rejection, size and insertion loss that can be considered.
Step 4: Optimize Cost and Prototyping Speed
Since implementing these new MMIC filter models that allow filter designs to be developed quickly and at scale, the library of in-stock filter designs at Marki has grown quickly. This can be seen in Figure 4. The anticipation is that there will be hundreds of filter designs in production by the end of 2024.
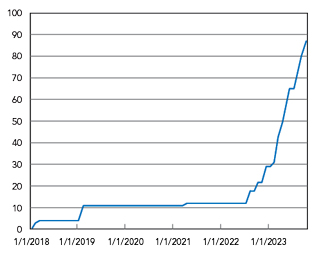
Figure 4 Marki MMIC filter catalog.

Figure 5 Filter search tool and the results.
Since each filter has its unique combination of center frequency and rejection shape, finding the optimum filter for a given requirement becomes challenging. This challenge is further compounded for applications that need a series of filters for harmonic cleanup or switched filter banks. A filter search tool has been developed to address this issue. A user inputs passband and rejection performance requirements and the filter search tool cycles through all available catalog products and displays the best match. If no filter is found that meets the desired specifications, the closest available match can be found using the “partial match” match option. While the type (lowpass, highpass or bandpass) of filter can be a selection criterion, leaving this option generic can expand the pool of possible solutions. Figure 5 shows the user interface and the output of the filter selection search tool.
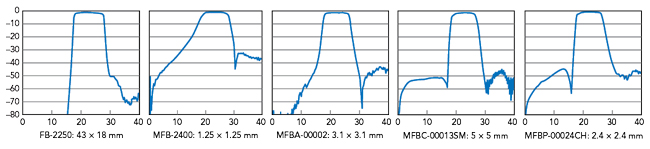
Figure 6 Filter trade-offs affect performance.
FILTER APPLICATIONS

Figure 6 shows the performance of filters with a similar center frequency and bandwidth, but different trade-offs in terms of size, insertion loss, close-in rejection and far-out rejection. The first result in Figure 6 is a legacy laminate filter in a connectorized module and the rest are MMIC filters released after 2020. Each of the MMIC filters utilizes a new topology developed to meet a new system requirement. Table 1 shows selected characteristics of the filters in Figure 6.

