Switched Filter Banks
Switched filter banks (SFBs) are a common application for MMIC filters. An SFB is commonly found in wideband receivers and wideband LO generators and synthesizers. MMIC filters are particularly well suited for use in SFBs for two reasons. First, SFBs use many filters, so the size advantage of a MMIC filter is multiplied by the number of filters in the bank. A reduction of 100 mm2 on a single filter translates to a size reduction of 8 cm2 on an 8-channel SFB and that is significant. Secondly, the cost of creating a new MMIC filter is dominated by the mask for the reticle and the first wafers. Mask production is a slow, serial and expensive process performed with electron beam lithography. Since four to eight filters can share a single mask, the major cost of developing the filters is split among the entire bank of filters.
The most straightforward application of MMIC filters for SFBs is the filtering of harmonics following a frequency multiplication block. Figure 7 shows the lineup for an SFB after a frequency doubler, along with the placement of the filters. With applications going higher in frequency, the multiplication block could be a doubler, tripler or quadrupler.

Figure 7 SFB in a transmit lineup.
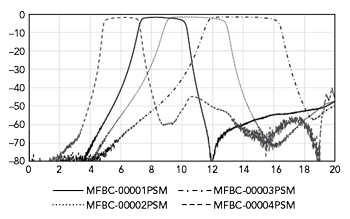
Figure 8 Retuning filter designs for different bands.
Marki doublers achieve harmonic suppression performance of 40 to 60 dBc across several octaves of bandwidth, however, this performance may not meet the requirements of high performance electronic warfare and instrumentation LO generators. Because the harmonic spurs are always separated from the desired tone by a fixed ratio and not a fixed frequency, a constant percentage bandwidth filter bank is required. Fortunately, this design is straightforward in a MMIC filter using a single filter topology since the basic design can be scaled and retuned to move the center frequency as shown in Figure 8.
Pre-selection Filter
The pre-selection filter is another common SFB application. This function appears at the front end of a wideband receiver as shown in Figure 9. These filters typically come after the limiter and low noise amplifier (LNA) or they may be switched with the LNA to reduce the nonlinear harmonics created by the signal before frequency conversion or further signal processing. While these pre-selection filters can be constant percentage bandwidth when second-order intermodulation distortion (IP2) is a major limitation, frequently they are a fixed bandwidth to maximize the Nyquist zone of the ADC at the end of the receive chain. Figure 10 shows a series of four GHz filters that can be combined with SP4T switches on either side to create a four-channel 2 to 18 GHz pre-selection filter. While constant percentage bandwidth filters can easily be realized as MMICs by scaling the circuit, constant bandwidth filters offer a different set of challenges. This is particularly evident at low frequencies where filter bandwidths can be more than an octave. The performance of this 2 to 18 GHz pre-selection SFB is shown in Figure 10.
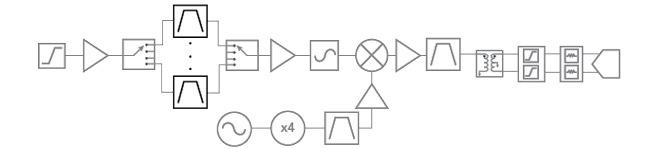
Figure 9 SFB used as a pre-selection filter.
CASCADING FILTERS
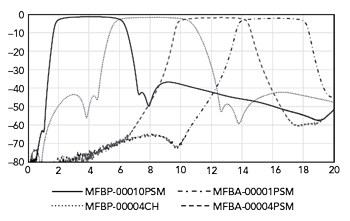
Figure 10 2 to 18 GHz SFB performance.
A solution for multi-octave filters is to cascade lowpass and highpass filters. This sounds straightforward, but not all filters can be cascaded and maintain satisfactory performance. A key attribute to success is ensuring that the lowpass and highpass filters have good out-of-band performance. Lowpass filters must have good high frequency response, which means a flat passband. Highpass filters must have good out-of-band performance, maintaining good rejection out to 40 GHz and beyond without bandpass filter reentrant mode issues.
There are several advantages to creating bandpass filters from highpass/lowpass filter combinations. The technique allows for arbitrarily wide percentage bandwidths, making 2 to 18 GHz filters as easy as 2 to 6 GHz filters. The highpass and lowpass filters can be designed and optimized independently, allowing for rapid design of a complete set of filters at regular steps. Lumped elements can be used in MMIC highpass and lowpass filters, allowing for a small die size. In theory, the combination highpass/lowpass filter can be in separate, well-matched packages placed close to each other.
However, not all filters can be cascaded. This technique is useful for improving the rejection of bandpass filters. When a requirement calls for a steeper rejection than a single filter can provide, a cascade filter may be the solution. However, precautions need to be taken because bandpass filters are reflective. This and other challenges can be addressed with reflectionless filters.
REFLECTIONLESS FILTERS
Classic filters function as mirrors outside of the passband. This may present an issue for frequency conversion functions like mixers, doublers and nonlinear transmission lines (NLTLs) because the strongest tone, (the LO, image or the fundamental input) is not the desired tone. Reflections of these high-power tones back into a frequency conversion device may cause unpredictable responses due to nonlinearities in the device. There are at least two solutions that may be appropriate for these issues. The best choice will depend on the specifics of the application:
Terminated Diplexers: A diplexer is a device that routes signals to specific output ports based on frequency. A bias tee is a simple and extreme example of a diplexer; most diplexers have a higher crossover frequency. When one side is terminated in a 50 Ω load, it will function as a highpass or lowpass filter where the common port has good return loss across the band. The diplexer design will determine the return loss performance of the highpass and lowpass ports. This approach can be an excellent termination for an NLTL or other multiplier chain since the low frequency fundamental tones can be eliminated. Figure 11 shows a block diagram of a diplexer terminating an NLTL to reduce reflections.
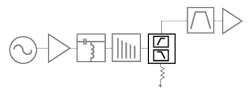
Figure 11 NLTL terminated with a diplexer.
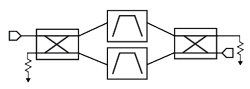
Figure 12 Balanced filter block diagram.
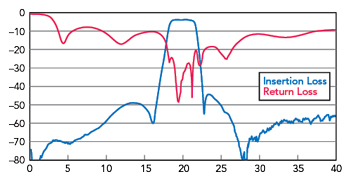
Figure 13 MFQH-00001CH performance plots.
Balanced Filters: To create a reflectionless, balanced circuit requires two identical subcircuits connected with quadrature hybrids. By combining MMIC filter technology and quadrature hybrid designs, designers can create reflectionless bandpass filters with good return loss across a wide bandwidth. The major benefit of this technique is that it is simple and can be realized on a single chip, with only a slight increase in chip area. The block diagram of this design approach is shown in Figure 12 and Figure 13 shows the actual performance of a Marki MMIC reflectionless bandpass filter.
VARACTOR-TUNABLE FILTERS
The ideal solution for many RF systems has long been tunable filters. If an ideal tunable filter were available, it would dramatically reduce the complexity, size and cost of many RF systems. There are many types of tunable or switchable filters available using various techniques. Varactor-tuned filters use fixed inductors with varying capacitors to move the values of the resonators. While these filters have found wide acceptance, tunable bandpass filters are only capable of fixed percentage bandwidth tuning, which creates challenges. Also, the return loss of varactor-tuned filters tends to suffer across the tuning range due to the detuning of the filter structures.
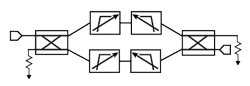
Figure 14 Varactor-tunable bandpass filter.
To overcome these limitations, many of the previously described techniques can improve the state-of-the-art in varactor-tuned filters. Marki solves the challenge of fixed percentage bandwidth tuning by designing separate highpass and lowpass filters that are tuned independently. Without these separate, independent tuning voltages, the best result is roughly fixed percentage bandwidth filters.
To overcome the challenge of detuning filters that degrade return loss, Marki designers embed a highpass/lowpass cascade in a balanced structure to provide good return loss regardless of the tuning state. This approach results in a versatile and effective filter for size-constrained applications that can sacrifice some rejection and insertion loss performance. Figure 14 shows the block diagram of this varactor-tunable bandpass filter approach.
The following charts show the performance of Marki’s MFBT-00003PSM varactor-tuned bandpass filter and they illustrate some of the concepts previously discussed. Figure 15a and Figure 15b show the insertion loss as the independent control voltages are swept. Figure 15c and Figure 15d show insertion loss for constant percentage bandwidth and constant bandwidth applications. Figure 16 shows the return loss for different bias conditions.
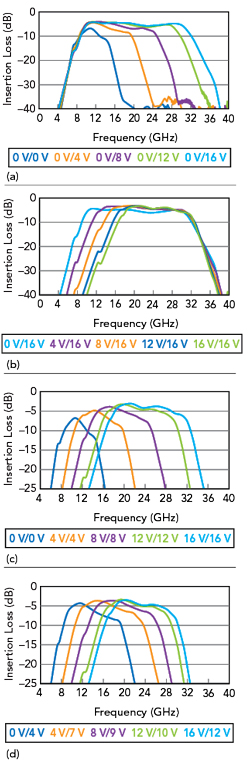
Figure 15 (a) Insertion loss sweeping lowpass. (b) Insertion loss sweeping highpass. (c) Insertion loss constant percentage bandwidth. (d) Insertion loss constant bandwidth.
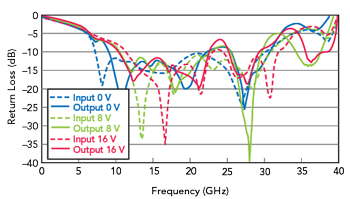
Figure 16 Insertion loss constant bandwidth.
CONCLUSION
Size and channel density requirements for high performance RF circuits pressure designers to minimize the footprint without sacrificing performance. When size is the primary concern, MMIC fixed and tunable filters offer significant size reductions and improved economics for applications where multiple filtering states are necessary. Innovation from companies like Marki in both automated design flows and filter performance enables a viable business model for high performance MMIC filters in the low volume and high-mix market applications.

