When we port tune the EM model we can find a set of tunes that meet the rejection goal in the upper stopband, but the transmission zeros in the lower stopband are not distinct and rejection is compromised (see Figure 15). The low side transmission zeros disappear. If we model the capacitive probe carefully the network theory model agrees with the EM simulation.
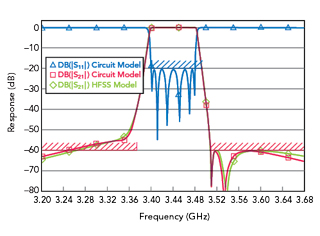
Figure 15 EM model port tuned to match upper stopband goals. The low side transmission zeros disappear.
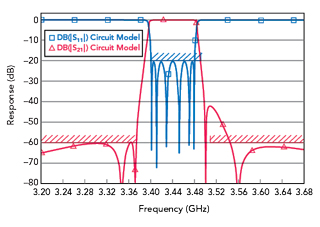
Figure 16 EM model port tuned to match the lower stopband goals, showing the upper stopband no longer meets the specification.
Likewise, we can find a different tuning that meets the rejection in the lower stopband, but now the rejection in the upper stopband does not meet the specification (see Figure 16).
We conclude that there is no tuning solution that actually meets the symmetrical stopband rejection predicted by the coupling matrix. We can find a more symmetric solution by making the quad complex (adding a capacitive diagonal coupling). As pointed out by Wenzel,14 however, this simple addition can have a surprising impact on tuning sensitivity.
Finally, we noticed another measured versus modeled result in the literature that supports our analysis. It is another N = 6 folded combline filter. In Zhang et al. (Figure 13),16 the interior rejection peaks predicted by the coupling matrix are symmetric while the measured filter is asymmetric (see Figure 17).
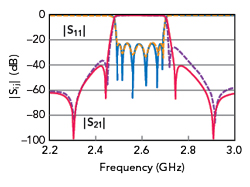
Figure 17 Measured (dashed lines) vs. synthesized (solid lines) responses.16
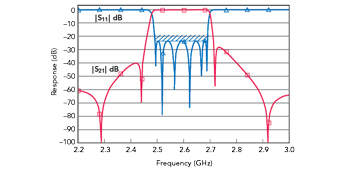
Figure 18 Estimated network theory model for Zhang et al.,12 which agrees with the measurement.
Although no dimensions are given by Zhang et al.,16 we constructed a quick network theory model like Figure 2 based on an estimation of their geometry. With only a simple lumped capacitive coupling from resonator two to five and lumped element resonated couplings at the input and output, we produced the plot in Figure 18, which agrees well with the measured asymmetry.
As in Hagensen,15 the unproved claim is that parasitic couplings are the source of the transmission zero asymmetry. Again, we point out there are no parasitic couplings in the network theory model we derived. Rather, the simple quad is behaving as predicted by Wenzel.14
CONCLUSION
We have demonstrated simulation and design methods for practical combline filters using three distinct combinations of topology and technology. The emphasis is on finding methods that fully predict the filter performance in both the passband and stopbands. We have also pointed out where the popular coupling matrix synthesis may fall short in this regard. Our concern is that a student or novice engineer might assume that any coupling matrix synthesis result fully predicts the performance of the realized combline filter.
In the end, our own filter design flows rely on an early approximation of filter performance with network theory models and then a quick transition to 3D EM models that can be rapidly optimized using port tuning. The port tuning process can be automated to find exact dimensions, when needed, with a minimum number of EM simulations.17 The simple linear interpolation scheme described by Swanson17 is easily understood, far easier to implement and much more efficient than most EM based optimization methods currently available in the literature.
References
- G. L. Matthaei, “Comb-Line Band-Pass Filters of Narrow or Moderate Bandwidth,” Microwave Journal, Vol. 6, No. 8, August 1963, pp. 82–96.
- E. C. Johnson, “New Developments in Designing Bandpass Filters,” Electronic Industries, January 1964, pp. 87–94.
- R. M. Kurzrok, “General Three-Resonator Filters in Waveguide,” IEEE Transactions on Microwave Theory and Techniques, Vol. 14, No. 1, January 1966, pp. 46–47.
- R. M. Kurzrok, “General Four-Resonator Filters at Microwave Frequencies,” IEEE Transactions on Microwave Theory and Techniques, Vol. 14, No. 6, June 1966, pp. 295–296.
- A. E. Atia and A. E. Williams, “Narrow Bandpass Waveguide Filters,” IEEE Transactions on Microwave Theory and Techniques, Vol. 20, No. 4, April 1072, pp. 258–265.
- “Cavity Combline (CCL)” Design Software, DGS Associates, Web: https://www.dgsboulder.com/cavity-combline-ccl.
- R. J. Wenzel, “Synthesis of Combline and Capactively Loaded Interdigital Bandpass Filters of Arbitrary Bandwidth,” IEEE Transactions on Microwave Theory and Techniques, Vol. 19, No. 8, August 1971, pp. 678–686.
- E. G. Cristal, “Tapped-Line Coupled Transmission Lines with Applications to Interdigital and Combline Filters,” IEEE Transactions on Microwave Theory and Techniques, Vol. 23, No. 12, December 1975, pp. 1007–1012.
- I. Shapir, V. A. Sharir and D. G. Swanson, “TEM Modeling of Parasitic Bandwidth Expansion in Combline Filters,” IEEE Transactions on Microwave Theory Techniques, Vol. 47, No. 9, September 1999, pp. 1664–1669.
- “Multiple Coupled Lines in a Rectangular Shield (Dynamic Model) (EM Quasi-Static): RCCOAX Symbol,” Cadence AWR, Web: https://awrcorp.com/download/faq/english/docs/Elements/rccoax.htm.
- D. G. Swanson, “Narrow-Band Microwave Filter Design,” IEEE Microwave Magazine, Vol. 8, No. 5, October 2007, pp. 105–114.
- D. G. Swanson, “A Novel Method for Modeling Coupling Between Several Microstrip Lines in MIC’s and MMIC’s,” IEEE Transactions on Microwave Theory and Techniques, Vol. 39, No. 6, June 1991, pp. 917–923.
- D. G. Swanson and W. J. R. Hoeffer, Microwave Circuit Modeling Using Electromagnetic Field Simulation, Artech House, 2003, pp. 381–383.
- R. J. Wenzel, “Understanding Transmission Zero Movement in Cross-Coupled Filters,” IEEE MTT-S International Microwave Symposium Digest, June 2003, pp. 1459–1462.
- M. Hagensen, “Narrowband Microwave Bandpass Filter Design by Coupling Matrix Synthesis,” Microwave Journal, Vol. 53, No. 4, April 2009, pp. 219–226.
- Y. Zhang, F. Seyfert, S. Amari, M. Olivi and K. Wu, “General Synthesis Method for Dispersively Coupled Resonator Filters with Cascaded Topologies,” IEEE Transactions on Microwave Theory and Techniques, Vol. 69, No. 2, February 2021, pp. 1378–1393.
- D. G. Swanson, “Port Tuning a Microstrip Folded Hairpin Filter,” IEEE Microwave Magazine, Vol. 21, No. 4, April 2020, pp. 18–28.
