Coaxial open-circuit standards are found in many of today’s commercially available vector network analyzer (VNA) calibration kits.1,2 They are most commonly used as standards in calibration schemes such as short-open-load-through (SOLT). In this capacity, they are assumed to have known characteristics, that is, they are assumed to provide a known value of reflection when connected to a VNA test port reference plane. In this respect, it is common practice to consider the open-circuit as a frequency-dependent shunt capacitance, C(f), and to determine the reflection coefficient, Γ, at a given frequency, f, using

where
Y0 = characteristic admittance of the coaxial line (such as 0.02 S)
Y = admittance of the terminating load, G+jB
G = shunt conductance
B = shunt susceptance
For a coaxial capacitor, the loss can be assumed to be zero (G=0) and the susceptance is given by 2πfC. After some manipulation, Equation 1 becomes

where
φ(f) = phase, in degrees, of the reflection coefficient as a function of frequency
This means that if the capacitance of the open-circuit is known, then its reflection coefficient is also known. In particular, at any given frequency, the phase of the reflection coefficient can be determined from the capacitance. In practice, there is often an offset (such as a length of coaxial line) between the connector of the open-circuit and the shunt capacitance. In this article, it will be assumed that a correction has been applied to the phase of the reflection coefficient of the open-circuit to remove the effect of any offset that may be present.
The frequency dependence of the capacitor, C(f), is usually modeled using the following expression, involving a third-order (cubic) polynomial3
![]()
where C0, C1, C2 and C3 are the coefficients of the polynomial.
Most manufacturers of coaxial open-circuits provide generic values for these polynomial coefficients, which are expected to be applicable for all open-circuits of a given type (that is for a given line size and connector type). In practice, however, each manufactured open-circuit will have a unique set of coefficients based on its own construction and constituent parts. Therefore, in order to use a particular open-circuit as a standard to achieve the utmost accuracy, it is important to know (such as through measurements) the coefficients for the individual open-circuit. There is also a quality assurance consideration here, in that quality standards4,5 require that assumed known values of standards are periodically re-assessed to demonstrate whether their known values remain valid or require adjusting, due to extensive use and/or other time-varying effects, for instance.
Based on the above considerations, a research program was undertaken at the UK’s National Physical Laboratory (NPL) to provide a measurement service, traceable to national standards, for determining the capacitance polynomial coefficients for coaxial open-circuits based on precision measurements. This article describes the method adopted and presents some typical results obtained for open-circuits found in commercially available VNA calibration kits.
Obtaining capacitance coefficients from reflection data
The method adopted can be summarized by the following five-step process, as described previously.6
Step 1: Specify the Measurement Model
Measurement, with uncertainty, the reflection coefficient, Γ, of the open-circuit at n frequencies, (f1…fn) using a high precision measurement system.7 The measurement model is given by
![]()
where g describes the functional relationship between input and output quantities and is derived from Equations 2 and 3. Using the n pairs of values of φ(f) and f, the outputs quantities are obtained by solving Equation 4, as a least-squares problem, for C0, C1, C2 and C3.
Step 2: Assign a Distribution to the Input Quantities
The next step is to assign a distribution to the input quantities, that is the n values of the phase of the reflection coefficient, φ(f). Therefore, an n-dimensional normal distribution with mean vector
![]()
and a diagonal co-variance (or uncertainty) matrix

are assigned to the measured phase values. It is assumed that the phase values measured at different frequencies are uncorrelated and so all off-diagonal elements in the uncertainty matrix are zero. It is further assumed that the uncertainty in frequency is negligible.
Step 3: Generate a Large Random Sample from the Distribution of Input Quantities
A large random sample of size m (where m is typically 50,000) is generated from the n-dimensional normal distribution assigned to the measured phase values, above. (This is an implementation of the Monte Carlo method, which involves performing statistical sampling experiments using a computer.) For example, this can be achieved using the procedure described in Reference 8. The sample is represented by the following (m×n) matrix in which each row represents an n-dimensional point corresponding to the phase measured at the n frequencies, f1…fn.

Step 4: Apply the Measurement Model to Obtain a Corresponding Large Sample from the Distribution of the Output Quantities
Applying the measurement model to each row in Equation 5 gives m sets of capacitance coefficients (C0, C1, C2, C3), which can be represented by the following matrix

Step 5: Obtain Estimates for the Measurands
The required information—mean value and uncertainty information—for each capacitance coefficient is extracted from the columns in Equation 6. Since this process determines four polynomial coefficients simultaneously, the associated uncertainty information is represented by a (4×4) uncertainty matrix. The diagonal elements of this matrix represent the squares of the standard uncertainties (that is variances) in each polynomial coefficient and the off-diagonal elements represent the co-variances of these polynomial coefficients.

An expanded uncertainty (at a specified level of confidence) for each capacitance coefficient can be obtained by arranging the data in each column of Equation 6 in order of size and establishing an interval that encompasses the desired proportion of values (such as 95 percent). The co-variances can be used to determine the amount of correlation (in terms of correlation coefficients) between the capacitance polynomial coefficients. A correlation coefficient describes the degree to which variations in two components are interrelated. For example, if a variation in some physical process (such as connector misalignment) causes both components to increase, then these components are said to be positively correlated (indicated by a correlation coefficient with a positive value). If, on the other hand, a variation in the physical process causes one component to increase while the other component decreases, then this is termed negative correlation (indicated by a correlation coefficient with a negative value). Values of correlation coefficient can range from –1 to +1. This information, along with the mean measured values for each polynomial coefficient, is included on the certificate of calibration that is issued by the NPL measurement service for the open-circuit.
Example 1: Precision 7 mm Open-circuit

To illustrate the above technique, the reflection coefficient of a precision 7 mm open-circuit (from an Agilent 85050C VNA calibration kit)1 was measured from 1 to 18 GHz using an NPL’s primary standard VNA measurement system,7 which provides an assessment of the overall uncertainty of the measurements. The resulting capacitance coefficients are shown in Table 1. The achieved uncertainty of measurement is dependent on the number of measured values used to determine the capacitance coefficients (that is the number of frequencies at which reflection measurements were made). In general, the more values used, the more accurate the determinations. Here, 35 values were generated from reflection measurements made every 0.5 GHz.
An additional benefit in using this method is that it is possible to view the distribution of values for each determined capacitance coefficient. The overall shape of the distribution can quickly reveal any unusual behavior that may be present in a given measurement quantity (such as if the distribution is skewed or departs significantly from the characteristic ‘bell’ shape of the usually assumed normal distribution). For example, Figure 1 shows the distributions, presented as histograms, obtained during the determination of the capacitance coefficients in Table 1. Strictly speaking, these are marginal (uni-variate) distributions of the underlying four-dimensional (multi-variate) distribution for C0, C1, C2 and C3. It is clear that these distributions look reasonably ‘normal’ and therefore one would not expect any unusual behavior in the presented results.

For completeness, Table 2 shows the correlation coefficients between the four capacitance terms determined during the measurements. This table shows that pairs of capacitance coefficients are either strongly positively correlated (that is correlation coefficient close to +1) or strongly negatively correlated (correlation coefficient close to –1). For example, there is strong positive correlation between the determinations of C0 and C2 and between the determinations of C1 and C3. There is strong negative correlation between the remaining pairs of capacitance coefficients. In principle, this correlation information should be taken into account, depending on where the values of these capacitance coefficients are used (when propagating uncertainties to other measurement quantities, for example).9 This is why this information is included on the certificate of calibration for each measured open-circuit.
Deriving Phase Values from Capacitance Coefficient Values
Table 1 also shows the manufacturer’s specified generic values for this type of open-circuit. These are often stored on the calibration coefficients disk supplied with the calibration kit containing the open-circuit standard. It can be seen from this table that all the manufacturer’s values for these coefficients fall inside the 95 percent confidence intervals for the corresponding measured values, that is the two sets of capacitance coefficients appear to show good agreement. Equations 2 and 3 can be used to generate phase values in a range of frequencies, using either the measured or the manufacturer’s capacitance coefficients. In the case of the measured values, this can be done for each set of capacitance coefficients in Equation 6, that is for each row of Equation 6, generating a vector of m phase values
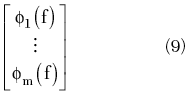
This vector contains information about the distribution of φ(f) and can therefore be used to establish a 95 percent prediction interval for φ(f). For example, this can be achieved by sorting the components of Equation 7 into ascending order and then obtaining the 0.025 and 0.975 percentiles. Extra care is needed if the components of Equation 7 fall on either side of the “cut” in the phase scale at ±180°. This prediction interval takes into account the uncertainties in the measured capacitance coefficients and also any correlation between them.
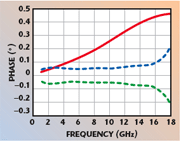
Figure 2 shows the 95 percent prediction interval (dashed curves) for the phase predicted from the measured capacitance coefficients, normalized so that the predicted phase is set to zero. The phase predicted using the manufacturer’s capacitance coefficients (solid curve), similarly normalized, is also shown. The two predictions clearly disagree since the manufacturer’s prediction curve lies outside the 95 percent prediction interval derived from the measured capacitance coefficients over most of the frequency range. Thus, although the measured capacitance coefficients appear to show good agreement with the manufacturer’s capacitance coefficients, the phase curves derived from the two sets of coefficients clearly disagree. In other words, a small change in the capacitance coefficient (such as that between the measured and manufacturer’s values) can result in a relatively large change in the predicted phase curve. Presumably, this is a result of the strong correlation between the capacitance coefficients. For this reason, when making use of the capacitance coefficients, care needs to be taken to retain a sufficient number of significant figures in order to not unduly affect the predicted phase curve. The maximum difference between the two-phase predictions approaches 0.5° at 18 GHz. Since the wavelength at 18 GHz is approximately 17 mm, this phase error equates to an equivalent ‘length’ error of approximately 25 μm. Under normal circumstances, for measurements in precision coaxial lines at these frequencies, one would expect the S-parameter measurement accuracy of a VNA, when expressed in these ‘length’ terms, to be of the order of only a few microns (that is a VNA should make a reasonably good ‘electrical micrometer’). Therefore, in light of the above, an error of 25 μm is excessive and unnecessarily detrimental to the overall achievable accuracy for a VNA.
To investigate this error further, a phase error, u(φ), can be converted to an equivalent error in linear magnitude, u( | Γ |), using the following formula10

This assumes that the error in the reflection coefficient is represented by a circle of radius u( | Γ | ) in the complex plane. This is a simplified representation of a more general view that has been discussed previously.11 However, applying this simplified representation is sufficient to illustrate the point.
With u(f) = 0.5° at 18 GHz and choosing | Γ | = 1, this gives
![]()
This error in reflection coefficient magnitude is large, compared with other similar published values for the achieved accuracy of VNAs.12

Figure 3 shows the impact of this uncertainty in the open-circuit standard, on subsequent reflection measurement, by plotting an uncertainty profile13 for a short-open-load (SOL) calibration scheme with the uncertainty in the open-circuit standard taken to be u(|Γ|) = 0.01. Here, the uncertainties of the matched load and short-circuit standards are taken to be zero. Of course, in practice, the uncertainties in the matched load and short-circuit will also be non-zero. This surface indicates the uncertainty that may be present in an SOL calibration scheme if one relies only on the manufacturer’s specified capacitance coefficients. By using the measured capacitance coefficients instead of the manufacturer’s values, these uncertainties should be substantially reduced. From Figure 2, the maximum phased prediction error, based on the measured capacitance coefficients, is approximately 0.2° at 18 GHz. This equates to a worst-case error of approximately u(|Γ|) = 0.003.
Example 2: LA Techniques Precision 2.92 mm Open-circuit

As a second example, an open-circuit manufactured by LA Techniques2 for use in the frequency range 3 MHz to 3 GHz was measured. This (male) open-circuit is effectively a coaxial end cap that attaches to a female precision 2.92 mm connector (used to form the VNA’s test port). The values obtained for the capacitance coefficients, using the method previously described, are listed in Table 3, together with the expanded uncertainties (at a level of confidence of 95%). As before, the achieved uncertainty of measurement is dependent on the number of measured values used to determine the capacitance coefficients. Here, 99 values were generated from reflection measurements made approximately every 30 MHz to 3 GHz, this being the maximum operating frequency of the LA Techniques VNA that uses this open-circuit during calibration. It should be noted that these capacitance coefficient values are only considered to be applicable within the bandwidth of the reflection coefficient measurements used to obtain them. Here, the frequencies of the reflection coefficient measurements were chosen to approximate the bandwidth of use for the open-circuit (3 MHz to 3 GHz). However, if the open-circuit is used at frequencies outside this bandwidth, then these capacitance coefficients should be re-evaluated using reflection coefficient measurements obtained at frequencies chosen to represent the modified bandwidth.
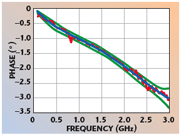
For the results shown, it was again found that the (marginal) distributions associated with the capacitance coefficients were fairly ‘normal’ and that pairs of capacitance coefficients are strongly correlated (either positively or negatively). Figure 4 shows the phase of the reflection coefficient (red) as measured by the NPL’s primary standard VNA measurement system,7 the phase predicted from the extracted capacitance coefficients (blue) and the 95 percent prediction interval for phase (green), based on the capacitance coefficients. The manufacturer (LA Techniques) is planning to use the capacitance coefficient values of Table 3 as generic values for this design of open-circuit when used in the frequency range 3 MHz to 3 GHz.
Conclusion
A method has been presented for obtaining traceable values for the capacitance coefficients of coaxial open-circuits, derived from reflection coefficient measurements. Some sample results for a precision 7 mm open-circuit have been given. It has been shown that even when the values for the capacitance coefficients agree with those supplied by the manufacturer within the measurement uncertainties, relatively large errors in the predicted reflection coefficient for the open-circuit can still result due to the strong correlation between the capacitance coefficients. This can lead to a substantial component of uncertainty for subsequent VNA measurements when the open-circuit, used as a standard, has not been individually characterized (such as by using the method described in this article). Results have also been given for a male open-circuit in the 2.92 mm line size, which the manufacturer will use as generic values for all open-circuits of this design for the frequency range 3 MHz to 3 GHz. Where possible, the actual capacitance for a given open-circuit should be established through traceable measurements, and the capacitance coefficients so determined should be used for specifying the open-circuit during a VNA calibration process.
Acknowledgment
The authors would like to thank Nils Nazoa of LA Techniques for loaning the 2.92 mm open-circuit standard. The work described in this article was funded by the UK Government and, specifically, by the Electromagnetic and Measurement for Innovators Programs of the National Measurement System Directorate, Department of Trade and Industry. ©Crown Copyright 2006. Reproduced by permission of the Controller of HMSO.
References
1. Agilent Technologies 85050C 7 mm Precision Calibration Kit – User’s and Service Guide, Agilent Part Number 85050-90051, June 2002.
2. LA Techniques 2.92 mm Connector Calibration Kits, http://www.latechniques.com/.
3. Network Analysis: Specifying Calibration Standards for the HP 8510 Network Analyzer, HP Product Note 8510-5A, February 1988.
4. Measurement Management Systems—Requirements for Measurement Processes and Measuring Equipment, ISO/IEC 10012: 2003, International Organization for Standardization, Geneva, Switzerland.
5. General Requirements for the Competence of Testing and Calibration Laboratories, ISO/IEC 17025:2005, International Organization for Standardization, Geneva, Switzerland.
6. N.M. Ridler and M.J. Salter, “A Generalized Approach to the Propagation of Uncertainty in Complex S-parameter Measurements,” 64th ARFTG Conference Digest, December 2–3, 2004, Orlando, FL, pp. 1–14.
7. N.M. Ridler, “A Review of Existing National Measurement Standards for RF and Microwave Impedance Parameters in the UK,” IEE Colloquium Digest, No. 99/008, February 1999, pp. 6/1–6/6.

Martin J. Salter
8. M.J. Salter, N.M. Ridler and M.G. Cox, “Distribution of Correlation Coefficient for Samples Taken from a Bi-variate Normal Distribution,” NPL Report CETM 22, September 2000.
9. N.M. Ridler and M.J. Salter, “Propagating S-parameter Uncertainties to Other Measurement Quantities,” 58th ARFTG Conference Digest, San Diego, CA, November 29–30, 2001.
10. J.P. Ide, “NPL’s Expression of Uncertainty for Scattering Coefficient Measurements,” ANAlyse Technical Note, No. 17, May 1996 (available from www.npl.co.uk/anamet).
11. N.M. Ridler and M.J. Salter, “Evaluating and Expressing Uncertainty in Complex S-parameter Measurements,” 56th ARFTG Conference Digest, Boulder, CO, November 30 and December 1, 2000, pp. 63–75.
12. N.M. Ridler and C. Graham, “Some Typical Values for the Residual Error Terms of a Calibrated Vector Automatic Network Analyzer (ANA),” BEMC 99 – 9th International Conference on Electromagnetic Measurement, Brighton Metropole Hotel, UK, November 2–4, 1999, pp. 45/1–45/4.

Nick M. Ridler
13. P.R. Young, “Propagation of Uncertainty in One-port ANA Measurements,” ANAMET Report 017, August 1998 (available from www.npl.co.uk/anamet).
Martin J. Salter received his BSc degree from the University of Manchester, UK, and his MSc degree from the University of London, UK, in 1986 and 1992, respectively. Since 1986, he has been with the UK’s National Physical Laboratory (NPL), where is has been involved with UHF and VHF antenna measurements and more recently with the development of RF and microwave impedance standards and with the treatment of measurement uncertainty for vector-valued quantities.
Nick M. Ridler received his BSc degree from the University of London, UK, in 1981. He has since spent almost 25 years working in both industrial and government scientific research laboratories. He is currently lead scientist and principal research scientist at the UK’s National Physical Laboratory (NPL). His current research interests include millimeter-wave, on-wafer measurements, uncertainties for vector measurements and providing instrument traceability remotely using the Internet.
