Traditional style isolators sold commercially over the past 50 years are highly susceptible to low level stray magnetic fields. Even in relatively weak stray fields, insertion loss can exceed 30 dB rendering the device unusable. In contrast, newer magnetically saturated type isolators function remarkably well in stray fields.
Faraday rotation isolators employ magnetically biased ferrite rods to rotate the polarization of an RF signal and are thus susceptible to stray magnetic fields. Stray magnetic fields are defined as those arising from sources external to the isolator and are not magnetic fields generated by the internal magnets used to bias the ferrite. The offending stray fields can arise from other nearby ferrite components but are also common in a variety of mmWave experiments like dynamic nuclear polarization,1 particle accelerators2 and tokamak fusion reactors.3 Stray magnetic fields can, in principle, alter the magnetic bias point in the ferrite and cause under- or over-rotation of the RF signal resulting in increased insertion loss and decreased isolation. Test results described demonstrate that traditional style isolators sold commercially over the past 50 years are highly susceptible to low level stray magnetic fields. Even in relatively weak stray fields, insertion loss can exceed 30 dB rendering the device unusable. In contrast, newer magnetically saturated type isolators function remarkably well in stray fields up to and exceeding 250 Oe.
ISOLATOR OPERATION
Isolators are non-reciprocal devices, passing EM signals in one direction and absorbing them in the reverse direction. They are primarily used to suppress standing waves that arise from signal reflections caused by impedance mismatches between highly tuned components in microwave and mmWave systems. Standing waves limit system bandwidth and cause dips or even nulls in the final output. Standing waves can be mitigated by inserting isolators between mismatched components resulting in a smoother frequency response and improved bandwidth.
The isolator topology most frequently used at mmWave frequencies is the Faraday rotation type first described by Barnes in 1961.4 This isolator employs a ceramic cone to couple a TE10 rectangular waveguide mode to a TE11 mode in a cylindrical ferrite rod. The signal polarization is rotated by 45 degrees as it passes through the ferrite rod and is then coupled to an output waveguide via a second ceramic cone.
Figure 1 shows the layout of the waveguides, ceramic cones and ferrite rod in a typical isolator. The black arrows at the center of the input and output waveguides indicate the polarization of the primary TE10 waveguide mode. The input and output waveguides are canted at 45 degrees with respect to each other. The ferrite rod spans the gap between the waveguides and has a diameter roughly equal to the waveguide height. Each cone has a resistive layer that bisects the central axis. The resistive layers are oriented such that they are normal to the TE10 mode polarization in their respective waveguides.
Figure 2 shows the electric field polarization vector orientations of the forward and reverse traveling signals. Both signals rotate in the same direction (CCW for the purpose of this illustration). The forward traveling signal is normal to the resistive layers in both cones, minimizing loss and signal attenuation. The polarization vector of the reverse traveling signal is aligned with the resistive layer in the input waveguide causing the signal to be absorbed.

Figure 1 Sketch showing the waveguides, ceramic cones and ferrite rod in a Faraday rotation isolator.

Figure 2 Rotation of the forward and reverse traveling signals as they pass through the ferrite rod.
The rotation angle, θ, of the signal as it passes through the ferrite rod is directly proportional to the ferrite magnetization, 4πMZ, and the ferrite length, l, as shown in Equation (1).
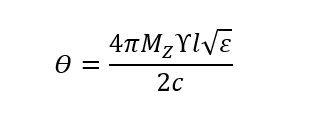
where, 4πMZ is the axial magnetization
ϒ is the gyromagnetic ratio,5

l is the ferrite length
c is the speed of light
ε is the ferrite dielectric constant
An external magnetic field is used to align magnetic dipoles in the ferrite giving rise to the desired axial magnetization, 4πMZ. Rare earth magnets are often used, typically neodymium (Nd2Fe14B) or samarium cobalt (SmCo5 or Sm2Co17). As the magnetic bias field increases, additional dipoles are aligned and the magnetization, 4πMZ, increases until reaching a point of saturation denoted as the saturation magnetization, 4πMS, beyond which further increases in the applied magnetic field have little effect. The magnitude of the saturation magnetization is a material dependent property and varies in the range 300-5000 gauss for most commercial ferrites. Ferrite material with 4πMS = 5,000 gauss5 is typically used in mmWave isolators. The saturation magnetization is temperature dependent, following a modified Bloch law and reaching a maximum value at absolute zero (0 K) since it is easier to align magnetic dipoles at lower kinetic energy levels.
The dipoles precess around the magnetic bias field vector as shown in Figure 3. As an EM signal passes through the ferrite, the fields interact with the dipole moments. Linearly polarized waves, like those passing through the isolator, can be decomposed into left-hand circularly polarized (LHCP) and right-hand circularly polarized (RHCP) waves. The interaction with the precessing dipole moments yields disparate propagation constants for the RHCP and LHCP waves. The difference in the propagation constants arises because one of the components (RHCP or LHCP) opposes the dipole precession and the other coincides with it. As a result, a phase shift occurs between the RHCP and LHCP waves as they propagate through the ferrite. This gives rise to the rotation of the linearly polarized signal. More in-depth discussions on Faraday rotation are given by Pozar,6 Lax et al.7 and Balanis.8

Figure 3 Angular momentum and spin magnetic dipole moment vectors.
Faraday rotation isolators can be classified into two basic categories: 1) magnetically saturated and 2) non-saturated (see Figure 4). They can usually, but not always, be identified by size and shape. A saturated isolator is smaller and does not have a magnetic sheath. The traditional non-saturated isolator is typically much larger and most have hollow cylindrical magnetic sheaths around their center sections.

Figure 4 Saturated (a) and traditional non-saturated (b) WR-10 Faraday rotation isolators.
Figure 5 shows a traditional non-saturated Faraday rotation isolator with the magnetic sheath and waveguides removed. The magnetic bias field is adjusted by rotating the magnet off axis until maximum isolation is achieved and then locking down the magnet with an epoxy. The long ferrite rod used in the non-saturating isolators is lossy at mmWave frequencies leading to high insertion loss, but the ability to fine tune the rotation while testing in-situ is a powerful tool.

Figure 5 Canted magnet in a traditional isolator.
A saturated isolator use a much shorter ferrite rod and a saturating magnetic bias field to achieve the required 45 degrees of rotation. It is thus much smaller than the traditional isolator and has much lower insertion loss.
STRAY MAGNETIC FIELD TESTS
Laboratory tests are conducted in W-Band (75-110 GHz) to determine the effects of stray magnetic fields. Two isolators are tested, one made by Micro Harmonics (saturated type) and a traditional style isolator made by another vendor (unsaturated type). Since traditional style isolators have similar construction regardless of the manufacturer, the tested traditional style isolator is thought to be representative of its entire class. The tests are conducted using a Keysight N5222B PNA (vector network analyzer) and a pair of VDI W-Band frequency extenders. The isolators are subjected to both normal and axial stray magnetic fields. Normal stray fields are oriented at a 90 angle angle to the magnetic bias field and axial stray fields are parallel to the bias field. The test apparatus used to produce normal stray magnetic fields is shown in Figure 6. The maximum field produced by the apparatus is measured to be ± 65 Oe.

Figure 6 Saturated isolator in the normal stray field test fixture (a), sketch of normal stray field test apparatus showing the direction of the magnetic field (b) and a traditional style non-saturated isolator in the normal stray field test fixture (c).
A magnetic coil is used to produce the axial stray magnetic fields as shown in Figure 7. The coil has 787 turns of 24 AWG magnet wire, an inner diameter of 38 mm and a length of 25 mm. The maximum axial field is measured at more than ± 260 Oe at the coil center. Both normal and axial stray fields are calibrated using Hall effect sensors; however, magnetic materials used in the isolators may perturb the stray field intensity at the ferrite location when the isolators are inserted into the test apparatus.

Figure 7 Traditional style isolator in the axial stray field test fixture (a), saturated isolator in the axial stray field test fixture (b) and the Hall probe calibration of the axial magnetic field coil (c).
