Normal (Orthogonal) Stray Magnetic Field Tests
Full two port S-parameter data is recorded from 75 to 110 GHz as the calibrated normal stray magnetic field is varied. For simplicity, only data at the band center (92.5 GHz) is shown. Insertion loss (IL) and isolation (Iso) for the two isolators is shown in Figure 8 for a normal stray magnetic field ranging from 0 to 65 Oe. Insertion loss of the saturated isolator remains nearly constant at 0.5 dB, while insertion loss of the traditional isolator remains constant at 1.7 dB. There is no change in isolation of the saturated isolator, which remains constant at 28 dB. Isolation of the traditional style unsaturated isolator, however, drops from 39 to 29 dB, a relatively minor effect.
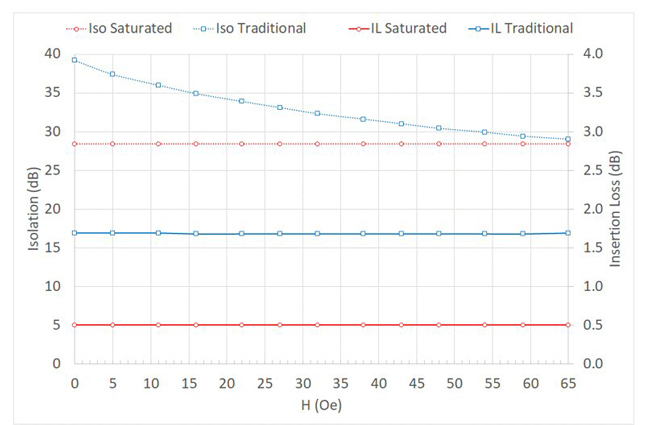
Figure 8 Test data for a saturated (red) and traditional style unsaturated isolator (blue) under a normal (orthogonal) stray magnetic field. The test data is taken at a W-Band center frequency of 92.5 GHz.
Both isolators perform well under exposure to orthogonal stray magnetic fields. The magnetic sheath used in the traditional isolator efficiently diverts the normal stray magnetic field around the isolator body and away from the ferrite. The strong magnetic bias field used in the saturated isolator keeps the magnetic dipoles aligned in the presence of the normal stray magnetic field.
Axial Stray Magnetic Field Tests
Test results are summarized in Figure 9. Insertion loss and isolation of the saturated isolator are shown in the red curves. Insertion loss remains constant at 0.5 dB when subjected to stray axial magnetic fields between 220 Oe and +220 Oe. Isolation drops from 32 dB at – 220 Oe to 25 dB at +220 Oe, indicating that the ferrite rod is slightly too long for peak performance.
Insertion loss and isolation of the traditional isolator are shown in the blue curves. In this case, they vary widely as a function of axial stray magnetic field. With no stray field (H=0), the isolation is 30 dB and insertion loss is 1.7 dB. When the stray axial field is increased by ± 38 Oe, however, both insertion loss and isolation are 4.7 dB; the traditional style isolator degenerates to a bi-directional attenuator. At a magnetic field strength of 80 Oe, isolation and insertion loss values are reversed. The traditional style isolator, once again, behaves as an isolator, but in the reverse direction. The magnetic sheath is clearly ineffective against axial stray magnetic fields. This is not surprising since the sheath has the form of a hollow cylinder with an inner diameter near 25 mm, far from the ferrite rod.

Figure 9 Test data for a saturated (red) and traditional style (blue) isolator under exposure to an axial stray magnetic field. Test data is at taken 92.5 GHz
ANALYSIS
The extrema in the data and the points where isolation and insertion loss curves cross correspond to changes in the signal rotation of N*45 degrees, where N is an integer having the range – 5 to +3 and inclusive of 0. Figure 10 shows the cross-section of the transition region between the ferrite rod and the rectangular waveguides. The ferrite is indicated by a shaded circle and the orientation of the resistive layer is shown as a dashed line. Since dipole precession is fixed by the magnetic bias field, both the forward and reverse traveling signals rotate in the CCW direction as they pass through the ferrite rod. This is the basis for the non-reciprocal behavior of the Faraday rotation isolator. In the absence of a stray magnetic field, the signals rotate 45 degrees CCW as they make a single pass through the ferrite. The forward traveling signal impinges on the output waveguide with the polarization aligned to the TE10 mode and is coupled to the output waveguide. The reverse traveling signal impinges on the input waveguide with the polarization aligned to the resistive layer in the input cone and is absorbed. This is the normal operating condition.
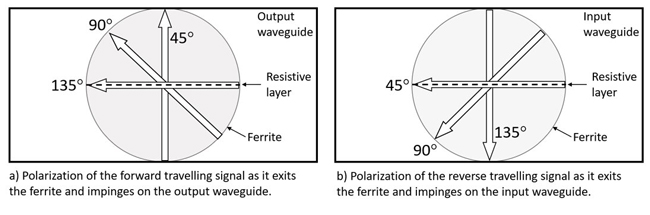
Figure 10 Polarizations of forward (a) and reverse (b) signals after a single pass through the ferrite rod.
If an axial stray magnetic field is applied with sufficient magnitude to double the ferrite magnetization, both the forward and reverse traveling signals undergo an additional 45 degrees of rotation (90 degrees total). The respective signal polarizations are indicated as 90 degrees in Figure 10. Both the forward and reverse traveling signals now have equal vector components aligned to the resistive layer and the TE10 mode. Half of the signal power (3 dB) is absorbed in the resistive layer and half couples to the TE10 mode. Since the 3 dB split occurs at both the input and output waveguides at exactly the same magnetic bias condition, insertion loss and isolation have the same value (|S21| = |S12|). The actual measured values are 4.7 dB rather than 3 dB due to an additional 1.7 dB loss in the ferrite rod.
If the stray magnetic field is further increased so that the rotation increases another 45 degrees (135 degrees total), the reverse traveling signal polarization is aligned to the TE10 mode in the input waveguide and the forward traveling signal is aligned to the resistive layer located in the cone in the output waveguide. The signal polarizations are shown labeled as 135 degrees in Figure 10. The isolator now works in the reverse direction, absorbing forward traveling signals and passing reverse traveling signals. Reversing the polarity of the axial stray magnetic field causes the same series of events to occur with the signal rotation now in the clockwise direction.
The measured data in Figure 9 gives the value of the magnetic field, H, for the extrema and the crossings. As described, these are the points at which the rotation is an integer value of 45 degrees. The ferrite rods used in traditional style isolators are typically 6 mm long as reported by Erickson.9 Using the equation for rotation, Equation (1), with θ = 45 degrees and l = 6 mm, yields a magnetization of 4πMZ = 1,258 gauss. Each 45 degree rotation step therefore corresponds to a magnetization increment of 1,258 gauss.
The resulting plots of magnetization, 4πMZ, versus magnetic field, H, are shown in Figure 11. Two curves are shown because of a small hysteresis observed in the data. The red curve is obtained by starting at the highest possible negative field (about – 260 Oe) and reducing the magnitude. The red data points are thus taken in order from left to right on the graph. The blue data points are taken in order from right to left on the graph. The blue and red data points represent the crossings and peaks in the measured data. The dashed lines are fourth order polynomial curve fits to the data.
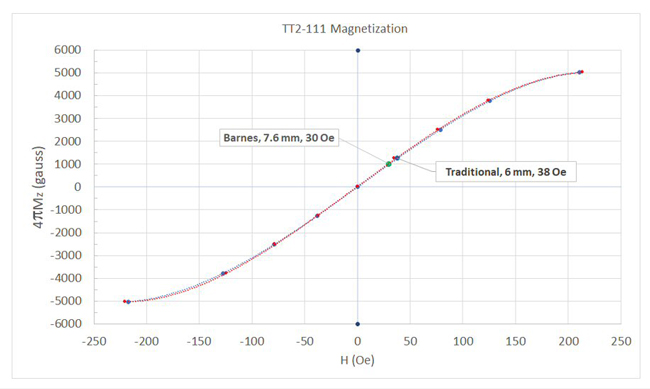
Figure 11 Measured magnetization curves for ferrite with 4πMS = 5,000 gauss.5
The plotted curves in Figure 11 reach saturation near 5,000 gauss. Negative values of 4πMZ are used to denote reversal of the magnetic field polarization. Additional interim data points may be obtained by constructing an isolator with a longer ferrite rod. The magnetic bias point of the traditional style isolator is indicated on the graph. The magnetic bias field used in the Micro Harmonics isolators has been measured at more than 700 Oe and therefore does not fit on the graph. At 700 Oe the bias point is hard into saturation where the slope of the magnetization curve, dMZ/dH, is near zero, which explains the saturated isolator’s insensitivity to stray magnetic fields.
Barnes4 reported using a 7.6 mm length of ferrite rod with 4πMS = 5,000 gauss and a magnetic field near 30 Oe. Using Equation (1), the calculated magnetization required to rotate the signal by 45 degrees is 990 gauss. This data point also falls on the measured magnetization curves in Figure 11.
CONCLUSION
Traditional style Faraday rotation isolators employing a magnetic sheath are highly sensitive to stray magnetic fields. The magnetic sheath gives good protection against stray magnetic fields that are orthogonal to the magnetic bias field but provides little or no protection against axial stray magnetic fields aligned parallel to the bias field. This is expected since the magnetic sheath has the form of a hollow cylinder with an inner diameter near 25 mm, far from the ferrite rod. Figure 11 shows that the magnetic bias point of the traditional isolator is on the steep part of the magnetization curve where small changes in the magnetic bias field, H, give rise to relatively large changes in the magnetization, 4πMZ. This in turn causes large changes in the signal rotation and results in severely degraded isolator performance. The long ferrite used in traditional style unsaturated isolators also causes high insertion loss at higher millimeter-wave frequencies. The insertion loss of the traditional isolator was measured to be 1.7 dB at 92.5 GHz.
In contrast, magnetically saturated isolators are highly resistant to the effects of stray magnetic fields, both axial and orthogonal, even though the isolators do not employ magnetic sheaths. Resistance to stray magnetic fields arises from the fact that the ferrite is biased hard into saturation where the slope of the magnetization curve is near zero. Relatively large changes in the magnetic bias caused by stray magnetic fields have little effect on the magnetization. Saturated isolators also employ much shorter ferrite rods, which significantly reduces insertion loss. Insertion loss of the Micro Harmonics isolator is 0.5 dB at 92.5 GHz.
ACKNOWLEDGMENTS
We would like to thank NASA JPL for their continued support of this work through research contracts NNX15CP37P, NNX16CP07C, 80NSSC18P2018 and 80NSSC19C0148.
References
- Q. Z. Ni, E. Daviso, T. V. Can, E. Markhasin, S. K. Jawla, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, “High Frequency Dynamic Nuclear Polarization,” Accounts of Chemical Research, Vol. 46, No. 9, April 2013, pp. 1933–1941.
- M. C. Downer, R. Zgadzaj, A. Debus, U. Schramm and M. C. Kaluza, “Diagnostics for Plasma-Based Electron Accelerators,” Reviews of Modern Physics, Vol. 90, August 2018.
- H. -J. Hartfuß and T. Geist, Fusion Plasma Diagnostics with mm-Waves: An Introduction, Wiley‐VCH Verlag GmbH & Co, 2013.
- C.E. Barnes, “Broad-Band Isolators and Variable Attenuators for Millimeter Wavelengths,” IRE Transactions on Microwave Theory and Techniques, Vol. 9, No. 6, November 1961, pp. 519-523.
- “Products for RF/Microwave Applications,” Ferrite TT2-111, Trans-Tech Corporation. Web. https://datasheet.octopart.com/SR9000SPQ0472AY-Trans-Tech-datasheet-8861441.pdf.
- D. Pozar, Microwave Engineering, 4th Edition, John Wiley & Sons, 2012.
- B. Lax and K. Button, Microwave Ferrites and Ferrimagnetics, McGraw-Hill, New York, 1962.
- Constantine A. Balanis, Advanced Engineering Electromagnetics, Wiley; 2nd edition, 2012.
- N. R. Erickson, “Very Low Loss Wideband Isolators for mm-Wavelengths,” IEEE International Microwave Symposium Digest, May 2001, pp. 1175-1178.
