
Figure 1 VNA-based setup for measuring the IMD of a mm-wave circuit.
Higher power millimeter wave (mm-wave) devices and more demanding applications are increasing the need for accurate mm-wave intermodulation distortion (IMD) measurements. While a variety of expressions are still needed, as at microwave frequencies – intercept points, relative product levels, intermodulation distortion (IMD) product asymmetry – the challenges can be intensified in terms of absolute power accuracy, measurement receiver linearity effects, combiner behavior and other areas. Typical measurement behaviors in these categories will be explored in a vector network analyzer (VNA) context, along with some approaches that can help to optimize accuracy.
While IMD measurements have been very popular at RF and microwave frequencies for decades, the progress in mm-wave technologies of late has enabled higher power devices in the higher frequency ranges, making those same measurements also of interest in the mm-wave domain. Whether it is GaN-enabled, watt-class power amplifiers at W-Band or combined structures enabling high linearity at E-Band or higher, the IMD measurement is a potentially important part of the qualification and specification process. The basic concept of two tones generating in-band (and out-of-band) mixing products in the device is no different, but some of the measurement challenges can be heightened. While the basics can be found elsewhere,1,2,3 this article will focus on some of the measurement details for this higher frequency class of devices.
It is useful to reintroduce some of the common IMD metrics that are used in all frequency ranges as well as abbreviations used in this article. Here they are all generalized to nth order products, although third order is the most common, meaning where the products land one tone delta away on either side of the main tones (delta refers to the spacing between the two stimulus tones):
- IPn – nth order intercept point
- IMn – nth order intermodulation product relative to either one or an average of the main tones
- PWRn – Absolute power of the nth order intermodulation product
- ASYMn – nth order product asymmetry, i.e., the difference between the upper and lower product levels

Figure 2 The effect of the calibration frequency list on the residual accuracy of a receiver calibration.
The intercept point is an often quoted metric, although it does have its weaknesses. It is an ideal projection of the power level (input or output referred) where the main tone power and the product power would be equal based on one measurement. The issue with this approach is that the calculated projection is normally a strong function of power, so the result based on a measurement at a single power may be an anomaly rather than typical. Asymmetry, the imbalance of the products, is becoming an increasingly important metric, as it can reveal memory effects that might be generated by thermal or bias system time constants, which can affect modulated distortion, particularly relatively close to the carrier.4
A VNA-based measurement setup using mm-wave modules (usually broadband, but they can be narrower band) is shown in Figure 1. While many different configurations are possible, often the highest frequency signals are generated and down-converted (on the receive side) in modules close to the device under test (DUT), to minimize cable loss. Other instruments could certainly be used, but the integrated calibration capabilities (in terms of signal power and receiver calibration at any reference plane) and ability to perform other measurements on the DUT can make a VNA platform attractive.
MEASUREMENT CHALLENGES
In terms of measuring IMD quantities at mm-wave frequencies, a number of aspects become more challenging.
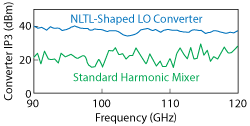
Figure 3 The structure and LO drive behavior of the receiver can have a significant impact on the net receiver linearity, setting the maximum IPn that can be measured.
Power Accuracy: If one is concerned with a relative metric like IMn, one may think absolute power accuracy is less important, but the operating point of the DUT is often a critical part of the measurement setup. The DUT IM level will usually change by multiple dB for a 1 dB change in drive power. Power calibration and measurement are somewhat more challenging at mm-wave frequencies, as basic power meter accuracy can degrade and often the return loss in the test setup (and the DUT) is not as high. As return loss is a dominant power measurement accuracy term, this can be quite important. In a common W-Band power measurement configuration, sensor linearity may limit accuracy to 2 percent, basic power sensor calibration factor uncertainty may be 3 percent, but mismatch (with a 14 dB return loss port) may contribute 4 percent. The net uncertainty can be on the order of 0.5 dB in many cases.
Short of a higher level of traceable power sensor calibration, perhaps the one way to improve these uncertainties is to optimize match in the test setup. Correction for mismatch at the DUT ports can be helpful, particularly for absolute measurements, but this does not address the operating point concern. In all cases, the DUT return loss can be a larger issue for larger deltas, as the product and main tones may see different mismatch levels.
Receiver Calibration: On the stimulus side, a local power calibration can take care of test setup losses on the input but output-side network losses can be quite important at higher frequencies, particularly for the absolute metrics (and for relative metrics if the delta is large). A power-referred receiver calibration at the DUT output reference plane helps to minimize these issues and, if delta is large, is aided by a sufficiently dense frequency list. The latter can come about since the network losses may vary significantly over the scale of tens or hundreds of MHz, depending on the structure. As an example, Figure 2 shows the net receiver calibration error when a full frequency list is used (the “dense” trace) compared to a calibration at only the main tone frequencies (the “sparse” trace). The test system was designed for E-Band but included some substantial cable runs to allow other measurements. The resulting error is mainly connector/cable repeatability; at non-calibrated frequencies, it could exceed 0.5 dB with a reasonably well-matched setup (i.e., 15 dB return loss). Using the dense frequency list and calibrating at product as well as main tone frequencies helps significantly.

Figure 4 A simplified diagram of the signal generation for IM, including the leveling circuitry.
Receiver Linearity: In terms of the measurement, receiver linearity can be a limiting factor for more linear DUTs. Many mm-wave receivers are harmonic converters; their linearity can degrade depending on the structure, LO drive, or other factors.5 Broadband receivers exist with effective IP3 levels in the range of 25 to 35 dBm. With receivers around 35 dBm, inherent third-order product levels are better than -90 dBm for tone levels of -10 dBm at the test port, which can be useful for all but the most linear DUTs. Figure 3 compares the third-order intercept point of two different receivers. One is a standard two diode, harmonic mixer being driven by a sinusoid and using the 12th harmonic. The other is a converter based on a nonlinear transmission line (NLTL) using a limited LO waveform with a high breakdown voltage sampler, operating on the 11th and 13th harmonics. The latter achieves better linearity and enables the measurement of more linear devices than the first converter.
Stimulus Issues: Source contamination can also play a role. Since many millimeter wave stimulus signals are multiplied, spurs are somewhat more of a concern than at lower frequencies. Because one knows the desired product locations, some clever frequency plan manipulation can avoid most problems. Multiplied phase noise is also a potential issue, particularly for smaller deltas. While a clean starting synthesizer is helpful, additional levels of correlation between stimulus and receiver synthesizers can improve the net measurement noise at small deltas.6
Leveling systems in the stimulus signal source sometimes create mysterious issues. Since combiner isolation is not perfect, particularly in broadband setups, the signal from one tone can leak over to the other tone’s sourcing path, enter its leveling detection system and mix with the other tone (see Figure 4). The resulting difference frequency (equal to delta) can be within the leveling loop’s bandwidth and remodulate as a sideband on the tone. Unfortunately, this sideband is in exactly the same location as a third-order product, leading to an IMD measurement error. Using a higher isolation combiner – or attenuators, if the measurement power requirements permit – can help. A system with a dynamic leveling loop bandwidth5 will also help minimize these effects, by not allowing the mixing product of the two tones to remodulate on the stimulus. In millimeter wave systems, the location of the leveling detection system varies greatly, and this can also play a role. More isolated detection paths augment combiner isolation and can minimize stimulus issues.

Figure 5 An improved leveling system and combiner allow a 15 kHz bias resonance to be identified with the PWR3 measurement.
To illustrate these effects, consider an amplifier that has a known bias system resonance near 15 kHz. This resonance could cause issues with close-in modulated performance, and it would be useful to identify it with an IMD measurement. The IMD measurement needs sufficient dynamic range at deltas on the order of the resonant frequency. Using a system with adequate leveling bandwidth control, phase noise and a high isolation combiner, the measured signature of the third-order product is shown by the blue diamonds in Figure 5. The DUT bias resonance is apparent. Using a different system with a lower isolation combiner (6 dB from a splitter), without leveling bandwidth control and with somewhat degraded phase noise, the data represented with triangles was measured. Noise was elevated at very low deltas, the measurement system signature was unintentionally obtained and the DUT response of interest was missed.
NET UNCERTAINTIES
The uncertainties discussed to this point can be combined with mismatch and repeatability to give some general estimates. The mitigation techniques discussed were employed, including a reasonably well-matched test system with ~15 dB return loss, full frequency list receiver calibrations, a high linearity receiver in the VNA and an improved stimulus system. The resulting uncertainty in product power at 100 GHz and DUT output tones of -10 dBm are shown in Figure 6. At higher product levels, the uncertainty is mainly a function of power accuracy. There is some delta dependency from multiplied synthesizer phase noise and a product level dependency from the signal-to-noise ratio.

Figure 6 PWRn uncertainty for a 100 GHz, –10 dBm tone with deltas of 10 and 200 kHz and 5 MHz.
The uncertainties in the other IMD metrics follow from the basic intermodulation product power measurement uncertainty (see Figure 6). The relative product measurement (IMn) and asymmetry measurement (ASYMn) are both the combination of two power measurements. One often assumes that these uncertainties will add on a root-sum-of-squares basis, although other methods are possible since correlations between the two measurements can vary.7 An intercept point (IPn) calculation is also basically the combination of two power measurements in a more complex form:

Again, one approach is to use a root-sum-of-squares basis but with the weighting factors implied in the equation. This is normally done in a linear form, rather than in dBm; if the uncertainties are small enough, the results will be numerically similar.

Figure 7 Amplifier third-order product measurement with 3 MHz delta, showing inferred uncertainty bounds.
The third-order power product of a millimeter wave amplifier was measured across 75 to 85 GHz, with a 3 MHz delta (see Figure 7). The implied uncertainties in the measurement are also shown. These bounds are in line with those shown in Figure 6, with some expansion at the higher frequencies where the absolute product level is dropping.
CONCLUSION
mm-wave IMD measurements have been explored from the viewpoint of potential measurement challenges that are exacerbated at the higher frequencies. Techniques exist, both procedural and with the equipment, to help improve the results and achieve uncertainties under 1 dB for modest product levels and deltas.
References
- W.J. Warren and W.R. Hewlett, “An Analysis of the Intermodulation Method of Distortion Measurement,” IRE Proceedings, Vol. 36, April 1948, pp. 4572466.
- F. Assadourian, “Intermodulation Distortion and Efficiency Analysis of Multicarrier Repeaters,” IRE Trans. Comm. Systems, Vol. 8, January 1960, pp. 68271.
- “Intermodulation Distortion,” Anritsu Application Note 11410-00213, April 2000 and “Intermodulation Distortion Measurements,” Anritsu Application Note 11410-00257, September 2000.
- J.S. Kenney and P. Fedorenko, “Identification of RF Power Amplifier Memory Effect Origins Using Third-Order Intermodulation Distortion Amplitude and Phase Asymmetry,” 2006 International Microwave Symposium Digest, June 2006, pp. 112121124.
- J. Martens, “Multiband mm-Wave Transceiver Analysis and Modeling,” 13thAnnual WAMICON Digest, April 2012, pp. 124.
- J. Martens, “On High Frequency/mm-Wave IMD Measurements with Small Tone Spacing,” 84thARFTG Conference Digest, Boulder, Colo., December 2014, pp. 125.
- “Evaluation of Measurement Data — Guide to the Expression of Uncertainty in Measurement,” Joint Committee for Guides in Metrology, 2008.
