Applying Error Correction to Network Analyzer Measurements

Applying Error Correction to Network Analyzer Measurements

David Ballo
Hewlett-Packard Co.,
Microwave Instruments Division
Santa Rosa, CA

Designers and manufacturers use network analysis to measure the electrical performance of the components and circuits destined for use in more complex systems. When these devices convey signals with information content, designers and manufacturers are most concerned with moving the signal from one point to another in the device with maximum efficiency and minimum distortion. Vector network analysis is a method of characterizing components accurately by measuring their effect on the amplitude and phase of swept-frequency and swept-power test signals.

Ideally, measurement systems would be perfect and provide completely accurate measurements. However, imperfections exist in even the finest test equipment and can cause less-than-ideal measurement results. Some factors that contribute to measurement errors are repeatable and predictable over time and temperature and can be removed, while other errors are random and cannot be removed. The process of network analyzer error correction is based on the measurement of known electrical standards, such as thru, open circuit, short circuit and precision-load impedance. Measurements of these standards provide knowledge about systematic errors in the test system. Once these errors are characterized, they can be removed mathematically from subsequent measurements.

The effect of error correction on data can be dramatic, as shown in Figure 1 . 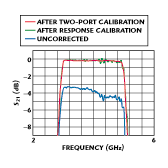Without error correction, measurements on this example bandpass filter show considerable loss and ripple. A simple error-correction technique such as response calibration removes the overall loss and frequency-response error. However, considerable measurement ripple still exists due to mismatch errors. (Mismatch errors are those due to nonperfect 50 W source and load matches.) The smoother, error-corrected trace produced by a two-port calibration subtracts the effects of all major systematic errors and illustrates the performance of the device under test (DUT) accurately.

This article describes several types of calibration procedures, including short-open-load-thru (SOLT) and thru-reflect-line (TRL). The effectiveness of these procedures is demonstrated in the measurement of high frequency components such as filters. Calibrations are also shown for those cases requiring coaxial adapters to connect the test equipment, DUT and calibration standards.

Types and Sources of Measurement Errors

All measurement systems, including those using network analyzers, can be affected by three types of measurement errors: systematic, random and drift. Systematic errors, as shown in Figure 2 , are caused 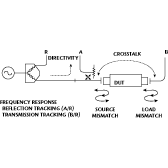by imperfections in the test equipment and test setup. If these errors do not vary over time, they can be characterized through calibration and removed mathematically during the measurement process. Systematic errors encountered in network measurements can be grouped in terms of signal leakage, signal reflections or frequency response. There are two error terms in each group for a total of six error terms. Signal leakage during transmission measurements is called crosstalk and is a result of finite isolation between the test ports.

Similarly, finite isolation of directional couplers or bridges within the network analyzer results in a leakage term during reflection measurements called directivity. Signal reflections are due to imperfect source and load matches of the test ports. (Load match refers to the match of the test port that is not supplying the measurement stimulus.) Unless the DUT has perfect port matches, reflections occurring between the DUT and test ports cause ripple in uncorrected transmission and reflection measurements.

Finally, frequency-response errors are associated with both transmission and reflection measurements. Since S-parameter measurements are always ratioed measurements (measured transmitted and reflected signals are divided by the incident signal), these errors are called tracking errors because they indicate how well the various receivers in the network analyzer track one another across a frequency sweep.

When the network analyzer reverses the direction of the measurement (that is, the source and load ports are swapped), a new set of six error terms applies. Therefore, the full two-port error model includes six terms for the forward direction and six terms (with different data) for the reverse direction for a total of 12 error terms. This situation is why two-port calibration is often referred to as 12-term error correction.

Random errors are inherently unpredictable so they cannot be removed by calibration. The main contributors to random errors are instrument noise (for example, sampler noise and the IF noise floor), switch repeatability and connector repeatability. When using network analyzers, noise errors often can be reduced by increasing source power, narrowing the IF bandwidth or using trace averaging over multiple sweeps. Proper care and handling of the RF connectors in the measurement system can minimize connector repeatability errors.

Drift errors occur when a test system's performance changes after a calibration has been performed. These errors are caused primarily by temperature variation and can be removed by additional calibration. The rate of drift determines how frequently additional calibrations are needed. Establishing a test environment with stable ambient temperature usually minimizes drift errors.

Types of Error Correction

Two basic types of error correction exist: response (normalization) and vector. Response calibrations are simple to perform, but correct for only a few of the 12 possible systematic error terms (specifically, reflection and transmission tracking). This process provides a normalized measurement by storing a reference trace in the network analyzer's memory. Subsequent measurements then are divided by this reference trace. Open/short averaging, a more sophisticated form of response calibration for reflection measurements, can be found on many scalar network analyzers. This technique averages two traces (one derived from measuring an open circuit, and the other from measuring a short circuit) to derive a reference trace.

Vector error correction is a more thorough method of removing systematic errors. This type of error correction requires a network analyzer capable of measuring (but not necessarily displaying) phase as well as magnitude, and a set of calibration standards with known, precise electrical characteristics. The vector error-correction process characterizes systematic error terms by measuring known calibration standards, storing these measurements within the analyzer's memory and using the data to calculate an error model of the test system. This error model then is used to remove the effects of systematic errors from subsequent measurements. Vector error correction can account for all major sources of systematic errors and permits accurate measurements. However, the process requires more calibration standards and more measurements than needed for response calibration.

Note that a response calibration can be performed on a vector network analyzer (in which case a complex (vector) reference trace is stored in memory) so that normalized magnitude or phase data can be displayed. However, this process is not the same as vector error correction (and not as accurate) because the individual systematic errors (all of which are complex or vector quantities) are not measured and removed.

One-port Calibration

The two main types of vector error correction are the one- and two-port calibrations. The one-port calibration technique was derived for use with one-port devices where only reflection measurements are possible. A one-port calibration can measure and remove three systematic error terms from reflection measurements (directivity, source match and reflection tracking). These three error terms are derived from a general equation that can be solved in terms of three simultaneous equations with three unknowns. To establish these equations, three known calibration standards must be measured, such as an open, a short and a load. (The load value is usually the same as the characteristic impedance of the test system Z₀ , generally either 50 or 75 W .) Solving the equations yields the systematic error terms, which then make it possible to derive the actual S₁₁ of the DUT from a reflection measurement.

When measuring two-port devices, a one-port calibration assumes a good termination on the unused port of the DUT. If this condition is met (for example, by connecting a high quality load standard), the one-port calibration is accurate. However, if port 2 of the DUT is connected to the network analyzer and both the forward transmission and reverse isolation of the DUT are low (for example, filter pass bands or low loss cables), the assumption of a good load termination often is not valid. In this case, two-port error correction can provide significantly better results than one-port error correction. An amplifier is a good example of a two-port device with an input match that can be measured accurately with one-port calibration. The reverse isolation of the amplifier prevents reflected signals due to the uncorrected load match of the analyzer from introducing measurement errors.

A reflection measurement of a terminated cable is shown in Figure 3 with and without one-port calibration. Without error correction, the classic ripple pattern appears, which is caused by systematic errors (primarily directivity error) interfering with the desired test signal. The error-corrected trace is much smoother and better represents the device's actual reflection performance.

Adapter Effects

Ideally, calibration for reflection measurements should be performed with a calibration kit that has the same type of connectors as the DUT. If adapters are necessary to make connections, the effects of these adapters then must be considered part of the measurement uncertainty. The reflection from an adapter that has been added to a network analyzer test port after a calibration adds to or subtracts from the desired DUT signal. This error often is ignored, which may not be acceptable. Here, worst-case effective directivity is the sum of the corrected directivity and the adapter reflection. For example, an adapter with an SWR of 1.5 will reduce the effective directivity of a test coupler to approximately 14 dB even if the coupler itself has infinite directivity. Thus, if an ideal Z₀ load is placed on the output of the adapter, the network analyzer would measure a reflected signal that was only 14 dB less than the reflection from a short or open circuit. Stacking multiple adapters compounds the problem. If adapters cannot be avoided, the highest quality types (with low SWRs) are always the best choice to reduce system directivity degradation.

Two-port Error Correction

Two-port error correction yields the most accurate results because it accounts for all six forward and all six reverse sources of systematic error. Once the system error terms have been characterized, the network analyzer derives the actual device S parameters from the measured S parameters. The mathematical equations used to derive the actual S parameters are such that each S parameter is a function of the other three S parameters. Therefore, the network analyzer must make both a forward and reverse test sweep and calculate all of the S parameters before updating any one S parameter.

When performing a two-port calibration, the part of the calibration that characterizes the crosstalk or isolation of the device often can be omitted. Crosstalk, which is signal leakage between test ports whether or not a device is present, can be a problem when testing high isolation devices such as a switch in the open position, or high dynamic range devices such as filters with a high level of rejection. Unfortunately, a crosstalk calibration can add noise to the error model because measurements often are made near the analyzer's noise floor. If isolation calibration is deemed necessary, it should be performed with a narrow IF bandwidth and trace averaging to ensure that the test system's crosstalk is not obscured by noise. In some network analyzers, crosstalk can be minimized by using the alternate sweep mode instead of the chop mode. (The chop mode performs measurements on both the reflection A and transmission B channels at each frequency point, whereas the alternate sweep mode turns off the reflection receiver during the transmission measurement.)

The best way to perform an isolation calibration is to place the devices that will be measured on each test port of the network analyzer with terminations on the other two device ports. Using this technique, the network analyzer views the same impedance vs. frequency during the isolation calibration as it will during subsequent measurements of the DUT. If this method is impractical (for example, in test fixtures or if only one DUT is available), then placing a terminated DUT on the source port and a termination on the load port of the network analyzer is the next-best alternative. The DUT and termination must be swapped for the reverse measurement. If no DUT is available or if the DUT will be tuned (which changes its port matches), then Z₀ terminations should be placed on each network analyzer test port for the isolation calibration.

Electronic Calibration

Traditionally, vector error correction is achieved by individual measurement of known, passive physical standards, such as opens, shorts and loads. The performance of these standards is guaranteed by extremely precise mechanical measurements. A solid-state calibration solution also is available that makes two-port calibration fast, easy and less prone to operator errors. The various impedance states in the calibration modules are switched with PIN-diode or FET switches so the calibration standards never wear out. The calibration modules are characterized at the factory using a coaxial TRL-calibrated network analyzer, making the HP ECal modules transfer standards (rather than direct standards). HP ECal provides good accuracy, typically with results better than SOLT calibration but somewhat less than a properly performed TRL calibration.

Estimating Measurement Uncertainty

Table 1 lists which systematic error terms are accounted for when using analyzers with transmission/reflection (T/R) and S-parameter test sets. Some straightforward techniques can be used to determine measurement uncertainty when evaluating two-port devices with a network analyzer based on a T/R test set. For example, Figure 4 shows a measurement of the input match of a filter after a one-port calibration has been performed. The example filter has 16 dB of return loss and 1 dB of insertion loss. The uncorrected load match of the network analyzer is specified to be 18 dB (although, typically, it's significantly better). The reflection from the test port connected to the output port of the filter is attenuated by twice the filter loss - in this case, only 2 dB. This value is not adequate to suppress the effects of this error signal sufficiently, which illustrates why low loss bidirectional devices are difficult to measure accurately.

To determine the measurement uncertainty of this example, it is necessary to add and subtract the undesired reflection signal (with a reflection coefficient of 0.100) to and from the signal reflecting from the DUT (0.158). To be consistent with the next example, the effect of the directivity error signal also is included. The measured return loss of the 16 dB filter may appear to be anywhere from 11.4 to 26.4 dB (-4.6 dB, +10.4 dB of uncertainty), allowing too much room for error. In production testing, these errors easily could cause filters that met specification to fail, while filters that did not meet specification could pass. In tuning applications, filters could be mistuned as operators attempt to compensate for the measurement error.

When measuring an amplifier with good isolation between output and input (that is, where the reverse isolation is much greater than the forward gain), much less measurement uncertainty exists because the reflection caused by the load match is severely attenuated by the product of the amplifier's isolation and gain. To improve measurement uncertainty for a filter, the output of the filter must be disconnected from the analyzer and terminated with a high quality load or a high quality attenuator is inserted between the filter and port 2 of the analyzer. Both techniques improve the effective load match of the measurement. An example, shown in Figure 5, places a 10 dB attenuator with an SWR of 1.05between port 2 of the network analyzer and the filter used in the previous example, thus improving the effective load match to 28.6 dB (-20log[10exp(-32.3/20) + 10exp(-38/20)]). This value is the combination of a 32.3 dB match from the attenuator and a 38 dB match from the network analyzer. (Since the error signal travels through the attenuator twice, the analyzer's load match is improved by twice the value of the attenuator.) The worst-case uncertainty now is reduced to +2.5 dB, -1.9 dB, instead of the +10.4 dB, -4.6 dB that exists without the 10 dB attenuator. While not nearly as good as what can be achieved with a full two-port calibration, this level of accuracy may be sufficient for many applications. Generally, low loss, bidirectional devices require two-port calibration for low measurement uncertainty.

Performing a Transmission Response Calibration

Response calibrations offer simplicity and speed, but with some compromise in accuracy. When making a filter transmission measurement using only response calibration, the first step is to make a thru connection between the two test ports (with no DUT in place). Thru calibration (normalization)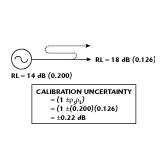 builds error into the measurement due to source and load match integration. For this example, test port specifications for the model HP 8711C network analyzer will be used. The ripple caused by this mismatch is calculated as ±0.22 dB and now is present in the reference data, as shown in Figure 6 . It must be added to the uncertainty when the DUT is measured to compute worst-case overall measurement uncertainty.

The same setup and test port specifications for the network analyzer can be used to determine the measurement uncertainty with the DUT in place. Three main error signals are caused by reflections between the ports of the analyzer and the DUT, as shown in Figure 7 . Higher order reflections can be neglected because they are small compared to the three main terms. One of the error signals passes through the DUT twice so it is attenuated by twice the insertion loss of the DUT. A worst-case condition occurs when all of the reflected error signals add together in phase (0.020 + 0.020 + 0.032 = 0.072). In this case, measurement uncertainty is +0.60/-0.65 dB. Total measurement uncertainty, which must include the ±0.22 dB of error incorporated into the reference measurement of the calibration, is approximately ±0.85 dB.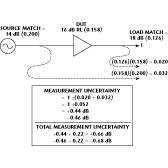

Another measurement-uncertainty example is an amplifier with 16 dB port matches, as shown in Figure 8 . The test setup and conditions remain essentially the same as in the case described previously, except now the middle error term is no longer present because of the amplifier's reverse isolation. This condition reduces the measurement error to approximately ±0.45 dB and the total measurement uncertainty to approximately ±0.67 dB (compared to ±0.85 dB for the filter).

Enhanced-response Calibration

A new enhanced-response calibration method requires the determination of short, open, load and thru standards for transmission measurements. The method combines a one-port reflection calibration and a transmission-response calibration to correct for the source-match error term during transmission measurements, something a standard-response calibration cannot do. The enhanced-response calibration, shown in Figure 9 , improves the effective source match during transmission measurements to approximately 35 dB (compared to 14 dB for normal-response calibrations). The calibration error is reduced from ±0.22 to ±0.02 dB and the two measurement error terms that involve interaction with the effective source match are greatly reduced. The total measurement error is ±0.24 dB instead of the previous value of ±0.85 dB for a standard-response calibration.

Transmission measurements are improved further by using the enhanced-response calibration method and inserting a high quality attenuator between the output port of the device and test port 2 of the network analyzer, as shown in Figure 10 . In this example, a 10 dB attenuator with an SWR of 1.05 is used (as with the reflection example). This process makes the effective load match of the analyzer 28.7 dB (approximately a 10 dB improvement). The calibration error is minuscule (±0.01 dB), and total measurement uncertainty is reduced to ±0.09 dB. This result is close to what can be achieved with two-port error correction. As illustrated, adding a high quality attenuator to port 2 of a T/R network analyzer can improve measurement accuracy significantly with only a modest loss in dynamic range.

Full Two-port Calibration

The example shown in Figure 11 calculates the measurement error after a two-port calibration and requires a vector network analyzer capable of measuring S parameters. The worst-case measurement errors for the filter have been reduced to approximately ±0.5 dB for reflection measurements and ±0.05 dB for transmission measurements. Phase errors are similarly small. These levels of measurement error are significantly lower than what can be achieved with simpler calibration techniques. The only drawback to full two-port calibration is that the measurement is at least twice as slow as compared to a one-port or response calibration since both a forward and reverse measurement must be made to calculate all four S parameters.

The most common way to perform two-port calibrations is to use SOLT standards. For measurements in coaxial environments, SOLT-based calibration is almost always the best choice. Recently, the upper frequency limit for SOLT calibration was extended with the introduction of a 1 mm connector, which allows accurate coaxial calibration standards up to 110 GHz.

TRL Calibration

Following SOLT in popularity, the next most common form of two-port calibration is TRL calibration, which is used primarily in noncoaxial environments at microwave frequencies (such as testing in waveguide environments, using test fixtures or making on-wafer measurements with probes). TRL calibration measures the same 12 error terms as SOLT calibration, although with different calibration standards and a slightly different error model. TRL has two variants: true TRL calibration, which requires a network analyzer with four measurement receivers; and TRL* calibration, which was developed for network analyzers with only three measurement receivers. Other variations of the TRL approach are based on different choices of calibration standards, such as line-reflect-match and thru-reflect-match.

True TRL calibration requires four measurement receivers (two reference receivers plus one each for reflection and transmission), and 14 measurements are made to solve for 10 unknowns. TRL* calibration assumes that the source and load match of a test port are equal - that there is true port-impedance symmetry between forward and reverse measurements. This premise is only a fair assumption for a three-receiver network analyzer. TRL* calibration makes 10 measurements to quantify eight unknowns. Both techniques use identical calibration standards.

In noncoaxial applications, TRL calibration achieves better source and load match corrections than TRL*, resulting in less measurement error since mismatch ripples are reduced. In coaxial applications, SOLT usually is the preferred calibration technique. While not used commonly, coaxial TRL can provide better accuracy than SOLT, but only if high quality coaxial transmission lines (such as beadless airlines) are used.

Calibrating Noninsertable Devices

When performing a thru calibration, the test ports typically mate directly. For example, two cables with the appropriate connectors can be joined without a thru adapter, resulting in a zero-length thru path. An insertable device is one that can be substituted for a zero-length thru. This device has the same connector type on each port but of the opposite sex, or the same sexless connector on each port. Either layout makes connection to the test ports quite simple. A noninsertable device is one that cannot be substituted for a zero-length thru. It has the same type and sex connectors on each port or a different type of connector on each port, such as 7/16 at one end and SMA on the other.

Several calibration choices are available for noninsertable devices. The first choice is to use a characterized thru adapter (electrical length and loss specified), which requires modifying the calibration kit definition. This technique will reduce, but not eliminate, source- and load-match errors. A high quality thru adapter (with good match) should be used since reflections from the adapter cannot be removed.

The swap-equal-adapters method is useful for devices with the same connector type and sex (for example, female SMA on both ends). It requires the use of two precision-matched adapters that are equal in performance but have connectors of different sexes. For example, for measuring a device with female SMA connectors on both ends using APC-7 test cables, the matched adapters could be a 7-mm-to-male-3.5-mm adapter and a 7-mm-to-female-3.5-mm adapter. To be equal, the adapters must have the same match, characteristic impedance, insertion loss and electrical delay. Many calibration kits include matched adapters for this purpose.

The first step in the swap-equal-adapters method is to perform the transmission portion of a two-port calibration with the adapter needed to make the thru connection. This adapter then is removed and the second adapter is used in its place during the reflection portion of the calibration, which is performed on both test ports. This swap changes the sex of one of the test ports so that the DUT can be inserted and measured (with the second adapter still in place) after the calibration procedure is completed. The errors remaining after calibration are equal to the difference between the two adapters. The technique provides a high level of accuracy, but not quite as high as the more complicated adapter-removal technique.

Adapter-removal calibration provides the most complete and accurate procedure for noninsertable devices. This method uses a thru adapter that has the same connectors as the noninsertable DUT. (This adapter is sometimes referred to as the calibration adapter.) The electrical length of the adapter must be specified within one-quarter wavelength at each calibration frequency.

Two full two-port calibrations are needed for an adapter-removal calibration. In the first calibration, the thru adapter is placed on test port 2 and the results are saved into a calibration set. In the second calibration, the adapter is moved to test port 1 and the resulting data are saved into a second calibration set. Two different calibration kits may be used during this process to accommodate devices with different connector types. To complete the adapter-removal calibration, the network analyzer uses the two sets of calibration data to generate a new set of error coefficients that eliminate the effects of the calibration adapter completely. At this point, the adapter can be removed and measurements can be made of the DUT directly.

Conclusion

Several different calibration techniques exist that can improve the accuracy of network analyzer measurements by removing the effects of systematic errors. Depending on the specifications of the device to be tested and the desired measurement uncertainty, the appropriate network analyzer and calibration type to achieve the best balance between measurement speed, accuracy and test system cost can be chosen.