Integrated Radar Receiver Front Ends

Integrated Radar Receiver Front Ends

Part two of a two-part tutorial series on radar front-end components follows. Part one appeared in the January issue of Microwave Journal and discussed low noise amplifier (LNA) characteristics for radar front-end applications. This article takes a broader look at the radar receiver front end and describes the overall characteristics of the components in an integrated front-end assembly. Frequency-tracking LOs are also described.

Ted Heil, Bill Roehrich and Jack Hakoupian
MITEQ Inc.
Hauppauge, NY

The system block diagram of moving target indicator (MTI) radars has not changed for many years. There has always been an input mixer to superheterodyne the received signal to an IF frequency where coherent processing detects a Doppler frequency shift of the received signal.

System Noise Figure and Dynamic Range

With the inclusion of the LNA, the role of the mixer in a radar front end has become more complicated. Before LNAs were used, there were no sources for receiver noise before the mixer; the first source of noise above the thermal noise floor was introduced after the frequency conversion in the IF amplifier. When an LNA is introduced ahead of the mixer, care must be taken that two sidebands of this noise are not converted into the IF band. If the unwanted sideband of noise is not suppressed, it will be converted or folded into the IF band with the desired sideband, resulting in a degradation in system noise figure by as much as 3 dB (if two equal sidebands of noise are added in the IF, degradation is 10 × Log₁₀ (2) = 3 dB). Figure 1 shows this image noise conversion.

Fig. 1: Image noise conversion.

The suppression of the unwanted sideband noise can be accomplished with an RF filter or through a conversion cancellation technique in an image-rejection mixer. Image-rejection mixers are more versatile than filters because they suppress the image conversion through phasing, allowing all image frequencies over an RF band that is greater than the desired IF bandwidth to be canceled. A filtered approach would require a tunable high Q filter or a dual-conversion configuration, which is not realized easily and is far from inexpensive.

Along with the use of image-rejection mixers in low noise radar receiver front ends, the improvement in input LNA noise figures has had another effect on the design of these front ends. To maintain that improvement in noise figure throughout the radar, higher front-end gain is required to ensure that the second-stage noise contribution is minimized.

The radar receiver example, shown in Figure 2 , reveals a system noise figure of 2.9 dB while the noise figure of the input LNA is only 1 dB, as shown in Table 1 . This degradation of 1.9 dB is due to second-stage noise figure contributions. In this case, the gain of the input LNA is not sufficient to minimize the noise contributions of the IF amplifiers. The obvious solution is to increase the gain of the LNA.

Fig. 2: The radar receiver example.

The increase in LNA gain reduces the contributions of the second stage to yield a cumulative noise figure of 1.1 dB, as listed in Table 2 . However, this increase in gain results in stressed dynamic range conditions, especially at the mixer. As a result, higher dynamic range mixers are now required to recover the overall system performance. The final system, listed in Table 3 , utilizes the high gain LNA combined with a high dynamic range mixer to produce the best combination of low noise and high dynamic range.

The vast majority of mixers are made from Schottky diodes. Because of the physics of the semiconductor, these mixers are limited in their linear operation. To achieve the input 1 dB compression point of +20 dBm, an LO drive of +27 dBm is required. Since most MTI radars use a three-channel monopulse feed, that individual drive level equates to almost 2 W of LO drive capability.

An alternative to the Schottky diode approach is to utilize ultra-high dynamic range mixers constructed from GaAs MESFETs. Each MESFET is configured in a passive switching configuration where the LO signal modulates the gate, switching the RF between drain and source. Since the MESFET's operation is linear, the harmonics and two-tone spurs will be low. But also, since high level signals can be switched with relatively low gate voltage, the MESFET becomes an efficient mixer. A C-band radar front end has been developed that utilizes a mixer operating with +8 dBm of LO power and has an input 1 dB compression point of +12 dBm. That performance translates to an LO power requirement of +16 dBm per mixer, which is much more achievable and cost effective than +27 dBm.

Phase and Amplitude Tracking

In addition to providing the low noise downconversion of the received signals, the receiver front end in monopulse systems typically must also retain the phase relationship between three inputs (sum, azimuth and elevation channels). Typically, phase and amplitude tracking values are specified over the entire RF band. At C-band, phase and amplitude tracking values are typically ±0.5 dB and ±5°, respectively, although tighter tracking is now available based upon the use of broader band, lower Q components.

Front-end Design Responsibility

Traditionally, front-end integration problems were the responsibility of the radar system's engineer. However, the burden of front-end design has shifted recently to the microwave components manufacturer. This shift in responsibility is due mainly to the added sophistication in design and construction required to meet the next-generation performance goals. The microwave engineer who designs LNAs and mixers has more freedom while integrating the system. He or she can shift design priorities between the components in the chain to achieve the overall specifications. For example, if a system dynamic range is extremely difficult, the input-stage gain can be lowered. However, to maintain the overall noise figure, the mixer loss and second-stage amplifier noise may be lowered.

This modification is a different approach to increasing the dynamic range of the system but, in the microwave world, there are many ways to accomplish the same objective. This flexibility is afforded to the microwave designer but not usually to the systems engineer who does not realize these problems exist until after the hardware is delivered. Additionally, there are areas that are almost impossible to model. The most difficult area to predict is the effect of SWR interaction between the components. A systems engineer can approximate the cumulative cascaded SWR performance through modeling techniques. However, the phase of the reflection coefficients can almost never be predicted. Typically, this unknown phase characteristic is treated as a random variable and a wide range of possible outcomes are predicted. In reality, the systems engineer can only try to pad the effects of interaction, but this approach is lossy and will impact other parameters. The microwave engineer can introduce matching elements on an integrated assembly that will provide performance much closer to the theoretical values. In any case, even when black box specifications are defined to the microwave engineer, close communication with the systems engineer is critical to ensured success.

Improving MTI Processing

Since an MTI radar uses Doppler frequency shifts to separate small moving targets from fixed clutter, the phase coherency between the transmitted signal and the downconverted received signal is of extreme importance. Most existing ground-based radars use high power magnetrons to generate the transmit signal. These sources are not phase coherent from pulse to pulse and suffer from significant frequency instabilities. Receivers use stand-alone LOs to convert the return signal to an IF frequency (typically 30, 60 or 160 MHz) where the coherent processing is performed. Usually, this LO signal is generated by a VCO or synthesizer and, as a stand-alone source, is neither tracked nor coherent to the transmitting magnetron.

Frequency Tracking

How the receiver LO tracks the frequency drift of the magnetron must be considered. To accomplish this tracking, the receiver LO is locked to the magnetron frequency by an automatic frequency control (AFC)/stable LO (STALO) (VCO) loop, as shown in Figure 3 . The AFC circuit mixes a sample of the transmitted signal with a sample of the receiver LO. The two samples are separated by the IF frequency plus some amount of tracking error. The error is determined by the AFC circuit and fed back to the receiver LO in a continuous fashion until the error is minimized to within the specified tracking accuracy. In certain cases, a VCO is used because of its ability to track the magnetron quickly. If speed is not critical and phase noise is, then a phase-locked synthesizer (STALO) is used. The optimum system will use a dual-mode source that utilizes a VCO for fast tuning and a synthesizer for high stability and fine tuning.

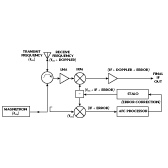Fig. 3: An MTI radar with an AFC/STALO (VCO) loop.

Existing MTI radars have used this approach for years with analog feedback circuits that include an open-loop frequency discriminator. The performance inaccuracies of these open-loop AFC circuits limit the clutter-rejection capabilities severely. However, advanced digital versions include extremely complicated phase-locked loop circuits to achieve high tracking accuracy. In addition, these newer AFCs use several sweep modes to acquire the signal, fine tune the error and hold the offset constant over transmit dead time. Today, with high speed digital processing and phase-locked AFC circuits, the performance of these AFC/STALO loops has improved tremendously. Upgrades of existing radars to new digital AFCs are common because of their extremely attractive cost-to-performance ratio.

Phase Coherency

In addition to tracking the magnetron's frequency instability, the receiver also must track the phase for coherent Doppler processing. Figure 4 shows how the receiver generates a reference that is phase coherent with the transmit signal. Since the magnetron is basically an oscillator that is pulsed on and off to generate the transmit signal, the transmit signal's phase will be random from pulse to pulse. In coherent Doppler processing, the received signal must be compared to a signal that is phase coherent with the transmitted pulse. To accomplish this comparison, circuits must be used to memorize the phase of the magnetron for each transmitted pulse. The memory function is performed by an injection-locked coherent oscillator (COHO) that stores the phase relationship of the transmitted pulse.

Fig. 4: An MTI radar with a COHO loop.

The COHO will hold the phase relationship of the magnetron for a period of time, long enough to process the return from the referenced pulse. Recent advances in this oscillator technology have resulted in errors as low as 0.75° RMS phase jitter with respect to the magnetron pulse for a period of up to 1.5 ms after the transmit pulse.

Appendix A lists the digital AFC/STALO/COHO specifications achievable today. These specifications are based on hardware produced for a US Navy tracking radar upgrade system, which included a tuned prereceiver and VCO-based AFC circuitry.

Conclusion

Although the basic MTI radar configuration does not change substantially, the proper selection of components will optimize system performance. The combination of a high gain LNA and a MESFET image-rejection mixer can provide both low overall system noise and good dynamic range. In the front end, the LO must track the transmit magnetron's phase and frequency for proper Doppler detection. An AFC/STALO (VCO) loop integrated into the front end provides this phase-tracking capability. The selection and integration of these components can be best made by the microwave component manufacturer and supplied in the form of a complete radar front-end assembly. The result is a compact MTI radar receiver front-end design that provides state-of-the-art system performance.