Wireless communication gadget users nowadays tend to pursue more convenience, such as multi-functions and higher mobility. The former results in a multi-band service oriented device; the latter drives the development of reduced size equipment. Thus, the roles and expectations of RF components are becoming more challenging. In particular, quality filters and couplers are required to be designed by cutting-edge technology. With regard to overcoming the limitations in the current design capabilities and going beyond the boundary, a number of techniques have been exploited. New alternative approaches have been sought, and the concept of metamaterial structures has started to draw a lot of attention.

A composite right-/left-handed (RH/LH)transmission line (CRLH) has been studied for microwave component design. Among these metamaterial applications, the zero-order resonance (ZOR) concept is a valuable key of size reduction methods. The ZOR of no phase variation between two ports is presented based on a one unit cell;1-3 a CRLH transmission line with 24 cells shows an infinite wavelength.4 The ZOR and the negative resonance have been realized in the form of multi-cells of a rectangular patch with a shorting pin or a metal strip next to split ring resonators (SRR) under the name of the CRLH-TL structure. Since the multiple cells have one size and are repeated over a lengthened area, they have periodic stop- and pass-bands at integer multiples of the fundamental frequency, which possibly lowers the freedom of design.4-5 In this article, a new design methodology using a modified circular mushroom structure is suggested for ZORs, and a gap between the ZORs is used as a capacitive coupling element for implementing the target bandpass filtering.
Theory and Design
A bandpass filter is designed on the basis of the specifications shown in Table 1. The transfer function, a mathematical expression, which best fits the amplitude of the required frequency response, must be known, because the transfer function will be manipulated by the coupling between the resonators in the prototype circuit. The transfer function is given in Equation 1

where s = jw and w = 2pf is the angular frequency.

Figure 1 Conventional and metamaterial prototype circuits of the bandpass filter: (a) conventional circuit, (b) frequency response, (c) DNG CRLH-TL equivalent circuit and (d) ENG-TL equivalent circuit.

Figure 2 A full circular mushroom structure.
It is then converted to a prototype, whose schematic is shown in Figure 1. As is typical for a classic filter, it comprises a series capacitance coupling two identical parallel resonators. After the circuit is simulated, the frequency response is obtained, where S21 meets the specifications from Table 1. For the same frequency response, this conventional filter can be changed to a metamaterial-version, like the double negative (DNG) or the epsilon negative (ENG), whose zero-order resonance renders size-minimization and performance-improvement very effectively.1-4 In other words, if the dispersion diagram of a DNG or ENG equivalent circuit is obtained and the phenomenon at its ZOR is considered. The no-phase variation effect will set the size of the resonator free from a half-wavelength resonance condition and this possibly results in size reduction.

Figure 3 ZOR and its RH integer harmonics of a full circular musroom structure: (a) ZOR around 3 GHz and (b) electric field distribution of the ZOR.
The DNG is found by dividing the conventional prototype circuit into the RH and LH parts and making their propagation constants of the same magnitude but out-of-phase. The ENG is obtained by making both the effective capacitance and effective inductance of the resonators become zero and positive, and making their zero crossing point coincide with the aimed center frequency. As addressed earlier, this article uses a circular mushroom or its modification as the resonator and is the basis for implementing a bandpass filter. Considering a circular mushroom (see Figure 2), it consists of a full circular patch supported by a metal shorting pin connecting the patch and the ground. Without a gap from a feeding port, the circular mushroom itself can become an ENG rather than a DNG. If the full circular mushroom has gaps at the ports, it is the DNG. When a full circular mushroom is split to two half circular mushrooms by a gap, each of the two half circular mushrooms is an ENG, though the two half circular mushrooms with a gap can be interpreted as the DNG.
Again, if a full circular mushroom is connected to the input and output ports, the metallic patch, the substrate spacing and the shorting pin are interpreted as the series inductance, shunt capacitance and shunt inductance loading of an ENG circuit, respectively. This full circular mushroom was simulated by a 3D EM analysis, with the dielectric constant = 4.4, the height = 1.27 mm and the circular patch diameter = 20 mm. The frequency response is shown in Figure 3. As shown, the full circular mushroom has a ZOR with the in-phase electric field distribution over the whole structure, and its right-handed (RH) spurious harmonics in the frequency response. Also, if the number of cells of full circular mushrooms was extended to make a bandpass filter, it would work against an effective size reduction. In order to overcome the drawbacks of using full circular mushrooms, half circular mushroom resonators to minimize the physical size and a coupling element between the resonators to enlarge the stopband are considered, as shown in Figure 4.

Figure 4 Half circular mushroom resonator (a) and its ENG circuit model (b).

Figure 5 S-parameters (a) and dispersion diagram (b) of a half circular mushroom ZOR.
The equivalent circuit of a one half circular mushroom resonator is determined to meet the performance of ZOR at 3 GHz and all its elements are calculated: LR1 = 6 nH, LR2 = 11 nH, CR = 4.8 pF and LL = 0.7 nH. According to this resonator circuit, the frequency response and the dispersion diagram of a half circular mushroom resonator are shown in Figure 5. S21 has its resonance at 3 GHz, but the bandwidth and the return loss are very poor, because a one half circular mushroom is just a resonator having a ZOR, not a bandpass filter. To make a complete bandpass filter, another coupled half circular mushroom resonator is needed.
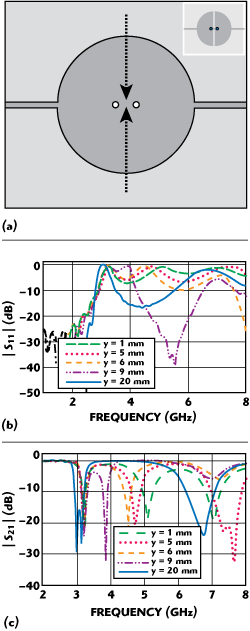
Figure 6 Coupling two half circular ZORs: (a) creating the two half circular mushrooms, (b) S11 as a function of slit length and (c) S21 as a function of slit length.
When two half circular mushroom ZORs are put together with a coupling element, there are roughly three factors to adjust the coupling between the resonators: the slit gap, the slit length and the positions of the shorting pins. These factors have been varied to find the most appropriate values. In this particular design, among the number of coupling factors, just the slit length has been varied with the others fixed. From Figure 6, it is noted that the complete cut of the circle gives an acceptable performance. After undergoing further parameter studies, the optimized filter structure is found.
The gap between the two half circular resonators and the distance of their shorting pins have been adjusted to form a passband centered at 3 GHz, with the closest spurious frequency component far apart. Actually, another passband is seen at approximately 7 GHz, and to make sure this new filter has a wider stopband for good isolation, a pair of impedance matching elements is placed at the input and output ports, as shown in Figure 7. The proposed design results in a frequency response agreeing with the specification, 200 MHz bandwidth with insertion loss < 1 dB and RL better than 20 dB, with stopband > 2 GHz, checked with the 3D EM simulation. Using this verified proposed design method, the filter was fabricated and the measurements show good agreement with the simulation, except for the shift in frequency and magnitude due to the discrepancy between the actual and ideal substrate, as shown in Figure 8.
Finally, a comparison is made to show the strengths of the proposed filter over the full circular mushroom BPF in terms of size and isolation. Compared to the 2nd order full circular mushroom BPF, the proposed 2nd order half circular mushroom BPF is more than half in size and has a wider stopband.

Figure 7 Performance of the proposed metamaterial bandpass filter: (a) geometry, (b) simulated frequency response, (c) ZOR field, (d) fabricated filter and (e) measured response.

Figure 8 Finalized metamaterial bandpass filter with a two coupled half circular mushroom ZOR: (a) photograph and (b) performance.
Conclusion
Half circular mushroom cells were used as the ZORs and a gap was introduced as coupling between neighboring ZOR resonators. A size reduction better than half that of a full size circular mushroom is achieved along with an improved stopband, compared to the full circular mushroom case or conventional filters based upon half-wavelength resonators.
Acknowledgment
This work is supported by the University of Incheon Research Promotion Program.
References
- S. Kahng and J. Ju, ”Design of the UWB Bandpass Filter Based on the 1 Cell of Microstrip CRLH-TL,” 2008 IEEE International Conference on Microwave and Millimeter Wave Technology Proceedings, Vol. 1, pp. 69-72.
- S. Kahng and J. Ju, “Realized Metamaterial CRLH Bandpass Filter for UHF-band WLAN with Harmonics Suppressed,” 2008 IEEE MTT-S International Microwave Symposium Workshop on Art of Miniaturizing RF and Microwave Passive Components, pp. 98-101.
- S. Kahng and J. Ju, “Design of a Dual-band Metamaterial Bandpass Filter Using Zeroth Order Resonance,” Progress in Electromagnetics Research C, Vol. 12, March 2010, pp. 149-162.
- C. Caloz and T. Itoh, Electromagnetic Metamaterials: Transmission Line Theory and Microwave Application, John Wiley & Sons Inc., Somerset, NJ, 2006.
- R Marques, et al., Metamaterials with Negative Parameters: Theory, Design and Microwave Applications, John Wiley & Sons Inc., Somerset, NJ, 2008.
Geonho Jang received his BE degree from the University of Incheon, Incheon, Korea, in 2009. He is currently working toward his MS degree in radio science and engineering in the department of information and telecommunication engineering at the University of Incheon. His interests include microwave components, antennas and metamaterials.
Sungtek Kahng received his PhD degree in electronics and communication engineering from Hanyang University, Korea, in 2000, with a specialty in radio science and engineering. From 2000 to early 2004, he worked for the Electronics and Telecommunication Research Institute on numerical electromagnetic characterization and developed RF passive components for satellites. In March 2004, he joined the department of information and telecommunication engineering at the University of Incheon, where he has continued research on analysis and advanced design methods of microwave components and antennas including metamaterial technologies and wireless power transfer.
