In the late 1970s, when one of the authors (Rautio) first got started in microwaves, one of his first tasks was to design filters on alumina for Landsat IV. The design was carefully performed using the commonly assumed substrate dielectric constant of 9.8. Even so, several design iterations were required. “Get used to it,” he was told. “Multiple design iterations are a fact of microwave design life.” Or so it was thought.

Fast forward to 2007. EM analysis is a mainstream design tool. Dielectric Laboratories (Casenovia, NY) is having good success with rapid fire design of filters using commercial, 3D planar EM analysis. Success on first fabrication is now normal, except for certain cases. The troublesome cases use a nearly exactly zero temperature coefficient ceramic, and that ceramic is anisotropic. Figure 1 illustrates the problem. For this filter, pretending that the substrate dielectric constant is isotropic means a re-design is required. With anisotropy included, the filter is ready for production.¹

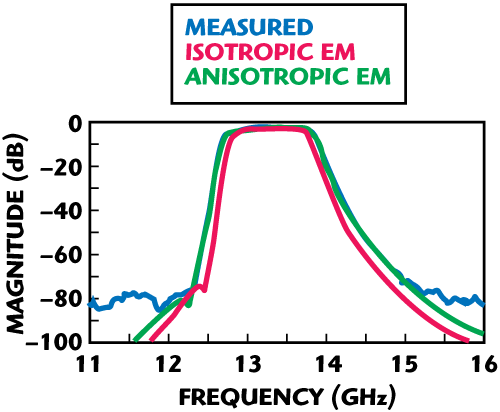
Figure 1 Measured vs. calculated performance of a filter.

Anisotropy means that the dielectric constant depends on the direction of the electric field. The obvious work-around for not being able to analyze anisotropy using EM is to assume a constant dielectric constant in all directions (isotropy) and to use an average dielectric constant. A percentage of a transmission line’s electric field is parallel to the substrate surface and the rest is perpendicular to the substrate surface. Therefore, a weighted average of the horizontal and vertical dielectric constants is used, and the average is weighted according to the percentage of horizontal and vertical electric fields.

This works well as long as only single transmission lines are used, all with the same width. If the width is changed, the percentage of horizontal and vertical electric field has to be changed as well. A different weighted average is needed. If the difference is not so large, maybe just one isotropic dielectric constant can be used and one can still get the designs to work.

Assuming Isotropy Fails for Filters

The big problem comes with filters. The resonant frequencies of the resonators in filters are determined mostly by the vertical dielectric constant. In order to get the right center frequency for the filter, one can simply use the vertical dielectric constant and pretend that the substrate is isotropic. However, there is more to a filter than the center frequency; the bandwidth must also be nailed down. The bandwidth depends on the coupling between resonators, which depends on the horizontal dielectric constant. However, the horizontal dielectric constant is different.

Thus, if an anisotropic substrate is actually assumed to be isotropic, the center frequency or the bandwidth can be right but both cannot be right at the same time. This was the situation faced by Dielectric Laboratories, resulting in the “Isotropic” and the “Measured” data shown in the figure. This amount of error absolutely requires a second design iteration, “stretching” the filter to an artificially wider target bandwidth, hoping that the actual realized bandwidth would end up close to requirements.

To address this problem, Sonnet modified its software to include anisotropy. Specifically, the capability to analyze “uniaxial” anisotropy was added. In other words, there is one horizontal dielectric constant for all horizontal field directions and a different dielectric constant for the vertical field direction. Dielectric Laboratories plugged the measured values for the substrate’s anisotropy into the simulation using the modified software, which resulted in the “Anisotropic” curve.

Anisotropic Ceramic? Ridiculous!

It seems really strange. How can a ceramic possibly be anisotropic? Some kind of material is ground (sapphire is used to make alumina), and then all the randomly oriented grains are melted together. Even if the original material is anisotropic (as is the case with sapphire), the resulting ceramic should be almost perfectly isotropic. Not quite. The above reasoning works only when the grains of the ceramic are spherical. In general the grains are not spherical and the “random” orientation of the grains in the ceramic has preferences. This makes most ceramics anisotropic. For example, in the only published measurement of anisotropy in alumina that was found,² the dielectric constant was determined to be 8.607 vertically and 10.159 horizontally (manufacturing variability was not investigated). The usually assumed 9.6 to 9.9 represents a nice average of the two measured values, but the difference between the average dielectric constant and the true anisotropic dielectric constant easily explains the multiple design iterations on those Landsat IV filters.

To see why a ceramic can be anisotropic, look at Figure 2, which illustrates a hypothetical substrate. The dark cylinders have high dielectric constant and the light areas are low, and half of the total volume is devoted to each type. For the top example (2a), the total capacitance from top to bottom is dominated by the high dielectric constant. This is just like connecting two capacitors in parallel. The total capacitance is dominated by the larger capacitor.

Next, look at the middle example (2b). Here each material still takes up the same percentage of the substrate volume. The total capacitance between the terminals is now dominated by the low dielectric constant. This is similar to connecting two capacitors in series. The smaller capacitor controls the total capacitance. The actual situation is similar to example (2c). When the ceramic grains are not spherical, then the higher dielectric constant dominates for electric field parallel to the length of the grains and the lower dielectric constant dominates for electric field parallel to the shorter grain dimension. Thus, any ceramic that has non-spherical grains will have grains tending to be preferentially oriented and is necessarily anisotropic even if the grains themselves might be perfectly isotropic.

Not only are most ceramics anisotropic, composite substrates are anisotropic too. Composite substrates are formed of at least two different materials; for example, PTFE and glass fiber. The reason for two materials is so the substrate temperature coefficient matches that of the copper foil cladding. The two materials are selected for strength and durability. Each of the materials has a different temperature coefficient and they are mixed and formed so that the net temperature coefficient matches that of copper. The substrate dielectric constant then also becomes a weighted average of the two materials, which is also necessarily anisotropic for the same reason that ceramics are anisotropic, as described above.

How about semiconductors? Some common microwave RFIC semiconductors are anisotropic. Yet they are designed as if they were isotropic. With so much time and money at stake (cost of failure is very high), why is this done? Because the numbers for the semiconductor anisotropy are not known. At least now they can be measured. Once measured, the anisotropy failure risk can then be removed from the planar EM design cycle.

Just Tell Me the Answer!

So now the fact that most substrate materials are anisotropic is known, the EM analyses including the effect of anisotropy can be done. What is missing? Measurements of anisotropy. There are many ways to measure anisotropic dielectric constants and most of them require substantial effort. A technique has been developed^2–5 that requires initial setup effort and sample preparation. Once this is done, measurements may be taken and reduced to anisotropic dielectric constants repeatedly and quickly.

Let us start with results. Table 1³ shows results for two samples (R1 and R2) of FR4 (the popular PCB material used for computer boards, a glass fiber weave loaded epoxy) up to 2 GHz. Figure 3 shows results for one sample of Rogers RO3010® laminate, a ceramic loaded PTFE substrate up to 10 GHz. It was expected that the horizontal dielectric constant would be higher than the vertical dielectric constant. For FR4, that is not the case. Also note that the FR4 measurement shows considerable dispersion, with the horizontal starting low and the vertical starting high. At higher frequencies, they are almost equal.

This suggests that the reason the horizontal dielectric constant is low is because of how the dielectric constant is measured. The procedure starts by fabricating a microstrip (or stripline) resonator and measuring the resonant frequencies. Then, several EM analyses of the same resonator are performed assuming a reasonable value for the dielectric constant. For FR4, a reasonable guess is 4.0. Next, the EM analysis resonant frequencies are compared to the measured ones. For example, if the EM analysis says a dielectric constant of 4.0 should give a resonant frequency of 1.00 GHz, but a resonant frequency of 1.01 GHz is measured, the dielectric constant of the measured substrate is approximately 2 percent lower, or 3.92. (Resonant frequencies vary inversely with the square root of the dielectric constant, which is why a delta in frequency of 1 percent requires a change in dielectric constant of 2 percent.)

The above approach works great for isotropic substrates, but anisotropic materials are considered here. It turns out that exactly the same approach just described can be used, except that a coupled line “RA” resonator is now built and measured, one end of which is shown in Figure 4. The fine meshing required for accurate EM analysis is also shown. The entire resonator (which extends down and to the left) is nearly 25 wavelengths long. The vertical dimension is magnified 8 times. The lines are 0.050 inch wide with a 0.025 inch gap. The RA resonator has two resonances for each half wavelength of length: An even and an odd mode. The even mode (current flows in the same direction on both lines) resonance is strongly dependent on the vertical dielectric constant; the odd mode (current flows in opposite directions) also depends on the horizontal dielectric constant. Two EM analysis cases are now run using selected anisotropic dielectric constants. By comparing the EM analyzed even and odd mode resonant frequencies to the measured even and odd mode resonances, the anisotropic dielectric constants that underlie the measured resonator can be reverse-engineered. This is how the data of Table 1 and Figure 3 has been obtained. Details and complete theory are described in the literature.^2–5

The key point is that the odd mode depends strongly on the horizontal dielectric constant. The horizontal electric field of the odd mode is at the top surface of the substrate in the gap between the two lines. If this region of the FR4 substrate is mostly epoxy, then the lower dielectric constant of epoxy dominates the odd mode resonances. This could have caused the horizontal dielectric constant to be lower than the vertical. If true, then this lower value of horizontal dielectric constant should be used for EM analyses of coupled lines on this substrate. If the bulk value of the horizontal dielectric constant was measured, it would be higher and would give bad EM analysis results for coupled lines, because the coupled line odd mode does not see the bulk horizontal dielectric constant; it sees only the horizontal dielectric constant right at the surface of the substrate.

Note also that the dielectric constants of the two samples (R1 and R2) are slightly different. This suggests that this might also be due to the fiber glass weave. For example, if the gap between the lines were close to a strand of the glass weave, then the horizontal constant will be higher. Since these measurements are quickly performed once the resonators are fabricated, statistical studies can be easily realized providing variability information, useful for yield analysis.

Measuring Rogers RO3010 Laminate

To further verify the measurement technique, resonators on Rogers RO3010 material were fabricated and measured by Rogers. The measured substrate dielectric constants were extracted by Sonnet. This substrate material is a ceramic loaded PTFE. On the scale of the resonator, the material is perfectly homogenous. Because the microscopic ceramic grains are not spherical, it is also anisotropic. Bulk measurements of this material verify that the horizontal dielectric constant is indeed higher. As can be seen in Figure 3, the measurements can be confirmed. The measured dielectric constants are approximately 11.0 vertical and 11.9 horizontal. One might wonder why these measured values are both somewhat higher than the quoted value of 10.3 for this substrate. The reason is that substrate manufacturers use industry standard techniques for measuring dielectric constants.⁶ It turns out that those methods were not developed by microwave engineers. They were developed by quality control engineers for batch-to-batch consistency, well prior to the advent of accurate EM analysis. Consistent measurement was critical and was achieved. Accurate measurement was not. Those results were never intended to be used for high accuracy EM analysis. The high accuracy results obtained for dielectric constant are intended for exactly that use and are consistent with the modern-day experience of microwave designers using these materials.

Getting Lots of Data

One might wonder how the dielectric constants are measured at so many frequencies. Generally, resonator techniques obtain the dielectric constant at one frequency. For multiple frequencies, multiple resonators must be fabricated. Not so for this technique. One very long resonator is simply built and multiple higher order resonances are used to measure the dielectric constant at multiple frequencies. For the FR4 case, the resonator is 10 inches long and eight even/odd mode resonance pairs are measured for vertical/horizontal dielectric constant determinations at eight frequencies. At 2 GHz, the resonator is four wavelengths long.

The Rogers RO3010 laminate RA resonators are 9.5 inches long and nearly 50 even/odd mode resonance pairs are measured, which determine vertical/horizontal dielectric constant pairs at nearly 50 frequencies up to 10 GHz. The resonator is nearly 25 wavelengths long. Recall that EM analysis is used to determine how even/odd mode resonant frequencies map into the underlying vertical/horizontal dielectric constants. Extreme accuracy for the EM analysis is absolutely critical for success in this effort. For example, extremely fine meshing is required. A major portion of this effort has been to quantify and bound all possible error sources in this measurement. In fact, substantially more effort has been expended in error analysis than in the actual measurement itself. As a result of this detailed error analysis it can be said with confidence that the values obtained for both dielectric constants are accurate to nearly a full four digits, with the horizontal dielectric constant showing slightly more error than the vertical. Details are shown in the literature.^2–5

What Could Go Wrong?

The most likely failure mode in duplicating this work will be failure of the EM analysis to provide sufficiently accurate resonant frequencies. Accuracy to a few ten’s of kHz is required, even for the resonances at 10 GHz. Not only is very fine meshing (for both subsection length and subsection width) required, but also the EM analysis must have extremely accurate evaluation of the “Green’s function”.

In short, the Green’s function is the coupling between subsections as calculated by the EM analysis. For example, given 1.0 Ampere on one subsection, the EM analysis might calculate that 3.372528412 V is induced on another subsection. This calculation is repeated for every possible pair of subsections in the entire circuit. The results fill a big N×N matrix, where N is the number of subsections. Since this calculation can be time consuming, some EM analyses take a short-cut and calculate this number out to only three significant digits. While such an EM analysis might provide a fast result, it is unlikely to be usable for this application.

The Sonnet EM analysis, which is used here, calculates the Green’s function to full numerical precision at all times. This is possible because the technique used performs the full precision Green’s function calculation almost instantly as it is needed. There is no pre-calculation or pre-storage of the Green’s function required. Figure 5 shows the measured response of the nearly 25 wavelength-long resonator compared to analysis for the top two GHz (8 to 10 GHz) of the resonator, where the maximum difference between measurement and analysis occurs. With results like this, filters and amplifiers can now be designed with confidence.

Substrate anisotropy can now be accurately measured and included in the planar circuit design flow. This eliminates one of the few remaining major design failure risks and uncertainties, even for tight design requirements. Pretending that substrates are isotropic is history.

RO3010® is a registered trademark of Rogers Corp.
Sonnet® is a registered trademark of Sonnet Software Inc.

References
1. J.C. Rautio, “Shortening the Design Cycle,” IEEE Microwave Magazine, Vol. 9, No. 6, December 2008, pp. 86-96.
2. J.C. Rautio, “A Proposed Uniaxial Anisotropic Dielectric Measurement Technique,” 2009 International Microwave Workshop Series 2009, Guadalajara, Mexico, February 19-20, 2009, pp. 59-62.
3. J.C. Rautio and S. Arvas, “Measurement of Planar Substrate Uniaxial Anisotropy,” IEEE Transactions on Microwave Theory and Techniques, Vol. 57, No. 1, Part 1, October 2009, pp. 2456-2463.
4. J.C. Rautio, “Measurement of Uniaxial Anisotropy in Rogers 3010 Substrate Material,” accepted for publication IEEE COMCAS, 2009.
5. J.C. Rautio and B.J. Rautio, “High Accuracy Broadband Measurement of Anisotropic Dielectric Constant Using a Shielded Planar Dual Mode Resonator,” accepted for publication ARFTG, December 2009.
6. S.J. Normyle, “ASTM D3380–85 Standard Test Method for Permittivity (Dielectric Constant) and Dissipation Factor of Plastic-based Microwave Circuit Substrates, Section 10,” West Conshohocken, PA; ASTM, 1985, Vol. 10.02, Annual Book of Standards.