Harmonic balance simulation is a fast and effective means for accurately predicting the steady-state performance of RF, microwave and millimeter-wave circuits. Transient simulation is also important for predicting the time-domain behavior of many of these circuits, especially when they include oscillators, frequency dividers and mixed-signal functions. Several SPICE-based circuit simulators include cutting-edge model libraries for nonlinear devices, such as field effect transistors (FET), bipolar transistors and diodes. Yet most SPICE simulators lack accurate and effective modeling solutions for the distributed components so common in high frequency design. The extensive substrate-specific and electromagnetic (EM)-derived models that are available with harmonic balance are typically described in the frequency domain. Achieving equivalent behavior for these models when used in time-domain SPICE simulations is a challenging endeavor. This article describes a successful modeling and transient simulation approach, achieved with the use of a high frequency design tool suite that offers extensive and accurate models, integrated with a highly accurate, SPICE-based circuit simulation tool. The result is accurate transient simulations for circuits containing coupled transmission lines, discontinuities and components characterized by frequency-dependent multiport parameters obtained from numerical EM analysis.
Transient Simulation of Distributed Networks with Dispersion
As design frequencies increase, so does the need for accurate modeling of distributed elements. These elements may form intentional design components, such as filter structures or matching networks, or they may represent the unintentional parasitic effects extracted for an interconnect system. In either case, an effective modeling approach is to partition the overall distributed network into single and coupled transmission lines, with separate models for discontinuities such as bends, steps in width, tee-junctions and crosses. Transmission lines are known to satisfy the telegrapher’s equations, which (in the time domain) are given by

Transient simulation with constant values for R, L, G and C is therefore a fairly straightforward process. However, dispersion, skin effect and dielectric losses all contribute to significant frequency dependencies in the RLGC values. EM solvers of various degrees of accuracy, ranging from 2D quasi-static to 3D full-wave, can extract these RLGC values and their frequency dependence. Using these values for frequency-domain simulations is also a relatively straightforward process, and well documented in the literature.1 Transient simulation techniques for handling these frequency-dependent RLGC values, however, are actively being researched. A unique advantage of the HSPICE® circuit simulator is its implementation of an advanced technique for handling frequency-dependent RLGC matrices for coupled transmission line systems. Known as the W-element, HSPICE uses recursive convolution methods2,3 to accelerate the time-domain simulations, while still making accurate use of the frequency-domain RLGC data.
The W-element is widely used for high speed digital printed circuit board (PCB) signal integrity applications, typically in the range of 1 to 6 GHz. However, the W-element algorithm has no hard frequency limits. Its frequency range of applicability is limited only by the range of applicability of transmission line theory to the component geometry, and by the accuracy of the frequency-dependent RLGC parameters provided. Successful use of the W-element for RF and microwave frequencies is then contingent upon good extractions of the required RLGC data. The integration approach described in this article provides such a solution. Frequency-dependent RLGC data is computed accurately within the RF and microwave design software for each transmission line structure. The appropriate W-element models are then constructed for HSPICE transient simulation.
In other transient simulation tools, transmission lines are modeled with oversimplified low frequency approximations, such as an assumption of constant, frequency-independent, RLGC parameters, or by completely neglecting losses. At microwave frequencies, however, dispersion, skin effect and other frequency-dependent losses must be modeled accurately to obtain useful simulation results. The HSPICE W-element approach is based on decomposing the coupled transmission line system into several well-behaved transfer functions based on the system’s characteristic admittances and complex propagation factors. The decomposition is such that frequency dependencies can be accurately taken into account in the time domain with rational function approximations analyzed with recursive convolution. This approach has several distinct advantages over other available techniques:
- Performance is superior to that of direct numerical convolution available in competing products (linear vs. quadratic scaling of the CPU time with the length of transient simulations). After initialization, a W-element is not much more expensive in transient simulations than a resistor.
- The frequency dependence of RLGC parameters can be user-specified (in tabular format), or extrapolated based on standard skin effect and loss-tangent parameters.
- Coupled transmission lines with any number of signal conductors can be modeled.
Modal decomposition for multi-conductor lines is handled automatically.
As with any modeling approach, some caution must be exercised with the W-element to avoid possible undesirable effects:
- Transient simulations of extremely short and extremely long transmission lines should typically be avoided.
- The interdependencies of frequency-domain RLGC data should be preserved (for example, the relationship between R (f) and L (f) values due to skin-effect). This is necessary to ensure causality in the time-domain simulation.
- Correct asymptotic behavior of the RLGC data at high frequencies is needed for causality and accuracy in broadband simulations.
With careful generation of the RLGC data, and by observing the cautions noted above, the W-element provides exceptional accuracy. In the Analog Office™ environment, the RLGC model generation is performed automatically, in accordance with the described precautions. As a result, transient simulations with multiple W-elements produce errors in the calculated voltages that never exceed 0.1 per cent.

Fig. 1 A bandpass filter implemented with edge-coupled transmission lines.
The need for transient simulation is especially important for circuits containing nonlinear devices (including FETs, bipolar junction transistors (BJT) and diodes), but the accuracy of this approach is more clearly demonstrated with a simple linear example. As a typical RF/microwave design with distributed components, consider the bandpass filter based on edge-coupled transmission lines shown in Figure 1. Note that the filter schematic includes models to account for line-width discontinuities (microstrip-step (MSTEP) models and open-circuit end-effects (MOPEN) models). The Analog Office software includes sophisticated frequency-domain models for each element within the filter based on geometric and substrate parameters. These models include dispersion and frequency-dependent loss effects. From these internal models, an equivalent HSPICE W-element model is generated as a frequency-dependent RLGC data set. The quality of the Analog Office-to-HSPICE translation can be examined in the frequency-domain using scattering parameters. Figures 2 and 3 show this comparison in terms of the input reflection coefficient and insertion loss for the complete filter. Both the dB plots and Smith chart loci show excellent agreement.
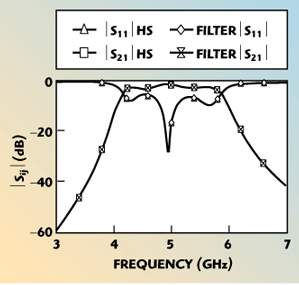
Fig. 2 Filter S-parameters calculated using models (Filter) and HSPICE (HS).

Fig. 3 S-parameters of the edge-coupled filter calculated from internal models (Filter) and HSPICE (HS).
The quality of the translation for the purposes of transient simulation can be examined through the use of Fourier analysis.4 The Fourier analysis will yield the steady-state waveforms of the circuit, while the transient simulation will follow the time-domain waveform evolution of the circuit. These two types of analyses can be compared through the appropriate choice of simulation conditions. The steady-state results calculated using Fourier analysis and the transient simulation results are suitable for comparison if:
- The transient simulation is run for a time interval sufficiently long for the transient processes in the circuit to die out, and steady state is reached;
- The period of the fundamental frequency used for Fourier analysis is much greater than the duration of the transient processes (pseudo-transient analysis using Fourier expansion).
In order to evaluate the accuracy of the transient simulations with the described approach, a classic test circuit was constructed by connecting a pulse voltage source at port 1 with an amplitude of 5 V, a rise/fall time of 0.1 ns and a pulse width of 2 ns. The filter is loaded at port 2 with a 100 W resistor. Since the test circuit is linear, Fourier analysis can evaluate the reference solution. A large fundamental period (10 ns) and a large number of harmonics (n = 4096) are used to ensure Fourier series convergence for all practical intents and purposes. Furthermore, the transient simulations were run for 80 ns (8 periods of the fundamental frequency), and only the last period was shown for comparison. The Fourier analysis was performed using the harmonic balance simulation capabilities of the design software. The pulse response comparison between the Analog Office and HSPICE models is shown in Figure 4. As before, excellent agreement was achieved, validating that this approach provides a means to realize accurate transient, time-domain simulations by translating frequency-domain models into HSPICE W-elements.

Fig. 4 Transient simulations using HSPICE compared with Fourier analysis (F=0.1 GHz).
Transient Simulation with Models Obtained from EM Analysis
At RF and microwave frequencies, numerical EM analysis is the most trusted method for characterizing many components. Often it is necessary to incorporate the results from EM analysis (typically frequency-dependent N-port S-parameters) as models for transient simulation. Methods based on fitting lumped circuits of fixed topology do not typically achieve the required accuracy (–30 to –20 dB) over a wide frequency range. In this approach, two methods are provided to incorporate the table-specified, frequency-dependent S-parameters into a transient simulation:
1. Rational function approximation of the N-port admittance matrices.
2. Direct numerical convolution.
Method 1 can be used only for passive devices and has been shown to be highly accurate and computationally efficient (note that for the purpose of this discussion passivity means that the device does not generate power, so devices such as spiral inductors, couplers, filters, transmission line discontinuities, etc., are certainly passive). The rational function approximation is performed within the Analog Office software. The method used is a combination of those described in various references, including the vector fitting (VECTFIT) method by Bjorn Gustavsen and Adam Semlyen.5,6 The method operates on N-port admittance matrices and ensures passivity of the generated model. The rational functions computed are then translated to HSPICE in the form of voltage-controlled current sources (VCCS) with Laplace transfer functions. The MNA stamps for these sources are calculated efficiently using a state-variable formulation, and no numerical convolution is necessary.

Fig. 5 HBT amplifier with spiral inductors modeled using S-parameters derived from EM analysis.
Method 2 is more general, and allows for active devices (such as S-parameters for a biased FET) and may be more tolerant of noisy data. Yet, its accuracy for distributed models is lower (in the authors’ experience) and the CPU time scales quadratically with the length of the simulated transient. Method 2 also permits simulations with non-causal models (if desired), while causality is strictly enforced with Method 1. Transient simulation with non-causal models is discouraged, since the results may not be physically meaningful.

Fig. 6 Spiral inductor used for tuning of the HBT amplifier.
An example using EM-derived data is the heterojunction bipolar transistor (HBT) amplifier with spiral inductors shown in Figures 5 and 6. The scattering parameters for the spiral inductors were computed from EM analysis, and rational function approximations (Method 1) were used to translate the EM analysis results into HSPICE models for transient simulation. A Gummel-Poon BJT model was used for the HBT device.
The transient simulation results for the HBT amplifier example are shown in Figure 7. Since large capacitors (100 pF) and inductors (100 nH) were present in the circuit, it takes on the order of 160 ns for the transient processes to finish. The rational approximation is constructed during an initialization stage that takes approximately one second of CPU time.

Fig. 7 Transient simulation of the HBT amplifier.
In order to verify that the transient simulation produces results consistent with the frequency-domain data, the transient waveforms at steady state can be compared with those computed from harmonic balance analysis. In Figure 8, the last two periods of the transient waveform are plotted with the steady-state waveform derived from HB analysis. The plots demonstrate outstanding agreement between HSPICE transient and harmonic balance simulations.

Fig. 8 Transient HSPICE simulation results at steady state compared with the waveform computed using harmonic balance.
Conclusion
This article presents a unique approach to transient simulations of microwave and RF circuits using Applied Wave Research’s (AWR) Analog Office software for high frequency design integrated with HSPICE from Synopsys. The approach is based on decomposing circuits into components that are either uniform transmission lines, or elements of reasonably small electrical length. Accurate modeling of distributed components such as interconnects, transmission lines, transmission line discontinuities (such as T-junctions, crosses, etc.) and microwave devices (such as spiral inductors and baluns) is essential if accurate simulation results for the complete circuit are to be obtained. Accurate transient simulation of transmission lines is obtained by using the HSPICE W-element with frequency-dependent RLGC matrices that are automatically generated from the internal frequency-domain component models in Analog Office software. Also demonstrated was an accurate and efficient approach to transient simulation using models for passive components based on rational function approximations of frequency-dependent N-port parameters. Especially useful for simulations based on EM-analysis results, the rational function approximations are converted to Laplace transfer function models for efficient HSPICE simulation. Extensive testing with realistic user circuits has demonstrated the success of these approaches.
HSPICE is a registered trademark of Synopsys Inc. AWR is a registered trademark and Analog Office is a trademark of Applied Wave Research Inc. All other trademarks are the property of their respective owners.
References
1. C.R. Paul, Analysis of Multi-conductor Transmission Lines, John Wiley & Sons Inc., New York, NY, 1994.
2. D.B. Kuznetsov and J.E. Schutt-Aine, “Optimal Transient Simulations of Transmission Lines,” IEEE Transactions on Circuits and Systems, Vol. 43, No. 2, February 1996, pp. 110–121.
3. K.S. (Dan) Oh, “Accurate Transient Simulation of Transmission Lines with the Skin Effect,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, Vol. 19, No. 3, March 2000, pp. 389–396.
4. S.G. Grivet-Talocia and F.G. Canovero, “TOPLine: A Delay-dole-residue Method for the Simulation of a Lossy and Dispersive Interconnect,” IEEE 11th Topical Meeting on Electrical Performance of Electronic Packaging Digest (EPEP), Monterey, CA, October 21-23, 2002, pp. 359–362.
5. B. Gustavsen, “Computer Code for Rational Approximation of Frequency-dependent Admittance Matrices,” IEEE Transactions on Power Delivery, Vol. 17, No. 3, 2002, pp. 1093–1098.
6. B. Gustavsen and A. Semlyen, “Rational Approximation of Frequency Responses by Vector Fitting,” IEEE Transactions on Power Delivery, Vol. 14, No. 3, 1999.
