Microwave filters are essential components in modern wireless communications systems. It is important to reduce their size and weight in order to integrate them with other components in a single chip system.1 A main trend in filter design is a multilayer filter, which has a much better quality than a planar one.2 At microwave frequencies, a negative permeability over a given frequency range can be realized in the magnetic resonance frequency of a periodic array of SRRs.3 In this article, a multilayer technology and an SRR structure are combined for the design of a novel multilayer filter. Compared with the conventional microstrip filter, the proposed filter shows a significant size reduction and improved selectivity. The measured and simulated results are in good agreement.
Theory
Shown in Figure 1, the SRR is made of two concentric rings separated by a gap, both having splits at opposite sides. The geometrical parameters, such as the split width, gap distance, metal width and radius are represented by d, t, w, and r, respectively. The subscripts i and o denote the inner and outer rings. Besides the electric and magnetic coupling, the incident field also induces the magnetoelectric coupling. An SRR not only has an electric resonance, but also has a magnetic resonance. In addition, the magnetic resonance frequency is lower than the electric resonance frequency.4 Using the magnetic resonance of the SRR in the filter design, a significant size reduction can be obtained.
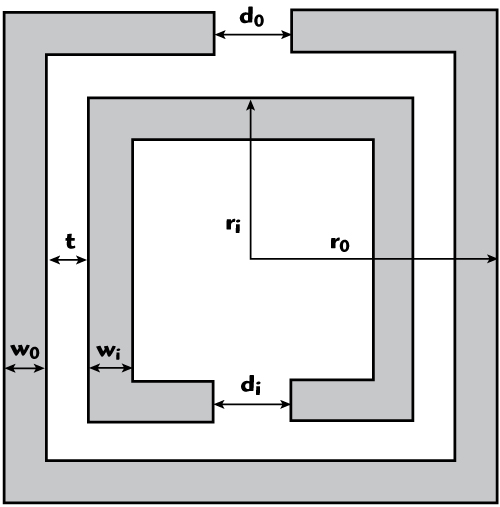
Figure 1 Split-ring resonator schematic.
The magnetic resonance of the SRR depends on its orientation with respect to the external electric field E and the direction of propagation k, which implies six distinct orientations. In the first two cases of Figure 2, in which the magnetic field penetrates through the rings, the magnetic resonance of the SRR is excited by the magnetic field. The electric field can also excite the magnetic resonance when the incident wave penetrates through the rings and the external electric field E is parallel to the split-bearing sides.5 However, when the external electric field E is rotated perpendicularly to the split-bearing sides, no magnetic response is produced, as in the two cases c and d. In the other two cases, the external electric field E penetrates through the rings. No magnetic response is produced.
Figure 2 Six orientations of the SRR with responect to k, E, H, of the incident TEM field.
To account for the magnetoelectric coupling in Maxwell’s equations, the SRR metamaterials can be described by the constitutive relations6
with 
, where 
and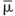 
are the relative electric permittivity and relative magnetic permeability tensors, and 
is the magnetoelectric coupling dimensionless tensor. For different axes fixed to the SRR as shown, only certain components of , 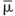and tensors are of significance.
Considering the forward plane wave propagation of the form exp (-iβz'), for case c, which will be used in the following filter design,
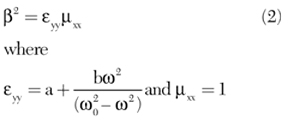
When εyy < 0, a transmission stop band occurs. Through a similar analysis, the other cases can be proved.
Design and Simulation
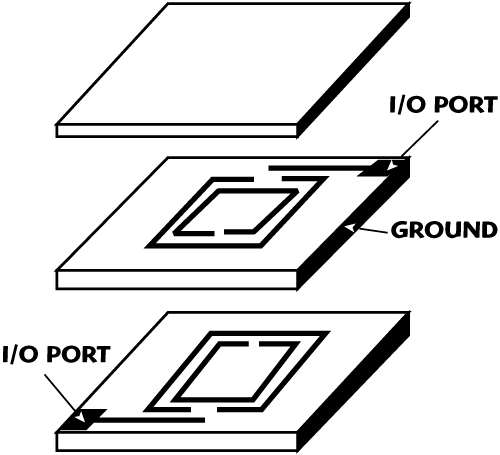
Figure 3 Structure of the two-pole SSR filter with skew-symmetric feed.
Figure 4 Photograph of the fabricated filter.
Figure 3 shows the proposed filter, which is composed of a three-layer medium with the same relative permittivity εr = 2.2 and two SRRs metal layers embedded between the medium layers in the same plane but with splits laid in opposite directions. The most important innovation here is the ground, which is located in the right and left as shown. This design makes the external electric field E parallel to the split-bearing sides and makes sure the magnetic resonance of the SRR take place, according to case c. The SRR filter with skew-symmetric input and output feed lines coupling on the first and last resonators possesses two extra transmission zeros, lying on either side of the passband, because the delays of the upper path and the lower path are the same. A photograph of the fabricated filter is shown in Figure 4. The thickness of the first and third layers is 0.8 mm and the middle layer is 2.5 mm thick. The width of the feed line is 0.2 mm. In the photographs, the left is the inner structure of the filter and the right is the whole structure.
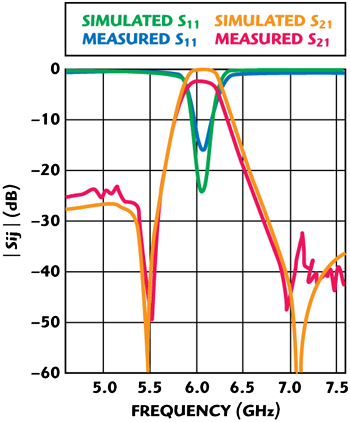
Figure 5 Simulated and measured responses of the SRR filter.
The simulated and measured results are shown in Figure 5. From the EM simulation, the filter has a fractional bandwidth of 7 percent at 6.07 GHz, an in-band return loss of 20 dB and a minimum out-band loss of 25 dB. The transmission zeros are obtained near the passband at ƒ1= 5.49 GHz and ƒ2 = 7.1 GHz. This structure offers a good transmission characteristic and a compact size, which is less than one third of the wavelength in free space. From the measured data, the two transmission zeros, 5.53 and 6.96 GHz, are found in the passband response of the filter. Good agreement can be observed between the simulated responses and measured results.
Conclusion
In this article, the relationship between the magnetic resonance of an SRR and its orientation relative to the incident wave has been analyzed. A filter using two resonators with compact size, low insertion loss and sharp-rejection has been successfully designed. Furthermore, with the skew-symmetric feed structure, transmission zeros can be achieved. Good agreement between measured and simulated data has been demonstrated.
Acknowledgment
This work was supported by the program for New Century Excellent Talents in University (NECT-04-0950).
References
1. W. Menzel, H. Schumacher, W. Schwab and X.K. Zhang, “Compact Multilayer Filter Structures for Coplanar MMICs,” IEEE Microwave and Guided Wave Letters, Vol. 2, No. 12, December 1992, 2, pp. 497-498.
2. W.S. Tung, Y.C. Chiang and J.C. Cheng, “A New Compact LTCC Bandpass Filter Using Negative Coupling,” IEEE Microwave and Wireless Components Letters, Vol. 15, No. 10, October 2005, pp. 641-643.
3. M. Shamonin, E. Shamonina, V. Kalinin and L. Solymar, “Properties of a Metamaterial Element: Analytical Solutions and Numerical Simulations for a Singly Split Double Ring,” Journal of Applied Physics, Vol. 95, No. 7, April 1, 2004, pp. 3778-3784.
4. K. Aydin, I. Buly, K. Guven, M. Kafesaki, C.M Soukoulis and E. Ozbay, “Investigation of Magnetic Resonances for Different Split-ring Resonator Parameters and Designs,” New Journal of Physics, Vol. 7, No. 168, August 2005, pp. 1-15.
5. N. Katsarakis, T. Koschny, M. Kafesaki, E.N. Economou and C.M. Soukoulis, “Electric Coupling to the Magnetic Resonance of Split Ring Resonators,” Applied Physics Letters, Vol. 84, No. 15, April 1, 2004, pp. 2943-2945.
6. C. Krowne, “Electromagnetic Theorems for Complex Anisotropic Media,” IEEE Transactions on Antennas and Propagation, Vol. 32, No. 11, November 1984, pp. 1224-1230.
