Compact frequency synthesizers fill many needs in modern communications systems. To achieve full-sized performance in miniature packages, this research work describes a line of extremely compact frequency synthesizers that leverage a novel, patented voltage-controlled oscillator technology for the stability and low noise needed for emerging wideband, high-data-rate wireless communications systems.1-8
There are two cost-effective synthesized source generation techniques: (1) the integrated IC, which consists of a PLL and an onboard VCO and (2) the VCO module with PLL circuitry added internally. While the first approach offers integrated solutions with a compromise in performance, a discrete planar VCO’s solution requires a large real estate PCB area. In addition, integrated chip solutions require an additional resonator tank or loop filter with dedicated control software.
RF system designers stress the need for higher levels of integration in RF function blocks. Such a modular approach provides amenable RF and digital interfaces, therefore speeding the time to market and simplifying system-level integration. Unfortunately, commercially available VCOs do not provide a low-cost and power-efficient solution in a compact size that addresses these needs. This article addresses the above limitations and offers a line of plug-n-play tiny VCOs with PLL, providing a high performance synthesized source that features cost-effectiveness and quick development.
VCOs provide the frequency generation in a wide range of frequency synthesizers for communications. Ideally, they deliver wide tuning ranges with low phase noise. Resonators for these oscillators can be formed in many ways, including ceramic and surface-acoustic-wave (SAW) structures. But such three-dimensional (3D) resonators do not lend themselves to integrated circuit (IC) realizations and tend to be sensitive to vibration, microphonics and phase hits. To overcome the limitations of VCOs based on 3D resonators, the planar resonators were shrunk, while also applying a unique evanescent-mode electromagnetic (EM) coupling mechanism to improve the loaded quality factor (Q) of the coupled planar resonators and thus reduce the phase noise. The result is a line of patent-pending, compact, coupled-planar-resonator VCOs that fit in packages measuring just 0.3" X 0.3", but can match the phase noise performance of much larger, high-Q resonator-based oscillators. Because of their (low mass) printed coupled resonators, they are immune to high levels of shock and vibration, a major advantage over oscillators using crystal, ceramic, SAW and YIG resonators. The tiny VCOs are RoHS compliant and can be supplied in tape-and-reel format for automated assembly. They have been tested through 12 GHz and are in production. The innovative, low-power, low-phase noise oscillator technology is currently available in discrete-component form, but is ready to make a transition to integrated circuits. In addition, the planar resonator approach readily lends itself to semiconductor processing methods for fabrication of integrated-circuit reference oscillators using CMOS/BiCMOS/SiGe/GaAs technologies.
Theory and Requirements
Frequency synthesizers come in many shapes and sizes, from tiny system-on-a-chip (SoC) devices and compact modules to rugged military-grade rack-mount systems and bench-top instruments. Available technologies are almost as diverse as the number of package options, using analog methods, digital techniques and often a combination of the two. Frequency synthesizers have traditionally relied on a phase-locked loop architecture in which the phase of a tunable oscillator, such as a VCO or YIG-tuned oscillator, is locked to the phase of a reference source with higher stability, such as an oven-controlled crystal oscillator (OCXO).
Basic Requirements
Bandwidth and Frequency Coverage
Bandwidth is vital to the spread of wireless multimedia, instant data, high voice quality and other key services.26-28 However, it is also a limited resource, requiring the use of advanced amplitude- and phase-based modulation formats to squeeze the maximum amount of information into a given portion of bandwidth. One of the most critical components in enabling maximum bandwidth efficiency is the microwave frequency synthesizer. Modern synthesizers leverage available digital techniques to reach the level of noise, stability and resolution needed for most modern communication systems. Therefore, it may be advantageous to develop a broadband “generic” but low cost and power-efficient solution that can cover a number of applications.26
Spurs and RF Output Power
Spurs are undesired artifact products generated by synthesizers at discrete frequencies and their location and level are determined by synthesizer architecture and frequency plan. Care must be taken to minimize the spurs’ levels down to -80 dBc and below. The RF output power level is another key factor that drives the frequency conversion (up- and down-conversion) mechanism in mixer circuits and can range over wide limits, typically -10 to +18 dBm, although some applications may need even more power.26
Phase Noise and Switching Speed
Phase noise is the prime parameter that limits the sensitivity of receivers. Synthesizer close-in phase noise and stability depend on the reference frequency standard and synthesizer topology, which derives its output from the reference. Switching speed (tuning speed) is a demanding parameter for data processing, which determines how fast the synthesizer response jumps from one desired frequency to another. The major challenge a designer faces is increasing the switching speed (<< milliseconds) of the synthesizer without sacrificing the performance (phase noise and spurious) as dictated by ongoing increasing data rates of current and later generation communication systems.
Size and Power Consumption
Compact size and low power consumption are key criteria for modern synthesizer technology. Therefore, they are a true motivation towards integrated circuits, avoiding costly, bulky and power hungry YIG-tuned synthesizers. System designers feel persistent pressure to deliver high performance synthesizers in compact size with low power-consumption, including inexpensive solutions. The above limitations (tuning speeds, power consumptions, phase noise, spurious, stability and size) present design challenges and tradeoffs and are likely to be the key driving factors towards overcoming these as well as reducing complexity and cost.26-29
Synthesizer Architectures
Frequency synthesizers provide the fixed and tunable signals for local oscillators in a wide range of commercial and military communications systems, including wireless base stations. Technologies for creating frequency synthesizers are diverse, from traditional analog methods using PLLs to direct digital synthesizers (DDS) that rely on high-speed digital-to-analog converters (DAC) to transform digital input words into analog output signals.27 While reviewing classical synthesizer architecture, the current technology trend toward increasing the flexibility and functional integration is specifically addressed as well as reducing its complexity and cost without compromising the phase noise performance and switching speed. Various synthesizer architectures along with their main characteristics are described below.26
Direct Analog Synthesizers (DAS)
The function of a synthesizer is translating one or more reference signals to a number of output frequencies with a desired step size. Direct analog synthesizers are conceptualized by mixing base frequencies, followed by switched filters, as shown in Figure 1. The base frequencies can be obtained from a low frequency high performance signal source (crystal and SAW resonator-based oscillators) or high frequency spectral pure signal source (Dielectric Resonator, Bulk Acoustic Wave Resonator, Sapphire Resonator, Metal Cavity Resonator and Coaxial Resonator-based oscillators) by frequency multiplication, division, phase locking or injection-mode locking. The advantage of DAS is low phase noise (due to high performance base frequency sources extracted from high Q-factor resonator-based oscillators: (crystal/SAW/SRO/CRO) and fast switching speed, but at the cost of step size, design complexity and overall component counts (base frequency source, mixer and filter circuits).

Figure 1 Typical block diagram of a DAS.
The alternative solution is to incorporate a DDS module at the input of the DAS to increase the minimum step size required from the direct analog approach, as shown in Figure 2. Again the drawback of this approach is a large amount of undesired mixing products, which can be filtered out with expensive filtering hardware structures if small frequency step size and wide coverage are needed.

Figure 2 Typical block diagram of a DAS using DDS at the input.
Although DAS techniques are a promising solution for reasonably good switching speed and phase noise performance, their applications are limited due to high cost factor.
Direct Digital Synthesizers (DDS)
In contrast to traditional concepts, DDS offers exceptionally fine resolution sub-hertz level, but at the cost of limited usable bandwidth and spurious performances. Therefore, due to bandwidth and spurs limitations DDS techniques are not attractive for microwave applications and are generally used as a fine frequency resolution module in direct analog or indirect architecture. The above limitations can be overcome by incorporating software and hardware techniques similar to the DAS approach (large number of component counts), followed by a frequency divider, as shown in Figure 3.

Figure 3 Typical block diagram of a DDS using a divider at the output.
Indirect Frequency Synthesizers (IFS)
Figure 4 shows a typical single-loop IFS, which utilizes frequency conversion (mixing) in the feedback path to improve the switching speed, phase noise and spurious performances. The drawback of a conventional IFS is degradation in the phase noise performance, due to the large division ration N, which is required to provide a high frequency output with a fine resolution. In addition, IFS is sensitive to false lock due to undesired mixing products. Using a fractional divider, the overall loop division ratio can be reduced for improved phase noise and tuning speed characteristics.

Figure 4 Typical block diagram of an IFS.
The problem of false locking can be overcome by incorporating a digital to analog converter (DAC) to provide a sufficiently accurate coarse tune of the VCO to a reasonably correct frequency. This acquisition aid needs linear and repeatable tuning characteristics over the operating frequency band and temperature range. But DACs are noisy and adversely affect the synthesizer phase noise performance if they are not properly removed after the initial frequency acquisition.29
For a given step size, fractional-N schemes enable a higher phase detector (PD) comparison frequency, resulting in improved phase noise and tuning speed characteristics. However, the main drawback of the fractional-N topology is high spurious levels due to phase errors inherent to the fractional division mechanism.
IFS architecture strongly depends on the VCO characteristics; therefore, a promising solution is to use a low phase noise and fast switching compatible VCO, including a DDS module as a fractional divider, inserted into the reference or divider path (see Figure 5). This approach leads to a complex hardware architecture, but offers a cost-effective high performance solution. Although high performance synthesizer compatible VCO solutions complicate the overall design philosophy, the complexity can be effectively spread and optimized, which leads to a high performance and reasonably priced frequency generation and synthesis solutions for current and later generation communication systems.

Figure 5 Typical block diagrams of a fractional-N synthesizer with DDS inserted.
Synthesizer Compatible VCOs
Historically, synthesizer designers have relied on YIG oscillators, characterizing broadband operation with excellent phase noise performance. The YIG oscillator offers linear tuning characteristics that simplify the synthesizer coarse-tuning algorithm in multi-loop schemes. These unique features allowed the YIG-based synthesizers to dominate over the last decades. But YIG oscillators are power hungry and require larger real estate area, which recently contributed to a transition to printed coupled resonator-based solid-state VCO architectures. Since the printed resonator-based VCO noise performance is inferior to its YIG counterpart, care must be taken in choosing spectral pure reference frequency sources (crystal oscillators). The typical phase noise performance of commercially available 100 MHz crystal oscillators is -168 dBc/Hz at 10 kHz offset from the carrier.25 The phase noise at 10 kHz offset for a 100 MHz crystal oscillator can be translated to -128 dBc/Hz for a 10 GHz output, which even supersedes the performance of commercially available low cost YIG oscillators (assuming the translation is not affected by the synthesizer system noise floor). As shown in Figure 6, this work addresses the noise minimization mechanism for a 155 MHz reference frequency standard, using a patented active-mode-feedback and noise filtering techniques.1-8 Figure 7 shows the typical measured phase noise plot at 10 kHz offset, which is better than the commercially available low cost frequency standard. At a lower offset (1 Hz), the improvement in phase noise performance is limited due to the influence of the 1/f noise, which can be optimized by selecting a transistor that has low value of 1/f noise.
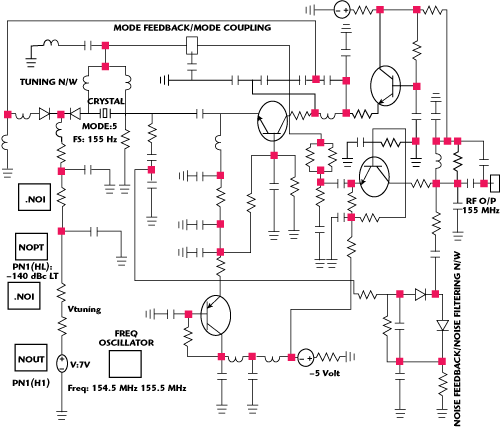
Figure 6 155.6 MHz active-mode coupled VCXO (0.5" X 0.5").

Figure 7 Measured phase noise for a 155.6 MHz VCXO.
Tunable oscillators are instrumental in the operation of many systems, from commercial communications to military radars. Many characteristics define the performance of a tunable RF/microwave oscillator, but one of the more difficult parameters to optimize is phase noise. Because of the importance of bandwidth and phase noise in modern systems, this research work is focused on those two parameters in their innovative line of compact coupled planar resonator (CCPR) oscillators. Figure 8 shows the typical layout of a reference frequency standard using evanescent node and extended resonance techniques in CCPR configuration. Figure 9 shows the measured phase noise plots for different carrier frequency. At 10 kHz offset from the carrier, the typical values are: -138 dBc/Hz (carrier frequency: 622 MHz), -128 dBc/Hz (carrier frequency: 2488 MHz) and -118 dBc/Hz (carrier frequency: 4200 MHz). The circuit operates at 5 V, 30 mA and its typical output power is 5 dBm. The second harmonic rejection is better than -20 dBc. Figure 10 shows the measured phase noise plot for a 999.96 MHz spectral pure VCO using hybrid techniques (combination of planar resonator and inexpensive low Q SAW resonator). The typical measured phase noise at 10 kHz offset is -142 dBc/Hz, which is state-of-the-art technology in low-cost series of reference frequency standards in planar technology.
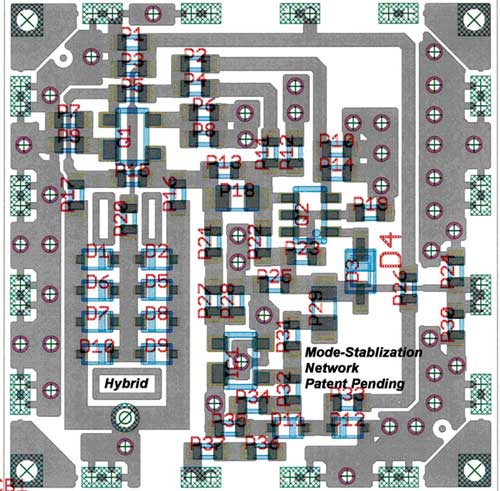
Figure 8 Typical layout of a 1000 MHz low noise oscillator (0.5" X 0.5").

Figure 9 Measured phase noise for a CCPR VCO.

Figure 10 Measured phase noise for a 1000 MHz oscillator.
The above discussions on reference frequency standards call for wideband VCO solutions; the results are evident. The printed resonator VCO described in this article potentially achieves faster tuning speed with comparable phase noise and spurious performance without the use of expensive, bulky and power hungry YIG oscillators. Recent progress is in the direction of minimizing the system residual noise floor and extending the loop bandwidth to a few megahertz, where printed coupled resonator-based solid-state VCO noise becomes competitive with the YIG oscillators. Incorporating a high performance planar resonator-based VCO with a crystal oscillator as a reference results in a cost-effective synthesizer with faster tuning speed. Besides choosing the right VCO, the PLL bandwidth is one of the most important design parameters. If the noise in the input or feedback path is dominant, the bandwidth should be small to filter it out by the PLL loop. If the VCO noise is dominant, the bandwidth should be large, since this noise is high-pass filtered to the PLL output.
These characteristics, accompanied with the low cost inherent to printed coupled resonator-based VCO designs, are likely to secure their domination in the foreseeable future. VCOs based on IC technology can be made small, but at the cost of power consumption and limited tuning range. This work describes the power-efficient fundamental frequency VCO solution that supports as much as 2:1 bandwidths from 1 to 12 GHz, with fast tuning and low phase noise performance that challenge the best performance of commercially available integrated circuit or discrete SMD packaged VCOs (for given constraints of power consumption, tuning, performance and cost factor).
Figures 11 and 12 show the block diagram and layout for the DCO/DXO VCOs. It is the miniature size of the discrete-device DCO and DXO series VCOs that make the surface-mount MFSH series synthesizers possible. They can be used with supply voltages of 2.1, 3.0, 3.2, 3.5, 4.0, 4.5, 5.0, 8.0 and 12 V, with supply current as low as 10 mA, without much degradation in phase noise performance and characteristics. VCO models are available for narrowband tuning (approximately 10 percent of center frequency), moderate bandwidth (approximately 50 percent of center frequency) and wideband tuning (greater than 100 percent of center frequency). The tiny VCOs are suitable for use as free-running sources as well as for space-saving synthesizer designs. They are designed for reliable performance over temperatures from -40° to +85°C and are well suited for applications in industrial, military and commercial systems. They employ a miniaturized, multi-coupled, stubs-tuned-planar-resonator (MCSTPR) approach, fabricated on low-loss 30 mil-thick dielectric material with a dielectric constant of 3.38. The VCO’s active device is a discrete low-noise silicon-germanium (SiGe) hetero-junction bipolar-transistor (HBT) device.

Figure 11 Block diagram of a miniaturized VCO.

Figure 12 Layout of the miniaturized VCO (0.3" X 0.3" X 0.1").
The MCSTPR structure is modeled using a 2.5D or 3D EM simulator and incorporated into an optimized nonlinear oscillator circuit to achieve configurability and low-phase noise operation over the desired frequency band. The nonlinear circuit model contains the oscillator’s active device, represented by its S-parameters. This partitioning of the oscillator into its modeled component parts works quite well, and the combination of the S-parameters and the nonlinear circuit model agrees closely with measured data from circuits already constructed. The active device SiGe HBT is represented by large-signal S-parameters in order to better understand the behavior of the device under quasi-linear (low-signal drive level) and nonlinear (large-signal drive level) conditions. This approach improves the optimization cycles using harmonic-balance simulators such as Advanced Design System (ADS 2008) from Agilent Technologies and Ansoft/Nexxim/Ansys from Ansoft Corp. to limits allowed by physics.
Printed Coupled Resonators

Figure 13 Typical simplified structure of open loop microstrip coupled resonator networks.
The Q (quality) factor of the coupled planar resonator network can be enhanced by introducing an optimum coupling mechanism (electric/magnetic/hybrid). Figure 13 illustrates the layout of the typical electric, magnetic, hybrid-coupling planar resonator networks, and oscillator circuits for comparative analysis.24 As described, the coupling dynamics can be characterized by proximity effect through the fringing fields, which exponentially decay outside the region; the electric and magnetic field intensities tend to concentrate near the side having maximum field distribution. The coupling factor β (βe: electric, βm: magnetic and βh: hybrid) can be described as

The loaded quality factor QL of the coupled resonator network is given in terms of unloaded quality factor Qo as24

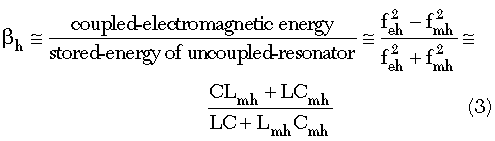
where
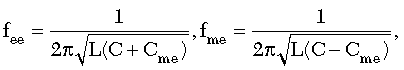
Cme: Mutual Capacitance

Lmm: Mutual Inductance

Lmh: Hybrid Inductance
 f0: Fundamental resonance frequency of uncoupled resonator. (4)
f0: Fundamental resonance frequency of uncoupled resonator. (4)
The loaded quality factor QL of the coupled resonator network is given in terms of unloaded quality factor Qo as24




where  is the rate of change of the phase, and Q0 is the unloaded Q-factor of the uncoupled single open loop microstrip line resonator.
is the rate of change of the phase, and Q0 is the unloaded Q-factor of the uncoupled single open loop microstrip line resonator.
From Equations 6, 7 and 8, there is trade-off between improving the Q factor and the permissible attenuation required (which is compensated by active device for oscillation build up). The coupling mechanism described shows improvement in quality factor in comparison to a single uncoupled planar resonator, but the drawback is a limited tuning range (less than 1 percent).
From Equations 6, 7 and 8, the loaded quality factor (QL) can be maximized by either lowering the value of mutual capacitance (Cm) and inductance (Lm) or maximizing the self-capacitance (C) and inductance (L). Therefore, the upper limit of the loaded Q-factor is dependent on the coupling β that can be optimized by controlling the width of the transmission line (w), the gap of the open line resonator (p) and the spacing between the two open line resonators (d). However, dynamically controlling and tuning the parameters w, p, and d at high frequency in IC technology is a challenging task. For wideband tunability, the coupling factor βj has to be dynamically tuned for low phase noise performances over the operating frequency band. The simplified approach for the realization of a dynamically controlled coupling factor βj can be achieved by incorporating a tuning diode as a coupling capacitor across the coupled resonator networks.
VCOs Phase Noise Analysis
The expression for the phase noise can be given by11


where £(ƒm), ƒm, ƒ0, ƒc, QL, Q0, F, k, T, Po, R, m and K0 are the ratio of the sideband power in a 1 Hz bandwidth at fm to total power in dB, the offset frequency, the flicker corner frequency, the loaded Q, the unloaded Q, the noise factor, the Boltzman’s constant, the temperature in ºK, the average output power, the equivalent noise resistance of the tuning diode, the ratio of the loaded and unloaded quality factors and the voltage gain. From Equations 6, 7 and 8, m is given in terms of coupling coefficient as

By differentiating Equation 10 with respect to m and equating to zero, the local minimum value of the phase noise for a given resonator and oscillator topology can be given by

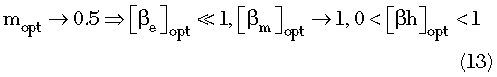
From Equation 13, for low phase noise applications, mopt and βopt should be dynamically tuned and must converge in the vicinity of mopt≅0.5 and 0<βopt<1 respectively for best phase noise performances. As an example for validation, Figure 14 shows the typical layout of a fixed frequency 12 GHz mode-coupled (MC) VCO, using a SiGe heterojunction bipolar transistor (HBT), fabricated on a Rogers substrate material with a dielectric constant of 3.38 and a thickness of 30 mils (microstripline/stripline) for the validation of the new approach (dynamically controlling mopt and βopt for minimum noise figure). Figure 15 shows the CAD simulated phase noise plot for a 12 GHz MC VCO at a 10 kHz offset from the carrier with respect to mopt and βopt. Figure 16 shows the measured phase noise plot of the discrete version of the MC VCO (which is planar and amenable to a MMIC manufacturing process), typically –110 dBc/Hz at 10 kHz from the carrier that agrees with the simulated results within 3 to 4 dB.

Figure 14 Typical layout of a 12 GHz MC VCO active planar coupled resonator (APCR).

Figure 15 Simulated phase noise of an MC VCO with respect to Mopt.

Figure 16 Measured phase noise of an MC VCO.
Applications: Tiny VCOs Arm Frequency Configurable Synthesizers
Technologies for creating frequency synthesizers are diverse, from traditional analog methods using PLLs to direct digital synthesizers (DDS) that rely on high-speed digital-to-analog converters (DAC) to transform digital input words into analog output signals. Frequency synthesizers can be categorized into mainly three groups: analogue, digital or mixed signal (hybrid). The frequency synthesizer described in this article falls into the hybrid category. The block diagram for a typical MFSH frequency synthesizer (see Figure 17) includes a VCO, PLL, IC, charge pump, loop filter, amplifier and voltage regulator.

Figure 17 Block diagram of a configurable synthesizer (MFSH series).
Conclusion
System designers stress the need for higher levels of integration in RF function blocks. Such modules provide simple digital and RF interfaces and, thus, speed the time to market and simplify system-level integration and production. Unfortunately, the RF/microwave signal sources currently available do not provide a satisfactory solution that addresses these needs. Fortunately, a line of pick-n-place tiny power-efficient VCOs offer a practical solution, providing a high performance frequency synthesized source that features quick development.
References
- U.L. Rohde and A.K. Poddar, “Wideband Voltage-controlled Oscillators Employing Evanescent Mode Coupled Resonators,” United States Patent No. 71803812, February 2007.
- U.L. Rohde, A.K. Poddar and R. Rebel, “Integrated Low Noise Microwave Wideband Push-push VCO,” United States Patent No. 7088189, August 2006.
- U.L. Rohde and A.K. Poddar, “User-definable Thermal Drift Voltage-controlled Oscillator,” United States Patent No. 7265642 B2, September 4, 2007.
- U.L. Rohde and A.K. Poddar, “Low Thermal Drift Tunable Frequency VCO,” United States Patent No. 7, 262670B2, August 28, 2007.
- U.L. Rohde and A.K. Poddar, “Feedback and Mode-coupling Improves the Phase Noise Performances of Crystal Oscillators,” 2008 IEEE International Frequency Control Symposium Digest, pp. 554-561.
- U.L. Rohde and A.K. Poddar, “Tunable Frequency, Low Phase Noise and Low Thermal Drift Oscillator,” United States Patent No. 7196591, 2007.
- U.L. Rohde and A.K. Poddar, “Multi-octave Band Tunable Coupled-resonator Oscillator,” United States Patent No. 292113, November 6, 2007.
- U.L. Rohde and A.K. Poddar, “Low Noise, Hybrid Tuned Wideband VCO,” United States Patent No. 7365612B2, April 29, 2008.
- U.L. Rohde and A.K. Poddar, “Mode-coupled VCO Replaces Expensive DRO (Dielectric Resonator Oscillator),” 2008 IEEE International Frequency Control Symposium.
- U.L. Rohde and A.K. Poddar, “Dynamic Noise Feedback and Mode-coupling Mechanism Silences the VCXO’s Phase Noise,” 2008 IEEE Radio and Wireless Symposium Digest, pp. 9-12.
- U.L. Rohde, A.K. Poddar and G. Boeck, Modern Microwave Oscillators for Wireless Applications: Theory and Optimization, John Wiley & Sons Inc., New York, NY, 2005.
- U.L. Rohde and A.K. Poddar, “Noise Minimization Techniques for RF & MW Signal Sources (Oscillators/VCOs),” Microwave Journal, Vol. 50, No. 9, September 2007, pp. 136-162.
- P.S. (Paul) Khanna, “Microwave Oscillators: The State of the Technology,” Microwave Journal, Vol. 49, No. 4, April 2006, pp. 22-42.
- J. Everard and K. Theodoropoulos, “Ultra-low Phase Noise Ceramic-based Dielectric Resonator Oscillators,” 2006 IEEE International Frequency Control Symposium Digest, pp. 869-874.
- V. Walkar and I.C. Hunter, “Design of Triple mode TE01 Resonator Transmission Filters,” IEEE Microwave and Wireless Components Letters, Vol. 12, No. 6, June 2002, pp. 215-217.
- U.L. Rohde and A.K. Poddar, “Low Cost Signal Source for Multi-band Multi-mode Wireless Systems,” Microwave Journal, Vol. 50, No. 7, July 2007, pp. 54-78.
- S. Kim, W. Wu, J. Lin, A. Verma, S. Jang, F. Ren, S. Pearton and J. Gillespie, “A High-efficiency GaN/AlGaN HEMT Oscillator Operating at L-band,” Proceedings of the 2006 Asia Pacific Microwave Conference, Yokohama, Japan.
- S. Romisch and R. Lutwak, “Low-power, 4.6 GHz, Stable Oscillator for CSAC,” 2006 IEEE International Frequency Control Symposium Digest, pp. 448-451.
- S. Hamano, K. Kawakami, and T. Takagi, “A Low Phase Noise 19 GHz Band VCO Using Two Different Frequency Resonators,” 2003 IEEE MTT-S International Microwave Symposium Digest, pp. 2189-2192.
- A.V. Grebennikov, RF and Microwave Transistor Oscillator Design, John Wiley & Sons Ltd., London, England, 2007.
- J.K.A. Everard and C. Broomfield, “Reduced Transposed Flicker Noise in Microwave Oscillators Using GaAs-based Feedforward Amplifiers,” IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, Vol. 54, No. 6, June 2007, pp. 1108-1117.
- J.K.A. Everard and L. Zhou. “Nonlinear Effects in Varactor Tuned Resonators,” IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, Vol. 53, No. 5, May 2006, pp. 853-861.
- P.A. Dallas and J.K.A. Everard, “Characterization of Flicker Noise in GaAs MESFETs for Oscillator Applications” IEEE Transactions on Microwave Theory and Techniques, Vol. 48, No. 2, February 2000, pp. 245-257.
- U.L. Rohde and A.K. Poddar, “Self-injection Locked Compact Coupled Planar Resonator-based Cost-effective Ultra Low Phase Noise VCOs for Wireless Systems,” 2007 European Conference on Circuit Theory and Design.
- U.L. Rohde and A.K. Poddar, “Voltage-controlled Crystal Oscillator,” 2009 IEEE Sarnoff Symposium, Princeton, NJ.
- A. Chenakin, “Frequency Synthesis: Current Solutions and New Trends,” Microwave Journal, Vol. 50, No. 5, May 2007, pp. 256-266.
- J. Browne, “Frequency Synthesizers Tune Communication Systems,” Microwaves & RF, March 2006.
- U.L. Rohde, Microwave and Wireless Synthesizers: Theory and Design, John Wiley & Sons Inc., Hoboken, NJ, 1997.
- W. Egan, Frequency Synthesis by Phase Lock, John Wiley & Sons Inc., Hoboken, NJ, 2000.
