A classical design approach for receivers operating at microwave frequencies is to down-convert the detected signal to some intermediate frequency before digitizing the signal. The final design of a receiver is chosen depending on performances, which can be described by various parameters. The most important ones are the broadband noise power, the close-in noise power, nonlinearity, a spurious free dynamic range, temperature stability, isolation between channels (for multiple channels systems), power consumption and price. The main parameter this article will be investigating is the close-in phase noise of the receiver’s input section.
The measurements of residual phase noise, up to 100 kHz away from the 1.3 GHz carrier, are of most interest. Figure 1 shows a simplified prototype of the receiver’s input section that has been constructed for applications in high-energy physics for the control of electromagnetic fields in superconducting RF cavities.1 For this particular application, the demands for phase stability are approximately 0.01° of the integrated RMS phase noise. The main noise contributors are identified first.
Mixer and Amplifier Noise

The following is a short overview of microwave mixer and amplifier noise. The reader should refer to the literature listed at the end of the article for more detailed reading. According to Maas,2 there are three types of noise generated in a mixer: Shot noise, thermal noise and flicker noise. Shot noise is caused by carriers passing through the junction of a PN diode. Thermal noise is caused by the series resistance in the mixer.3,4 Flicker noise is related to surface-state density of the material and is not an issue at higher frequencies.5 There are various parameters that define mixer noise performance and can be set by the designer. Among the most important are the LO power and the VSWR of the mixer ports.
The LO power has no effect on thermal noise, since the series impedance does not change with power. On the other hand, in most mixers, shot noise changes with LO power and is correlated over the whole band. This means that there will be a certain increase in the noise floor due to the mixing of these coherent components. This increase in noise floor can be avoided if proper filtering is used. The noise figure of a mixer decreases with an increase in LO to a certain point.2
The noise figure of a mixer also depends on matching.2,6,7 Using the wave representation of noise (as carried out by Penfield),8 it can be shown that the noise figure is a function of the reflection coefficient. An obvious approach to solve this problem is to have the mixer ports properly matched. Mixer matching can be achieved by using amplifiers, circulators or passive matching.6,9
The output signal-to-noise ratio of a mixer also depends on the sensitivity of the mixer. The sensitivity, or the mixer slope, defines the output DC voltage in volts at the IF port per one radian of change in phase between the RF and LO ports. It is shown in the literature6 how the mixer sensitivity changes with LO power and matching at the IF port. In general, a capacitive load on the IF improves mixer sensitivity. However, this also causes a decrease in IF bandwidth.
The other source of noise in the input section of the receiver is the microwave amplifier. It was decided to use the amplifier on the LO port since mixers usually demand relatively high LO power for linear and low noise operation. A detailed study of close-in noise added by a microwave amplifier has been presented.10 Besides broadband noise, amplifiers exhibit close-in flicker noise, which is usually not given in the manufacturer’s datasheet. This close-in phase noise generated by the amplifier is up-converted to the LO carrier that is being amplified, which is then transmitted to the IF port through the mixing process. The level of flicker noise close to the carrier that is generated by the amplifier depends on the input power to the amplifier. A more linear amplifier will decrease flicker noise.10
Measuring Method
The method that was used in this article to measure the residual phase noise has been described in various textbooks and studied in various articles.4,6 Figure 2 shows a block diagram of the measurement setup.
The low noise RF signal is first split into two branches. One of the branches is delayed by 90° and the two signals are mixed with a mixer. The low noise amplifier on the IF port of the mixer increases the dynamic range of the measuring method. The output is measured with an oscilloscope or a spectrum analyzer. In formal representation, the mixing process is described by
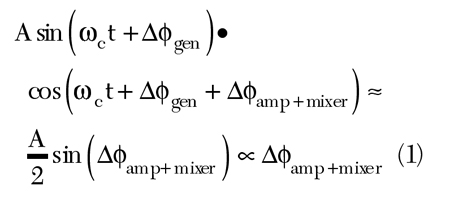
where
ωc = frequency of the carrier
Δφgen = phase noise added by the signal generator
A = product of both amplitudes
Δφamp+mixer = residual phase noise added by the input section of the receiver, that is, by the amplifier and mixer
The term representing the second harmonic is canceled out, since the phase noise is observed at base band. Small angles approximation is also assumed to obtain the expression on the RHS of Equation 1. The amplitude noise that could be included in Equation 1 as an additional amplitude modulation term is neglected since the mixer is driven close to saturation. In order to correctly translate the phase deviation into an equivalent amplitude deviation, the sensitivity (slope) of the mixer has to be measured. One of the possible ways to measure the slope is by applying slightly different frequencies (by approximately 100 kHz) on the RF and LO ports of the mixer. With an oscilloscope, one can measure a change in voltage over a time (phase) interval. The observed time interval has to be small (for instance 1/100) compared to the period of the signal for accurate slope measurements. As shown by Walls,6 the mixer sensitivity is a function of frequency. For accurate measurements, it is therefore necessary to repeat the slope measurement for each offset frequency.
When measuring phase noise with the setup shown, it is important to reduce the amplitude noise as much as possible. Filtering and driving a balanced mixer in saturation will help to reduce the amplitude noise power. It is also important to have a good match on all the ports of the mixer, which can be achieved with isolators. At the same time this guarantees better isolation between splitter ports. Last but not least, the cables of the measurement setup should be kept as short as possible.

As a measurement method check, the close-in phase noise of the signal source was measured at 1.3 GHz. The measured values over a 10 MHz bandwidth are given in Figure 3. The generator noise in dBc/Hz is compared to the manufacturer’s values and to the specified phase noise values of the dielectric resonator oscillator (DRO).14 The DRO was used to measure the generator noise using the phase noise analyzer from Wenzel Associates Inc.15 The measurements show that, due to the measuring method, the noise of the generator is subtracted out. Consequently, a lower noise floor than the one shown in the figure is measured.
Measurement Results

Using the measuring technique described in the previous section, measurements using 7, 13, 10 and 17 dBm level mixers were carried out. The MMIC amplifier (HMC481 from Hittite)11 in the LO branch was the same in all cases (except for the measurement with the active mixer). By varying the attenuation at the output of the amplifier, various power levels were achieved that were needed for each particular mixer.
Figure 4 shows the relative noise floor of phase noise measurement results in dBc/Hz. In addition to passive mixers manufactured by Mini Circuits,12 one active mixer from Hittite13 was also measured. As mentioned at the beginning of this article, the measured close-in phase noise is supposed to be generated in both the LO amplifier and the mixer. In order to check which of the two is adding more noise, the amplifier was moved in front of the splitter. In this way, the phase perturbation of the amplifier is canceled out by the measuring method. The results of this test are shown in the figure.

It is obvious that the majority of the noise is introduced by the amplifier. Measurements of various mixers, in the same configuration, show that different passive mixers with the same LO amplifier port exhibit the same flicker noise performance. This is more proof that the measured noise is dominated by the LO amplifier contribution. The green curve shows the noise floor of the active mixer.13 Although the test setup is kept the same (except for the LO amplifier), the active mixer exhibits higher phase noise over the band from 100 Hz to 10 kHz.
The RMS jitter is an often-used measure of the close-in phase noise. It is equal to the integral of twice the values measured (the measured values are SSB) over the bandwidth of interest. Table 1 summarizes the integrated RMS phase/time perturbation for some of the measured configurations. The integrated bandwidth is from 100 Hz to 100 kHz.
Nonlinearity Measurements of Mixers

In the present applications, the mixer is the input device to the receiver. According to the measurement results, the best choice for the input mixer would be a level 7 mixer since it needs the lowest LO power. However, other issues like linearity have to be considered. As mentioned previously, the LO power defines the linearity of the mixer. As a matter of fact, it is expected for a low level mixer to have poor linearity performance.
Measurements show that in practice there are exceptions to this rule. Figures 5, 6 and 7 show linearity measurements for various commercially available mixers. It is interesting to note, for instance, that the level 13 mixer starts compressing at lower input power than the level 10 mixer.
Measurements of the second and third harmonics give a more detailed insight into the linearity issues of various mixers. For example, measurements show that the second harmonic of the level 10 mixer can be compared at certain operating points to the linearity of a level 17 mixer. On the other hand, the third harmonic of the level 10 mixer is much higher than the third harmonic generated by a level 7 mixer at specific input power values. It is worth noting that the curves presented depend on LO power. It is therefore necessary for the designer to carry out extensive measurements before choosing a mixer and setting the operating point.

Conclusion
The residual phase noise introduced by a generic receiver’s front-end was measured. Different commercially available mixers were used for the down-conversion. The measurements show that the major contributor to the close-in phase noise of the simplified input stage is the LO amplifier.
From the close-in phase noise point of view, it is sometimes better to use a passive mixer with an external LO amplifier rather than an active mixer with an integrated LO amplifier. In the circumstances presented in this article, the mixer type has no effect on the relative noise floor measurements. As a consequence, the most appropriate mixer for a specific system should be chosen according to other parameters. In this article, linearity was investigated.

As expected, measurements show that, as an average, level 17 mixers along with the active mixer exhibit the best linearity performance. However, at some working points a level 13 or even a level 10 mixer can produce lower second or third harmonics than a level 17 mixer. Depending on the design, the linearity and close-in phase noise characteristics of the receiver’s front-end can be optimized by choosing the most appropriate mixer and amplifier. As an example, the requirements for a phase perturbation of 0.01° RMS and an RF port input power of +9 dBm were set. For this particular application, a mixer similar to HMC483MS8G cannot be used. According to the measurements shown, the SYM-25DLHM would be a good choice.
Acknowledgments
The authors would like to thank Frank Ludwig and Stefan Simrock of Deutsches Elektronen Synchrotron (DESY) and Archita Hati of the National Institute of Standards and Technology for their valuable and helpful comments.
References
1. U. Mavric and B. Chase, “Analog Receiver and Transmitter Design for the ILC Main LINAC LLRF Control System,” 2007 IEEE Eurocon, Warsaw, Poland.
2. S.A. Maas, Microwave Mixers, Second Edition, Artech House Inc., Norwood, MA, 1993.
3. M.W. Muterspaugh, et al., “Single Balanced Mixer Output Filter,” US Patent 5,034,994, July 1991.
4. F.L. Walls, et al., “Extending the Range and Accuracy of Phase Noise Measurements,” Proceedings of the 42nd Annual Symposium on Frequency Control, 1998, pp. 432–441.
5. B.C. Henderson, “Mixers in Microwave Systems: Part 1,” Watkins-Johnson Co. Tech-Notes, Vol. 17, No. 1, January 1990.
6. F.L. Walls, et al., “Accurate Measurements of Spectral Density of Phase Noise in Devices,” Proceedings of the 31st Annual Symposium on Frequency Control, 1977, pp. 335–343.
7. P. Will, “Reactive Loads: The Big Mixer Menace,” Microwave, April 1971, pp. 38–42.
8. P. Penfield, “Wave Representation of Amplifier Noise,” IRE Transactions on Circuit Theory, Vol. 9, No. 1, March 1962, pp. 84–86.
9. “Doubly-balanced Mixer Termination,” US Patent 4,601,063, July 1986.
10. A. Hati, et al., “Merits of PM Noise Measurements Over Noise Figure: A Study at Microwave Frequencies,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 53, No. 10, October 2006, pp. 1889–1894.
11. http://www.hittite.com/product_info/product_specs/amplifiers/hmc481mp86.pdf.
12. http://www.minicircuits.com/.
13. http://www.hittite.com/product_info/product_specs/mixers/hmc483ms8g.pdf.
14. http://www.psi.au.com.
15. http://www.wenzel.com.
Uros Mavric received his BS degree in electrical engineering from the University of Ljubljana, Slovenia, and has been involved in particle accelerator physics ever since. He worked as a junior researcher at Instrumentation Technologies, Slovenia, for three years. In 2005, he won a scholarship at the Fermi National Accelerator Laboratory, where he is presently working on his PhD thesis. He has been involved in the design of the analog receiver and transmitter for the International Linear Collider main LINAC LLRF control system.
Brian Chase received his BS degree from the Illinois Institute of Technology in 1992. He is the group leader for RF control systems in the Accelerator Division at Fermi National Accelerator Laboratory. He is currently involved in the global design effort of the International Linear Collider. His research interests include digital processing schemes for precision closed loop RF control.
