Simplifying Digital Receiver Design with Direct Sampling

Figure 3 (a) Typical heterodyne receiver block diagram. (b) Typical direct sampling receiver block diagram.
Filters are essential components that protect a radar receiver. These small passive components do a big job; they clean up the signal “messes” created either outside the radar or made by the radar itself. While a typical heterodyne receiver requires multiple filters to clean up these messes, direct sampling is a technique that can be implemented in a digital array to directly convert analog signals to a digital format without using an IF conversion stage. As a result, direct sampling eliminates the need for a mixer and an amplifier in the receiver, along with the filtering required by those functions. This reduces the size of the receiver. To illustrate these benefits, Figure 3a shows a block diagram of a typical heterodyne receiver. Figure 3b shows the block diagram for a direct sampling receiver, which achieves the same system function with far fewer components.
In a direct sampling receiver, one filter selects the correct band of interest. It removes out-of-band interference and another filter cleans up any interference generated by the amplifier, along with selecting the alias bands of the ADC. It is important to note that these filters should be small, under a half-wavelength at the frequency of interest. As radar systems move to higher frequencies, filters need to become even smaller. Additionally, a multi-mission receiver will typically require switching from wideband to narrowband coverage or keeping operating frequencies away from frequencies to avoid. Protecting the receiver over its range of applications requires a small, agile filter bank and the physical dimensions of the entire filter bank must be less than a half-wavelength.
Miniaturizing Filter Technology

As the operational frequencies of radar targets of interest increase, the wavelengths of these signals become shorter. As described earlier, half-wavelength element spacing optimizes antenna performance, so arrays are also becoming denser as operational frequencies increase. Table 1 shows half-wavelength distances in free space for the upper-frequency range for some common bands.
As array density increases, it becomes even more critical to have the ability to steer beams to avoid interference, especially when transmitting signals. This raises an interesting question: instead of solely relying on reducing the size of filters, what if a filter could alter the speed of the signal in the material? Doing this effectively changes the wavelength. Equation 1 shows the classic equation that relates the frequency and wavelength of a signal to the speed of light in free space.

Where:
c = speed of light in free space
ν = frequency
λ = wavelength
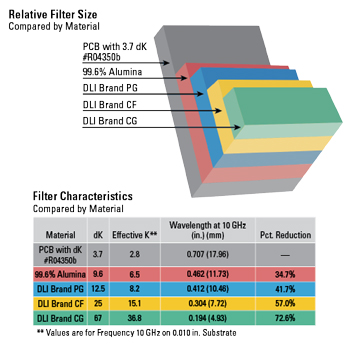
Figure 4 A comparison of the size and filter characteristics for different dielectric materials.
Equation 1 shows how it is possible to change the speed of a signal in a material. Using different materials makes it possible to change c to the velocity of propagation in the material. Changing the speed of the electromagnetic wave for a given frequency results in a different wavelength. Fortunately, when manufacturing distributed element filters on microstrip, for example, these filters will only occupy a fraction of a wavelength. If the wavelength in the material can be reduced, the size of the filter will decrease. For a microstrip line, the wavelength is determined using Equation 2:

Where:
Λ = Wavelength in microstrip
λ = Free-space wavelength
εeff = Effective dielectric constant, which depends on the dielectric constant of the substrate material and the physical dimensions of the microstrip line.
This equation shows how changing the substrate and the dielectric constant can impact the wavelength inside the microstrip filter.
Shrinking the Switched Filter Bank
While switched filter banks are traditionally associated with larger footprints, the same concepts described above can be applied to this technology as well. Filter manufacturers such as Knowles Precision Devices are leveraging materials science innovations to shrink the size of each filter. Then, using high-precision lithographic processes, these microstrip filters can be patterned onto custom ceramics, resulting in significantly reduced filter form factors. Figure 4 shows an example of this technique and the size reduction possible with printed circuit board (PCB), alumina and three custom dielectric materials. Beyond miniaturizing filter components to meet emerging requirements, there is also an opportunity for innovation in the packaging of the switched filter bank. With consideration for input size and how narrow an output needs to be, a designer has room for more channels. Figure 5 shows a four-channel filter bank design that features a 3D-stacked structure with alternating filters and interposer boards mounted directly to the PCB. This packaging concept reduces internal spacing, which ultimately reduces the size of the filter bank.
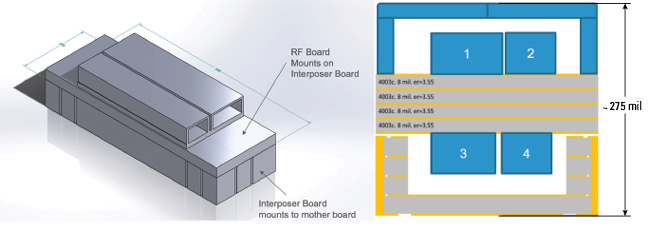
Figure 5 Using a 3D-stacked structure to reduce the size of a four-channel filter.
Important RF Considerations for Radar Filters
Beyond bandwidth capabilities and size, several important factors must be considered when selecting the filters to include in a switched filter bank for a radar system. This next section explores how temperature stability, tolerance and phase performance can impact filter performance.
Temperature Stability
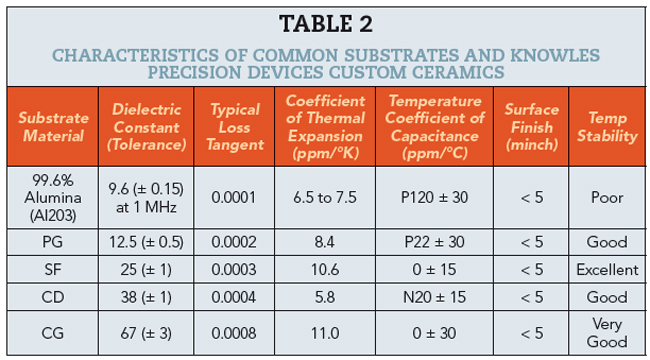
When selecting filter types and materials, the effects of the operating environment on filter performance must be considered. For microstrip filters, temperature stability is a crucial contributor to the frequency stability of the filter. In turn, the properties of the substrate materials are vital contributors to temperature stability. Let’s consider this comparison of characteristics, including temperature stability, for filters built on two common substrates, alumina and PG and three custom Knowles Precision Devices ceramics. The results are shown in Table 2.
Manufacturing Tolerances
It is also essential to analyze manufacturing tolerances when selecting filters for a switched filter bank in a radar system. Manufacturing tolerance refers to the acceptable deviation from the specified design parameters during the manufacturing process. For example, suppose a manufacturer specifies that a filter’s center frequency is 2.4 GHz with a ±100 MHz tolerance. In that case, the actual center frequency can only range from 2.3 GHz to 2.5 GHz to still be considered acceptable. Manufacturing tolerances impact filter performance, especially at higher frequencies where tolerance impacts can become significant. If a radar system needs to operate precisely and reliably at higher frequencies, it is worthwhile to consider selecting filters with tighter tolerances.
Phase Performance
Characterizing phase is an important and often overlooked aspect of assessing filter performance. Phase performance relates to how a filter affects the phase of the signals passing through the filter. Since filters can introduce phase shifts to the signals, good phase performance means not introducing much, if any, additional phase shift. This is essential for maintaining the integrity of the signals passing through a filter. Some factors to consider when specifying or characterizing phase performance:
- Phase linearity: This is a measure of the linearity of the filter’s phase response across its passband. Any nonlinearity in the phase response can distort the processed signals.
- Phase stability over temperature: Minimizing the phase variability over a range of temperatures allows for more accurate measurements and reduces calibration requirements.
- Phase length repeatability: Consistency over variables such as temperature, frequency and repeatability contribute to increased signal coherence, image quality and measurement accuracy.
Embracing Fully Digital Phased Array Technology for Radar
To meet the challenges presented by modern signal monitoring, designers need to consider fully digital beamforming techniques. When using fully digital phased arrays, each antenna element becomes independently controllable, enabling complex beamforming algorithms and multi-mission functionality. The result is emerging and planned radar systems with unprecedented flexibility and capability.
As the article has discussed, this transition to fully digital beamforming presents its own set of challenges, particularly when it comes to filtering solutions that provide the required performance in these compact, multi-mission systems. However, with recent advancements in materials science, filter components can be made in much smaller form factors, allowing designers to develop compact switched filter banks without sacrificing performance. Now, agile radar systems that take advantage of fully digital beamforming technology hold tremendous potential for meeting the evolving demands of aerospace, defense and public safety applications.

