If the phase noise error is small, then the composite performance breaks down to an intended signal plus an error term, which includes an average phase shift that equally affects all subcarriers. The judicious use of a pilot signal to calibrate the average error will eliminate the error term. The remaining error term is the phase noise impact from each subcarrier that impairs all of the others. This error is the ICI that is responsible for the loss of orthogonality.
There are a few options to characterize the degradation of the system caused by noise. Common methods examine the bit error rate, signal-to-noise ratio (SNR) degradation or EVM degradation. Equation 7 shows the EVM degradation as a function of phase noise variance and energy per bit over noise (Eb/No). The parameter M designates the number of bits per symbol. Other factors related to quadrature mismatch, frequency error and linearity degradation do affect EVM performance; however, this analysis focuses on just the phase noise impact on the system.

HOW CLOCK OPTIONS AFFECT INTEGRATED PHASE NOISE
For an RF-sampling transceiver solution, the modulated signal is directly output to the RF band; the high frequency sample clock introduces phase noise error into the system. To test the effect of clock options, we used the Texas Instruments LMX2820 integrated RF synthesizer in standard mode using its internal voltage-controlled oscillator (VCO), along with two alternative configurations. The first alternative substitutes the internal VCO with a lower phase noise external dielectric resonator VCO. The second alternative substitutes the internal N-divider with an external mixer to generate a phase frequency detector tone. Figure 2 shows the measured phase noise response of the three alternatives operating at 9 GHz.
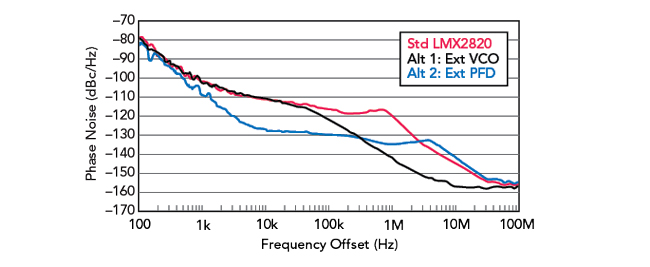
Figure 2 LMX2820 phase noise response with alternative configurations.
BW, the OFDM signal bandwidth and number of carriers, N, determine the proper limits of phase noise integration according to Equations 8a and 8b:


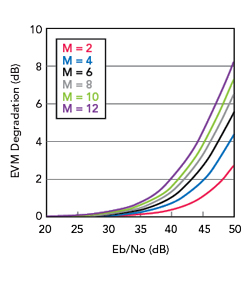
Figure 3 Error vector magnitude degradation vs. Eb/No over M.
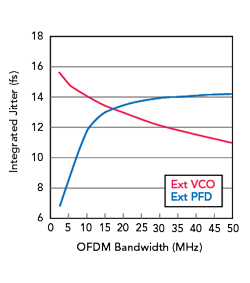
Figure 4 Integrated jitter vs. OFDM bandwidth using 1000 subcarriers at 9 GHz.
Figure 3 shows the EVM degradation as a function of Eb/No over the variance of the standard LMX2820 phase noise across constellations ranging from quadrature phase shift keying to 4096-ary (M = 2 to 12) using a 20 MHz wide LTE-like OFDM signal with 1200 subcarriers. The limits of integration are 7.5 kHz and 10 MHz. The phase noise performance becomes more important as the SNR requirement increases and the constellation of points grows. Since the inherent performance is already quite good, the degradation only becomes apparent at high constellation rates with stringent SNR requirements.
The alternative LMX2820 configurations both have improved phase noise performance compared to the standard mode, but each has a different shape across frequency. It is possible to exploit these differences when operating with a real world OFDM signal. The combination of bandwidths and number of carriers is infinite. This analysis centers on cases with 1000 subcarriers and the bandwidth varying from 10 to 100 MHz, which corresponds to a subcarrier frequency spacing ranging from 10 to 100 kHz.
Figure 4 shows the phase noise jitter calculated at 9 GHz across the OFDM bandwidth over the two alternative configurations. The first alternative provides better phase noise performance for signals with wider bandwidth and larger spacing, given the improved phase noise performance of the VCO at higher frequency offsets. The second alternative offers better performance for narrow bandwidth signals and tighter frequency spacing from the improved phase noise at close-in offsets. Applying the proper integration limits for a given OFDM configuration offers insight into the best clock topology to yield the least EVM degradation.
CONCLUSION
The phase noise analysis properly determines the impact of a specific clock source on the overall performance integrity of an arbitrary OFDM radar or communication system. The OFDM bandwidth and number of subcarriers set the proper frequency limits of integration of the clock phase noise response. The calculated phase noise variance determines the expected EVM degradation.
The clocking device options presented here have very low phase noise and introduce minimal error. Lower-performing clock sources have a more profound effect. Understanding specifically how the phase noise response translates to the phase noise variance for a given OFDM configuration enhances flexibility when determining the clock specifications.
Additional Resources
- A. G. Armada and M. Calvo, “Phase Noise and Sub-Carrier Spacing Effects on the Performance of an OFDM Communication System,” IEEE Communications Letters 2, No. 1, January 1998, pp. 11–13.
- A. G. Armada, “Understanding the Effects of Phase Noise in Orthogonal Frequency Division Multiplexing (OFDM),” IEEE Transactions on Broadcasting 47, No. 2, June 2001, pp. 153–159.
- G. Lellouch, “Waveform Design and Processing Techniques in OFDM Radar,” Ph.D. Dissertation, University of Cape Town, 2015.
- T. Pollet, M. Van Bladel and M. Moeneclaey, “BER Sensitivity of OFDM Systems to Carrier Frequency Offset and Wiener Phase Noise,” IEEE Transactions on Communications 43, No. 2, February 1995, pp. 191–193.
- V. Fialho, F. Azevedo, F. Fortes and M. Vieir, “OFDM Inter-Carrier Interference Due to Radio Frequency Synthesizer Phase Noise,” Conference on Electronics, Telecommunications and Computers (CETC), December 2013, pp. 608–616.
- R. Hoppenstein, “LMX2820 RF Synthesizer Phase Noise Improvement with Alternative Topologies,” Texas Instruments, 2022.
