Determining the Broadwall Dimension

To a large extent, the performance of a waveguide is determined by a, its broadwall dimension. Ideally, this dimension would be determined through mechanical measurement, but for sub-THz waveguides, it is not possible to measure the broadwall dimension in this way. The very small internal dimensions leave much of the length inaccessible to mechanical measurement methods. However, an estimate for an effective value of a can be determined by other means.

The electrical length, l_e, of a 2-port device can be derived from its unwrapped transmission phase response, φ, using Equation 3:

where λ_g is the guide wavelength at the measurement frequency, calculated using:

where λ is the free space wavelength. The lengths of the waveguide sections were also determined mechanically, acting here as the known values of length for each waveguide section. As found in a similar investigation,⁹ the results of the electrical length calculation are particularly sensitive to the assumed value of a used in the equation.⁴ Use of the nominal value of a can give electrical length results that vary significantly from the mechanical length. Therefore, to perform an effective calculation of the electrical length, estimates of a for each section were obtained using a minimization technique. The electrical lengths of the sections were calculated using Equations (3) and (4), using a value of a that minimizes the difference between the electrical and mechanical results.

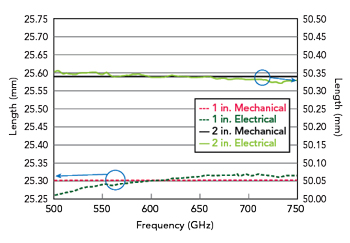
Figure 8 Mechanical and derived electrical lengths of the Flann sections.

The outcome from this process gave a value of a = 378 μm for both the 1 in. and 2 in. sections. For the WM-380 waveguide, the nominal value for a is 380 μm. This value of a is well within the expected tolerance of this dimension, which is expected to be around 10 μm for this waveguide size. The determinations of the electrical lengths of the sections using this estimate for a are plotted in Figure 8 along with the mechanical measurements of the two sections. The mean values of the electrical results agree with the mechanical results to within 10 μm. These results further indicate the successful manufacture of these THz waveguides.

CONCLUSION

Waveguide sections for the WM-380-band have been developed by Flann Microwave. They feature a seamless design and they have been benchmarked through the analysis of electrical measurements conducted at NPL. When compared with sections manufactured by VDI, the current industry standard and with modeled results, the measured results showed very good performance. These outcomes show great promise for this design technique to be applied to straights, bends and twists for waveguide component operation up to 1.1 THz. These components are now in development.

ACKNOWLEDGMENTS

The authors would like to thank Jeffrey Hesler of VDI for his cooperation with this work. This work was supported by the U.K. Government’s Department for Science, Innovation & Technology (DSIT) through the National Measurement System program.

References

1. S. S. Dhillon et al., “The 2017 Terahertz Science and Technology Roadmap,” J. Phys. D: Applied Physics, Vol. 50, No. 4, 043001, February 2017.
2. A. Leitenstorfer et al., “The 2023 Terahertz Science and Technology Roadmap,” J. Phys. D: Applied Physics, Vol. 56, 223001, April 2023.
3. T. W. Crowe, B. Foley, S. Durant, K. Hui, Y. Duan and J. L. Hesler, “VNA Frequency Extenders to 1.1 THz,” International Conference on Infrared, Millimeter, and Terahertz Waves, 2011, pp. 1–1.
4. “IEEE Standard for Rectangular Metallic Waveguides and Their Interfaces for Frequencies of 110 GHz and Above—Part 1: Frequency Bands and Waveguide Dimensions,” IEEE Std 1785.1-2012, March 2013.
5. “IEEE Standard for Rectangular Metallic Waveguides and Their Interfaces for Frequencies of 110 GHz and Above—Part 2: Waveguide Interfaces,” IEEE Std 1785.2-2016, Sept. 2016.
6. J. Skinner et al., “Interlaboratory Comparison of S-parameter Measurements in WM-570 Waveguide at Frequencies from 325 GHz to 500 GHz,” NPL Report TQE 24, National Physical Laboratory, July 2022.
7. J. Skinner et al., “Interlaboratory Comparison of S-parameter Measurements in WM-380 Waveguide at Frequencies from 500 GHz to 750 GHz” NPL Report TQE 23, National Physical Laboratory, July 2022.
8. “Sub-Millimetre Seamless Waveguide,” Flann Microwave, Web: https://flann.com/wp-content/uploads/2022/03/Sub-Millimetre-Seamless-Waveguide-Datasheet-Revision-3.pdf.
9. N. M. Ridler et al., “Establishing Waveguide Lines as Primary Standards for Scattering Parameter Measurements at Submillimetre Wavelengths,” Metrologia, Vol. 58, No. 1, Art. No. 015015, February 2021.
10. G. F. Engen and C. A. Hoer, “Thru-reflect-line: An Improved Technique for Calibrating the Dual Six-port Automatic Network Analyzer,” IEEE Trans. Microwave Theory Tech., Vol. 27, No. 12, pp. 987-993, Dec. 1979.
11. N. M. Ridler, “Choosing Line Lengths for Calibrating Waveguide Vector Network Analysers at Millimetre and Sub-millimetre Wavelengths,” NPL Report TQE 5, National Physical Laboratory, March 2009.
12. N. M. Ridler et al., “Strategies for Traceable Submillimeter-Wave Vector Network Analyzer,” IEEE Trans. Terahertz Science and Technology, Vol. 9, No. 4, pp. 392-398, July 2019.
13. T. Probst et al., “Good Practice Guide on Rectangular Waveguide Connections above 100 GHz,” PTB, July 2019.
14. J. Sun, F. Hu and S. Lucyszyn, “Predicting Atmospheric Attenuation Under Pristine Conditions Between 0.1 and 100 THz,” IEEE Access, Vol. 4, pp 9377–9399, 2016.
15. D. M. Kerns and R. W. Beatty, “Basic Theory of Waveguide Junctions and Introductory Microwave Network Analysis,” Pergamon, 1967.
16. N. M. Ridler and C. Li, “Benchmarking Electrical Loss in Rectangular Metallic Waveguide at Submillimeter Wavelengths,” Proceedings of 2017 UK/Europe-China Workshop on Millimetre-Waves and Terahertz Technologies (UCMMT 2017), September 2017.