The development of 3G services is requiring a constant increase in network capacity from the mobile operator. Dense access microwave networks, in terms of links per square kilometer and spectrum occupancy, are needed to connect UMTS nodes to the core network. Any introduction of a new link or any capacity upgrade needs careful planning and the choice of the RF channel is crucial. When looking for a vacant channel in the radio frequency spectrum, the normal practice suggests the use of small and portable field measurement setups, normally consisting of a simple receiver (antenna, low noise amplifier and spectrum analyzer). More complex systems can be conceived, of course, but the radio network engineer is mainly driven by operative and economic constrains. Nevertheless, the radio link planner should be aware of the limits of these measurement systems.

In this article, these specific measurement benches will be analyzed in terms of sensitivities achievable in the field and their limitations with regards to interference detection and their impact on system planning. It is meaningful to have some basis for comparison between interferer levels that could degrade the link quality and the effective levels that it is possible to detect when assessing radio spectrum occupancy. Hence, how interferences affect digital radio links will be reviewed first.
The “Victim” of Interference

A single radio terminal, part of a point-to-point digital radio link, will be considered as the potential victim of other digital interferers. Each of the two equipment terminals can be affected by interference in different ways, depending on the radio network environment into which the link itself is embedded. Generally, when referring to power levels, some reference points in the radio link plant are defined; the usual point corresponds to the connection between the branching network and the antenna feeder (point C in Figure 1 of the receiver chain). For split mount equipment (indoor plus outdoor units) this is the only RF point available from outside the unit.
The receiver threshold
The thermal threshold of a receiver system is the minimum power level, at the apparatus input, that guaranties a bit error rate (BER) better than a certain value (typically BER = 10–6). The threshold is an important receiver parameter in link budget analysis since it impacts on the link performance. The receiver threshold level PRX0 (at point C) depends on the system’s modulation scheme, bit rate, front-end noise figure and implementation losses


where
(S/N)10–6 [dB] = signal-to-noise ratio required at the demodulator input in order to have BER=10–6
NRX [dBm] = thermal noise level
Limp [dB] = a positive term that includes noise figure and modem implementation losses (industrial margin); typically in the range 0.5 to 2 dB
RS [MHz] = symbol rate
Fnoise [dB] = receiver noise figure
Examples of threshold values are reported in Table 1, for point-to-point microwave systems operating in the 18 GHz frequency band. The European Telecommunications Standard Institute (ETSI) also gives values for various equipment types in different frequency bands.1
Effects of Interferences
The effects of interferences on a digital radio relay system are normally quantified in terms of threshold degradation (see Figure 2). If no interference is affecting the receiver, the BER curve corresponds to the additive white Gaussian noise (AWGN) channel condition (I = –∞ dBm). In the presence of interference, the BER curve widens (I = I(δ)) since the receiver needs more power to maintain the same S/N ratio at the demodulator in order to have the same target BER. Hence, the operating point with BER = 10–6 will be found at the degraded threshold PRX0 + δ.
The signal-to-noise ratio for this new point corresponds to the degraded threshold over the power sum of the receiver noise level NRX (dBm), plus the interference level I (dBm), which must be equal to (S/N)10–6, that is

This formula gives the threshold degradation δ in terms of the receiver noise and the interference level at point C. If more interference sources are present, I is the power sum of all components, supposed uncorrelated.
A δ = 3 dB degradation is obtained when the interferer level is equal to the receiver noise (I = NRX), while δ = 1 dB degradation is obtained when the interferer level is 6 dB below the receiver noise level. A degradation equal or lower than 1 dB is normally accepted, especially in a much polluted electromagnetic environment. Undue degradations (above 3 dB, for example) mean that some further optimization in the design of the link has to be considered.
Compare now the working C/I ratio with respect to the target S/N ratio, for a fixed BER. The carrier level for the degraded case is
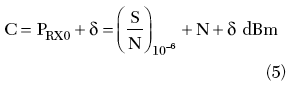
Then, the C/I ratio, the S/N target and the threshold degradation are combined as

The threshold degradation is given by

in terms of (S/N)10–6 (equipment parameter) and C/I ratio (link working point).
For instance, the C/I ratio corresponding to a 1 dB degradation is
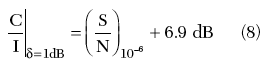
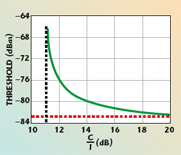
This particular C/I value is often given as a system specification for co-channel and adjacent-channel interference rejection1 and it is sometimes useful to relate it to the (S/N)10–6. From Equation 7 it is clear that, as C/I approaches (S/N)10–6, the threshold degradation increases with no limit; the system cannot work with a BER better than or equal to 10–6 at C/I = (S/N)10–6. Figure 3 shows the effects of the interference in terms of the degradation curve for a 4QAM system with a receiver thermal threshold equal to –83 dBm at BER = 10–6 (16 × E1 capacity).
In order to design the test bench to be used in the field to detect dangerous interferer levels, the interferer levels that can be considered to effectively degrade the receiver threshold of a radio link must be found. From Equation 7, the interferer level that gives a fixed maximum accepted degradation δ is
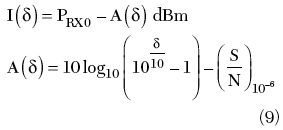
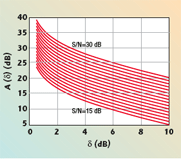
Figure 4 shows the term A(δ), which indicates the difference (in dB) between the interferer level and the thermal threshold, in order to give δ dB degradation. For instance, if (S/N)10–6 = 26 dB and Prx0 = –70 dBm, A = 31.8 dB for δ = 1 dB, so an interferer of about –102 dBm is sufficient to give a 1 dB degradation on the receiver threshold.
For the two commonly used degradation values, the practical rules are
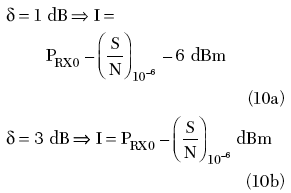
To some extent, this analysis is a little pessimistic. In Equation 4, the thermal noise and the digital modulation interferer are combined in a fashion that is correct only if the interferer is assumed to be a Gaussian stochastic signal. This is the case when the interference term I is the sum of many independent interferers. Normally a single digital interferer has a non-Gaussian statistic and the threshold of degradation is slightly less. In other terms, the same threshold degradations as in Equation 10 shall be produced by a single digital interferer 1 or 2 dB higher.

Field Detection of Interferers
A trustworthy way to measure the real impact of the interfering environment on a certain radio link is to use the radio link equipment itself. A typical procedure to evaluate the threshold degradation is to simulate a fading on the transmitting side and measure at the receiver the power level that corresponds to BER = 10–6. The degradation is the difference between the threshold measured in the field and the value obtained from laboratory measurements or system specifications. This procedure is reliable, but needs the radio link to be already installed. It can be used at the commissioning of the link as a further test, but it is very impractical in the link-planning phase. A measurement bench built with a portable spectrum analyzer, a low noise amplifier and a small antenna is a much more flexible and cost-effective system.
The Measurement System
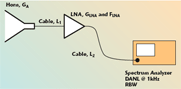
The measurement system to be investigated is shown in Figure 5. The system is composed of a microwave antenna tuned in the relevant frequency band, a low noise amplifier (LNA) and a portable spectrum analyzer (SA). The antenna, typically a small horn reflector, and the LNA are connected by a RF cable that should be as short as possible. Another cable connects the LNA to the analyzer.
Noise Analysis
In order to evaluate the minimum interferer signal that the system can detect, the overall system noise is evaluated. The noise sources affecting the system sensitivity include: the antenna noise (electromagnetic noise coming from the environment and captured by the antenna), the transmission line noise (mainly due to passive electric losses of the first cable) and the LNA noise (electronic and thermal noise). The SA input RF attenuator is not included in the analysis since it is generally set to 0 dB in order to have best displayed average noise level (DANL). Figure 6 shows all the noise sources in terms of noise temperature at the system input. The total system noise temperature TSYS is


where

expressed in terms of DANL at 1 kHz resolution bandwidth.
The antenna noise temperature, being at the starting point of the receiver chain, is one of the leading components of the system temperature. This term is the geometrical convolution of the brightness temperature of the surrounding environment and the antenna radiation pattern.
For instance, supposing a narrow beam width antenna pointed toward a region of uniform background noise temperature Tbg, then TA = Tbg. In Earth-Space communications, this could be the case of a ground station antenna directed to the sky (TA = 3 to 30 K in the microwave region up to 40 GHz) or the case of a satellite antenna pointed to the earth (TA = 290 K). Measurements of brightness temperature for a ground station receiver have been reported.2 For clear air conditions, at 0° elevation, the brightness temperature is approximately 90 K at 5 GHz, increases almost linearly to 290 K at approximately 20 GHz and then remains constant. For this specific case, considering that the measurements are made with a wide beam antenna (such as a 30° HPBW horn antenna) with no significant elevation angle, the antenna temperature is usually taken to be TA ~ T0 = 290 K.
Keeping in mind that GLNA is generally much higher than the total losses L1 + L2, the system temperature simplifies to


Furthermore, if the following condition is fulfilled

the system noise temperature is simply
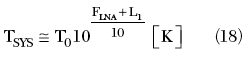
The total output thermal noise, displayed by the spectrum analyzer in a resolution bandwidth RBW (MHz), is

Equation 17 means that the noise provided by the LNA to the SA shall be at least 10 dB higher than the SA effective noise. This condition is often fulfilled by a good amplifier chain.
The minimum detectable level
Searching for digital radio sources, it is very likely to come across noise-like signals with a flat power spectrum density. The emitted power of these interferers is spread over the entire signal bandwidth and their spectral density tends to be buried in the noise. The interferer level measured by the SA is
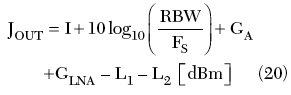
where
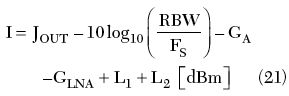
RBW (MHz) = SA resolution bandwidth
FS (MHz) = Nyquist symbol rate of the interferer signal
I (dBm) = interferer level captured by the antenna
The level of the interferer captured by the measurement antenna is
![]()
The level is referred to a virtual point before the measurement antenna. To evaluate its effect on the microwave link, it must be scaled to the reference point C, adding the link antenna gain GRL and the feeder losses LF

where (θ,Φ) is the polar direction of the incoming interferer. The interferer-to-noise ratio referred at the SA is

which is valid according to Equation 17.
To be detectable with respect to the system noise floor, the (J/N)OUT ratio should be at least zero. In this situation, the detected signal appears on the SA as a 2 dB spectrum bump over the average background noise.3 The minimum detectable interferer level IMDL at the antenna is then

For wideband signals, with a symbol rate much wider than the resolution bandwidth, the sensitivity of the measurement system is determined by the interferer bandwidth, the LNA noise figure and the net antenna gain (including the first cable loss). The RBW has no influence, since it processes wideband signals and noise the same way. Furthermore, if Equation 17 is fulfilled, even the LNA gain has no impact on the bench sensitivity. IMDL has be be scaled as well to the reference point C


A “bad” variation on the theme
If the performance of a bench is analyzed without the LNA, the SA is connected directly to the measurement antenna via a single RF cable (loss L1) and the output noise displayed on the SA is

The measured interferer-to-noise ratio is

Then, the minimum detectable interferer level IMDL at the antenna is

It is clear that the term FLNA of Equation 24 has been replaced by the term FSA = DANL1kHz + 144, the former being the SA noise figure. The test bench without LNA has a drastically reduced sensitivity by FSA – FLNA. This severe reduction may correspond to dozens of dBs (30 dB or more); benches without a proper LNA could not detect strong interferers and the measurement session may become meaningless.
Some Measurement Aspects
When searching for wideband digital interferers, reducing RBW does not significantly help the system sensitivity. So the choice of RBW is mainly driven by the sweep time of the SA. A complete interference search at each radio site often means scanning the whole spectrum band (both lower and upper sidebands) from 0° to 360° azimuth at both polarizations, at steps equal to the measurement antenna half power beam width. This corresponds to hundreds of SA snapshots and the time consumed for each of them is crucial. From a practical experience, a RBW of 300 kHz seems to be a suitable trade off between spectral resolution and sweep time, at least for microwave digital radio relay systems. If narrowband signals are to be investigated (that is analog signals with discrete spectrum lines or non-modulated carriers), smaller resolution bandwidths can be a better choice.
Video bandwidth (VBW) is another SA setting. It does not affect the noise floor but averages the display trace, making the inspection easier. Since it affects the sweep time, a good choice can be VBW = 30 kHz.
If DANL is not known at 1 kHz, it is possible to scale it from
With the equipment at hand, it is a good idea to measure DANL in the frequency range of interest using a 50 Ω load to terminate the SA input. The level of the flat trace indicated by the SA with RBW set to 1 kHz is exactly DANL1kHz. Equation 17 can be verified by terminating the LNA input with a 50 Ω load just before the antenna flange. If the new background noise level measured is at least 10 dB above the SA DANL1kHz, Equation 17 is verified and Equation 24 is valid.
A Practical Example
Consider a test bench used in the field for real radio spectrum analysis in the 18 GHz frequency band. Specifically, a 55 MHz free channel is identified in order to deploy a 1×STM-1 32 TCM link with radio parameters taken from Table 1 and with 0.6 m parabolic integrated antennas on each side.
The measurement system is composed of a horn antenna (GA = 23 dBi) and an LNA (GLNA = 45 dB, FLNA = 2 dB) directly connected to the antenna flange (L1 = 0 dB). The SA (Agilent E4407B) is connected to the LNA via a coaxial cable (L2 = 2 dB).
Equation 17 is fulfilled (DANL1kHz = –112 dBm); from Equation 19, the predicted noise background is –74.2 dBm. The system noise is measured closing the LNA input with a matched attenuator and the average noise background is about –76 dBm in 300 kHz RBW, as shown in Figure 7. Taking into account a –2.5 dB factor (due to the under-response of the SA log-scale) and an over-response of +0.5 dB (ratio of the equivalent noise bandwidth to the –3 dB bandwidth), the corrected measurement agrees with the predicted value (–76 + 2.5 – 0.5). With this setup, the maximum interferer level IMDL is reported in Table 2 for different interferer bandwidths.
It is interesting now to compare these values with interferer levels that can be considered dangerous for the planned radio link. Assuming that an interferer is considered dangerous if δ = 3 dB, from Table 1 and Equation 10a, the maximum interferer level IMAX that it can tolerate is –93.6 dBm. If the δ = 1 dB criteria is used, the IMAX level would be 6 dB lower.
The IMAX level is referred at point C, while measurement setup sensitivity IMDL is the level detected prior to the measurement antenna. Equation 25 must be used to compare the two of them.
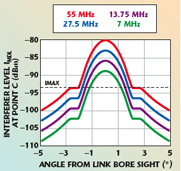
In this example, GRL = 38 dBi at the antenna boresight and LFC = 0 dB. For a gain at an angle direction the antenna radiation pattern has to be used. Here, an approximation of the beam, valid for small angles, was used. The IMDL at C is reported in Table 3 (link direction). All the values referred to the direction of the link are greater than the maximum acceptable interferer level. Angled interferers will be discriminated by the radio link antenna. The difference between the bench sensitivity IMDL at C and the maximum acceptable interferer level IMAX is significant only in the angular region close to the link direction. Figure 8 shows the IMDL at C of Table 3, scaled by the angular discrimination of the antenna link.
Consider the 55 MHz interferer (the hardest to detect because of more spread over the bandwidth). In the angular sector of ±2° with respect to the link direction, the IMDL is greater than IMAX. In other words, the antenna link is not able to discriminate those “hidden” (undetected) interferers. If they are present, they can effectively degrade the link (see Figure 9). Outside this region, possible undetected interferers reaching terminal A will be reduced down to values that will respect the threshold degradation criteria. For narrower band interferers, the indeterminate angular region is also narrower (that is ±1° at 7 MHz). From Equation 24, it can be seen that not much can be done in order to increase the sensitivity except by changing the measurement antenna. For instance, a 30 cm parabolic antenna could be used, at least for the measurements along the link direction. With this new antenna, the sensitivity could have been increased by 11 dB. However, when performing measurements in the field, it is not always feasible to use a high gain antenna; this is especially true for the lower frequency bands such as 7 or 11 GHz. It is then up to the radio network designer to investigate the hidden interferer’s geographical region, in order to find distant interfering sources (radio towers, microwave hubs, etc).
Conclusion
In this article, a specific measurement bench was analyzed for in field interference detection used in the planning and design of microwave digital radio links in a polluted electromagnetic environment, where detailed spectrum analysis is needed. The test bench considered is composed of a simple portable receiver scheme suitable for field operation. A quick noise analysis has been provided in order to evaluate the measurement performance in terms of achievable sensitivities. With equipment commercially available, it is possible to achieve good confidence in the search of interferers.
Nevertheless, these systems have inherent limitations that should be understood by the radio link designer in order to perform correct radio link planning and spectrum management. The impact of these limitations has been investigated in terms of angular regions, where the antenna link is not able to discriminate “hidden” interferer signals that can effectively degrade the link.
References
1. Generic Wordings for Standards on DFRS Characteristics – Part 1, European Telecommunications Standard Institute, TR 101 0361-1, 2002.
2. Recommendation P.327, Radio Noise, International Telecommunication Union-Radiocommunications, Geneva, Switzerland, 2001.
3. C. Brown, Spectrum Analysis Basics Seminar, Hewlett-Packard, 1997.
Luca Stroppolo received his MS degree in electronic engineering from the II University of Rome Tor Vergata in 1993. In 1995, he received his postgraduate degree from the SSGRR School of Telecommunication of STET, where he subsequently taught courses on wireless systems aspects. From 1995 to 2001, he was with the network engineering department of Telecom Italia, where he was involved with the specifications and system analysis of wireless systems (point-to-multipoint systems and wireless LAN) including testing and field trials. During that time he was also a member of the ETSI TM4 standardization group. From 2001 to 2002, he was with Edisontel, responsible for the deployment of the radio access network. From 2002 to 2005, he was with 3 Italia in the radio network-planning department, responsible for microwave radio link design and system engineering. Since 2006, he has been working with Ericsson NSI, responsible for radio access network planning and design.
