Traditional capacitor and inductor models have consisted of two or three elements (capacitor examples are shown in Figure 1). The two-element models provide a simple way to define the device. From a circuit designer's viewpoint, the two-element models may suffice for applications where the component is being used at frequencies well below self-resonance and/or in not so demanding applications. From a component manufacturer's perspective, the two-element models provide basic information about their component to the users and allow them to verify device values and do bin-sorting of the devices in production tests.

The three-element models provide more insight into the component's actual behavior, especially as the component is used near its self-resonant frequency. The threshold of being "near" the self-resonant frequency is often considered when the application frequency is greater than a tenth of the self-resonant frequency. Table 1 shows the capacitance value results, using a two-element model (Cp, Rp) for a 560 pF capacitor as it approaches self-resonance. The flaw in the model is evident.

Figure 2 shows the two- and three-element models for typical inductors. As in the case of capacitors, there are two two-element models for the inductor (series and parallel), but there are also two three-element models for the inductor. These two models are applied to different types of inductors. Model A is used for inductors that have a relatively high core loss (such as toroidal choke inductors). Model B is used for inductors that have a relatively low core loss (such as typically RF and IF inductors). The two models differ by what is presumed to be the dominant sources of loss and stray capacitance.

The Need for More Sophisticated Models

While the three-element models provide much more insight than the two-element models, they still have limitations. In the case of inductors, the choice between model A or B is a discrete choice but real inductors will have some of the losses and capacitance represented by model A and some of those represented by model B. Inductors also have further complications because of the non-ideal nature of magnetic materials. For both inductors and capacitors, second-order effects also come into play, especially as the frequency increases. An example of this is the skin effect, which will cause the equivalent series resistance (ESR) of a device to increase with frequency (see a capacitor example in Figure 3).

Another reason for needing these more accurate models relates directly to market demands - the need for higher performance equipment and the need to achieve faster time to market. Knowing the actual component behavior allows the designer to achieve tighter tolerances. Figure 4 shows an example of how the phase noise of a VCO is affected by the Q of the capacitor. In other cases, not knowing the components actual behavior may cause reliability problems. Electronic design tools help achieve faster time to market but require that more accurate and thorough models be used so that simulation results agree with actual performance.

Developing More Advanced Models

A new technique has been developed for creating more advanced models. The approach is to actually use the electronic circuit design tools mentioned above. The first step is to accurately measure the component using an impedance analyzer (all measurement examples shown here have been done using the Agilent model E4991A 3 GHz impedance analyzer). While measurements could be made using a standard directional coupler or S-parameter test set-up, those measurement results will not be nearly as accurate and will limit the ability to find an accurate, more sophisticated model. Next, the topology of the more sophisticated proposed model must be outlined. For example, a frequency sensitive ESR factor may be included in the model.

Running the Simulation to Define the Sub-element Values

To find the specific values of the sub-elements in the proposed model, a circuit design and simulation software (in this case Agilent ADS) will be used. Using the design system, the proposed equivalent circuit will be built and one end of that component will be driven with an AC source. The other end of the device will go to a summation point. Next, another device will be defined by a measurement data file from the impedance analyzer. One end of this device will be driven by a source that is synchronous with the other source, but phase shifted by 180°. The other end of this "data-file device" will be connected to the summation point. The output of the summation point is sent to a null detector whose job is to try to keep the summation point voltage as close as possible to 0 V, as shown in Figure 5.

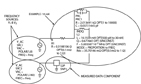
After this circuit has been set up, the simulation software is instructed to sweep the frequency and sweep each of the variables in the model with the goal to always drive the summation point to 0 V. At the end of the simulation, the design system returns the value of each of the sub-elements that optimized the condition to keep the summation point near 0 (that is to match the model sub-element values to the data file from the impedance analyzer).

Figure 6 shows a new model derived for a 10 nH RF inductor. The sub-element values in this display are derived by the simulation software. Figure 7 shows a first pass optimization of the element's values for the new model of a 10 nH inductor, compared with the measurement results. The element values derived from the simulation software at 2 GHz were determined to be R1 = 270 mΩ, R2 = 9.9 MΩ, C1 = 137 fF, L1 = 9.9 nH and R3 = 3.06 Ω. Figure 8 gives improved results after further tuning with R3 = 2.18 Ω.

Conclusion

More thorough and advanced models can be developed for passive devices. By using this new approach, the values and characteristics of the sub-elements in those models can be determined accurately.

Acknowledgment

The author wishes to thank Prakesh Gulrajani and others from the applications and research design teams in the Kobe, Japan facility.

Gregory L. Amorese received his BSEE degree from the Rochester Institute of Technology. He joined Hewlett-Packard in 1979, and in 1988 transferred to the Kobe Instrument Component Test Division to work as the company's product line manager at Hewlett-Packard's European Marketing Operation. In 1996, he moved to California to lead the Kobe Instrument Division's US operations. Currently, he is the program manager for component test within the Wireless Business Unit of Agilent Technologies, where he focuses on customer measurement and analysis needs of components for cellular phones and other wireless appliances.