The bead discussed in this article represents the dielectric structure for mechanical support of coaxial microwave components. The main features of the bead are its electrical performance and mechanical ability to keep all parts of the component together. The electrical performance includes low reflection and suppression of high mode resonances. The insertion loss caused by the dielectric is insignificant and usually does not influence performance due to the bead's relatively short length.
The mechanical properties are particularly important for precision adaptors because an adaptor should be able to withstand a large number of connect-disconnect cycles (typically many thousand). In typical coaxial components such as a connector or an adaptor, the bead is the only supporting structure of the center conductor. Some components contain more than one bead, either of the same or different shape.
There are many materials that can be used for dielectric supporting structures in microwave components. Traditional materials for bead manufacturing are Rexolite™ for precision adaptors, Noryl-PPO™ and Ultem™ for manufacturing grade adaptors and connectors, as well as Teflon™ for connectors and adaptors. Rexolite and Ultem are the strongest materials mechanically. Noryl and Ultem can either be machined or molded, which will reduce the price. Teflon has the lowest dielectric constant, lowest insertion loss and highest operating temperature (and therefore power handling), but it is the softest of these materials.
Ultem has the second highest operating temperature of 165°C and is strong mechanically. However, the dielectric constant of Ultem is approximately 3.05 at microwave frequencies, requiring a significant part of material to be removed, which is not always convenient. Rexolite and Noryl have a low maximum operating temperature of approximately 100°C and generally should not be used for components in military applications. For hostile environments some special materials can be used, an example being PEEK (polyetheretherketon). For the new bead design, Ultem was chosen as the best-suited dielectric material.
MODE RESONANCE
The ability of the bead to maintain a single mode operation in the component is an important part of the electrical performance. The principal mode alone (in this case TEM) is unable to satisfy the boundary conditions imposed by any discontinuity, including the bead. Every internal step in the transmission line generates higher modes of the transverse magnetic types. However, those modes are attenuated very fast. The main danger for transmission in a coaxial line is contained in the second mode type -- the transverse electric mode TE11 (in some references this mode has a designation H11 ). TE11 is a waveguide mode and therefore has a frequency-dependent impedance and velocity of propagation compared to TEM. A dual mode transmission is not desired in a coaxial line because of signal distortion. In addition, the second mode resonance can result in overvoltage and overheating in the transmission line. The second mode can propagate from one certain frequency often referred to as the cut-off frequency (or critical frequency). The approximate value of the TE11 cut-off frequency in a coaxial line can be calculated from
where
Fco = value of cut-off frequency in GHz
D = internal diameter of outer conductor in inches
d = external diameter of inner conductor in inches
ε = dielectric constant
Note that cut-off frequency typically does not imply the second mode transmission. It suggests the possibility of transmission. The resonant frequency is higher than the cut-off frequency and is highly dependent on the length of the bead. Calculations of the resonant frequency can be obtained from the work of H. Neubauer, et al.3
The field distribution for TEM and TE11 modes are shown in Figure 1. The second mode resonance can occur in the dielectric bead area or in the interface area (for Teflon loaded interfaces such as in SMA or TNC connectors) despite the short length of the dielectric region. Since an air-line has an inductive impedance at the frequencies of interest for the TE11 mode, the effective length of the bead is also increased by the reactive load, which can excite a resonance to occur even for relatively short beads. One method to suppress the resonance is to load the bead in low impedance lines.1 This method has been successfully used to push the operating frequency of special TNC connectors higher. Traditionally, the second mode resonance was particularly important for TNC2 because some military applications require high power connectors for extended frequencies. Some companies today are marketing special SMA connectors with extended frequencies up to 27 GHz. There are also reports devoted to the suppression of unwanted resonances in precision connectors and adaptors.3,4
|
|
It should be noted that the bead cannot be considered to be alone because there is another one in the mating connector. The short distance between the two beads can excite a resonance to occur.
It can be seen from the field distribution drawing that the TE11 mode does not have symmetry in the transverse plane. Thus, there are two important points to note: Any asymmetry in the radial plane can generate the second mode, and there is the possibility of two independent TE11 mode resonances in the different cross-perpendicular planes.
It is not always easy to detect the second mode resonance in a component. Jim Kubota2 noted that, in some cases, the second mode resonance should be excited. Besides, if the component passed the sweep test of reflection (SWR), it does not mean that the component, in this case a connector, is resonance free. It is necessary to screen the insertion loss (IL) for resonance using a frequency sweep. This conclusion is important. For example, the data depicted on Figure 2 comes from the test of an assembly with K connectors. The SWR curve does not show any significant mismatches up to 45 GHz; however, IL data shows a resonance at a frequency around 44 GHz.
|
|
It is not always easy to test for insertion loss because of the special fixtures required (panel mount connectors, for example). Besides, if the component is terminated in a non-ideal load, it could be an additional reason for the second mode resonance. A calibrated vector analyzer test-port is an excellent load for components and will not excite a resonance. This means that if the second mode resonance spikes are absent in the IL sweep test, it does not fully guarantee the same performance in real operation. In addition, a typical vector analyzer test-port contains 3.5 mm air-line connectors, which have a higher cut-off frequency (up to 36 GHz). It is convenient for the testing of SMA components but it does not reflect real use. Normally most SMA connectors will be connected to other SMA connectors. This connection reduces the resonance frequency to a lower value than the test situation. The standard (without any special features) SMA connector should not be specified for operation at frequencies higher than 25 GHz even if it does not have any visible resonance ripples on the IL and SWR curves. A typical (not precision) N connector with a Teflon insulator has a cut-off frequency at 10.4 GHz, but, according to military standards, should work up to 12.4 GHz. This specification can be a cause of problems for some applications, particularly if the Teflon bead has a significant length. Hermetically sealed components typically have a glass bead fired inside the connector body. The dielectric constant of glass is approximately two to three times that of Teflon. Thus the microwave glass-sealed components have a typical lower operation frequency because of the possibility of the second mode resonance.
H. Neubauer, et al.,3 have noted that waveguide resonances in straight lines arise from contact faults, particularly in the outer conductor. According to the authors, even a very slight irregularity of the outer conductor is enough to fulfill the condition for the generation of waveguide resonances. For this reason, it is important to keep some distance between the contact point on the connector and the bead. One additional note is that a push-on connector is more apt to show resonance compared to a threaded one.
Theoretically, it is not complicated to avoid the second mode -- just reduce the dielectric constant (and therefore radial dimensions) of the dielectric in the line and the cut-off frequency will increase. A typical example is the SMA 2.9 connector from Radiall, where the supporting bead for the 2.92 mm air-line has reduced radial dimensions.5 This connector is mode free up to the air-line cut-off frequency (in this case 46 GHz). However, this design is not convenient for all components and most standard dielectric beads (including precision items for 7, 3.5, 2.92 and 1.85 mm air-lines) are not mode free. Theoretically, the second mode can be excited. On the other hand, these components were designed so that the mode resonance would never happen, up to their highest operation frequency (for example, 18 GHz for 7 mm air-line). Some plug-connectors have a thick wall option on the interfaces, which can also push the operating frequency higher.6 Typically, the cut-off frequency of the bead is lower than the cut-off frequency of the air-line. The maximum operating frequency of the component is between these two values. The maximum operating frequency depends on the length of the bead. The closer the length of the bead approaches zero, the closer the maximum operating frequency approaches the cut-off frequency of the air-line. Consequently, the farther the length of the bead is from zero, the closer the maximum operating frequency approaches to the cut-off frequency of the bead.3
REFLECTION CONSIDERATIONS
The component with the lowest reflection consists of a coaxial air-line without any beads and steps. The bead can only increase reflection. Beadless lines have a wide use in metrology, but are inconvenient for manufacturing grade components.
The general equation for the reflection coefficient from two discontinuities is
where
in = total reflection coefficient at the reference plane
1 = reflection coefficient from the first discontinuity
2 = reflection coefficient from the second discontinuity
L1 = distance from the reference plane to first discontinuity
L2 = distance from the reference plane to the second discontinuity
ß = phase constant, ß = 2¼/λ
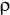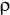According to W. Anderson et al.,11 for small reflections, waves travelling between discontinuities can be neglected ( 1 2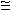 
0). This means that for small discontinuities the total reflection is zero if
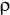2 = 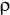1 e2jß(L2L1)
Thus the small discontinuity can be compensated for by the second one of equal magnitude but of the opposite sign (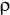 2 = 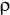1 ) in the same location (L2 = L1 ). In this case, the compensation occurs over a wide band because the frequency dependent parameter ß (L2 L1 ) is equal to zero. For example, the fringing capacitance can be compensated for by a series inductance and this compensation can be frequency independent.
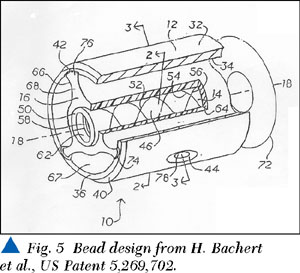
There are several patents and articles devoted to the design of microwave supporting structures with low reflection. Some examples are depicted in Figures 3, 4 and 5.7,8,9
|
|
|
|
|
|
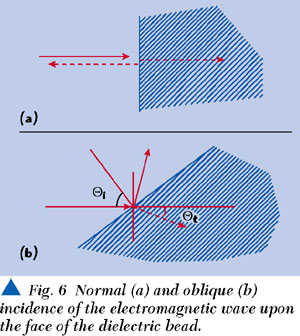
Most of the bead designs are similar. On the edges of the bead there are two short lines with high impedance for the fringing capacitance compensation. Along the bead there is a coaxial line with constant impedance equal to or close to the characteristic value (50 Ω for microwave transmission lines). Calculations of the fringing capacitance and compensation have been reported in the literature.10,11 The main difference between the designs is in how to keep constant impedance and avoid unwanted resonance at the same time. The typical design decision is to make holes in the dielectric, usually through it, in order to reduce the effective dielectric constant and to keep a constant impedance along the bead as shown in the patented designs. This kind of dielectric structure employs a normal incidence. It means that the Pointing's vector is perpendicular to the surface of incidence (in this case the plane of the bead). By definition, this vector has the direction of the cross-product of vectors E and H. Thus, in a coaxial line, the Pointing's vector is parallel to the center conductor, but the distribution of the Pointing's vector is not uniform. The Pointing's vector (and therefore the energy) in the coaxial line is densest near the center conductor. This fact will be important for the new design.
|
|
The oblique incidence, shown in Figure 6, can be successfully used to design the bead. The angles of oblique incidence can be calculated from Snellius' laws, and the complex magnitude can be calculated from Fresnel's equations.12 As it is known from optics, there are two different kinds of Fresnel equations: parallel polarization and perpendicular polarization. Here, parallel polarization means that vector E is parallel to the plane of incidence. Consequently, perpendicular polarization means that the direction of vector E is perpendicular to the plane of incidence. Fresnel's equations for both polarizations are
where
|
|
= |
reflection coefficient for perpendicular polarization |
|
|
= |
reflection coefficient for parallel polarization |
|
|
= |
angle of incidence |
|
|
= |
angle of refraction |
|
n |
= |
index of refraction, n = |
i
If the TEM field distribution in a coaxial line is examined, the vector E can be observed to be at any angle to the plane of incidence. This means that a TEM wave in a coaxial line is not uniform (unlike the same wave in free space or between plane conductors). However, because of the symmetry of the field distribution, it can be concluded that the electromagnetic field in the coaxial line consists of two equal parts: one in the perpendicular and the other in the parallel polarization. It is known from optics that there is one particular angle of incidence, referred to as Brewster's angle, which makes total refraction of the parallel-polarized signal to the second medium. In other words, if the dielectric is installed at Brewster's angle, the coefficient of reflection from the interface will be zero for all parallel-polarized signals. In the typical case for an air dielectric interface, Brewster's angle can easily be calculated as arctan
, where ε is the dielectric constant of the bead material. Figure 7 shows curves calculated from the theoretical reflection coefficient magnitudes of two cases: first for normal incidence, and second for oblique incidence at Brewster's angle. Fresnel's equations were used in these calculations. In the first case, the incidence angle is equal to zero and the effective reflection coefficient is a sum of the magnitude's parallel and perpendicular polarization's coefficients. In the second case, the angle of reflection is a Brewster angle and the perpendicular polarization coefficient is only calculated because the parallel one is automatically equal to zero. The curves show that for materials with dielectric constants between 2.0 and 3.5 the overall reflection is approximately the same for both cases. Those values of dielectric constants were picked because of the typical data for insulating materials used in the microwave applications. Note that the curves shown depict the theoretical maximum values of the reflection. The reflection can be partially or totally compensated. There are some important additional issues. It is not totally correct to apply laws of Optics to microwave transmission lines. The Brewster, Snellius and Fresnel equations are only applicable if the transverse dimensions of the transmission line are much larger than the wavelength, which is typically true in optics. A coaxial line with radial dimensions of a few wavelengths can be designed, but it is not practical because such a line will generate and transmit a huge number of higher modes.
|
|
Some designs use an oblique bead, which closes off the whole line.13 However, this is not always convenient. The power distribution is non-uniform in the coaxial line and most of the power is in the vicinity of the center conductor as mentioned previously. Because of this, it is possible to install only part of the dielectric in the vicinity of center conductor at Brewster's angle.
A NEW DESIGN
It can be seen from both issues above that the theoretical calculations could not predict the electromagnetic performance of the bead. An electromagnetic modeling and design of experiment process were initiated in order to guarantee a good electrical performance.
The bead with oblique incidence has some advantages. First of all, it can be designed without matched holes. The dust cannot be collected without these holes. Some microwave components have an optional dust washer. According to Anderson, et al.,11 the beads with axial holes should theoretically have very low reflection at high frequencies. However, those beads cannot have radial symmetry. The new bead can be totally symmetrical in the radial plane and thus will not excite the second mode resonance.
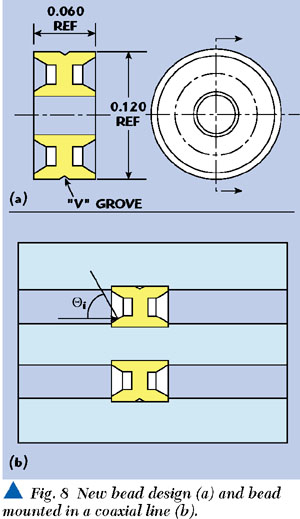
Figure 8 shows a drawing of the Ultem bead proposed for use in the 2.92 mm air-line K connector for frequencies up to 40 GHz and higher. In the middle of the bead, there is a line with low impedance, but other parts of the bead have high impedance. Both parts are designed to compensate each other. The bead could be designed with compensation at the same plane, but in this case it would have too complicated a shape. The edges of the bead have even higher impedance for fringing capacitance compensation. The faces have a special shape, which positions the dielectric at the angle of total refraction in the vicinity of both conductors. It is important to have Brewster's angle near the center conductor only, but the present shape is more convenient for manufacturing. The low impedance line has a low cut-off frequency, but its length is very short and it is much shorter than the limiting values.3 Also, the bead has total radial symmetry, and therefore cannot excite the second mode. Additionally, the V-groove increases the cut-off frequency.
|
|
The new bead can be either machined or molded. The new design was tested at the Astrolab Inc. facility in Warren, NJ, with 32022-2-29094K-36, Minibend K-12 cable assemblies and 2.9 to 2.4 mm adaptors (Astrolab part-number 29839). The current design passed a thermal shock test at 65° to +165°C. A typical test of the cable assembly's electrical performance is shown in Figure 9. The pair of adaptors is being tested under a mechanical durability test. It is mated and demated by wrenches, and every 50 connections the interface was gauged and the electrical performance was checked. At the release of this article, the pair passed 4750 connections without significant degradations.
|
|
ACKNOWLEDGMENTS
The author would like to thank John Zorzy from Gilbert Engineering, as well as his colleagues from Astrolab, Stephen Toma and Andrew Weirback. Ultem and Noryl are trademarks of General Electric Company. Rexolite is a trademark of Rex Corporation. Teflon is a trademark of Dupont. K connector is a trademark of the Anritsu-Wiltron Company. Minibend is a trademark of Astrolab Inc. *
References
1. John Zorzy, "18 GHz Mode-resonant-free Standard MIL-C-39012 TNC Connectors," Microwave Journal, Vol. 30, No. 5, May 1987, pp. 365370.
2. James Kubota, "TNC Connectors Meets New Performance Criteria," Microwaves, February 1981, pp. 7779.
3. H. Neubauer and F.R. Huber, "Higher Modes in Coaxial RF Lines," Microwave Journal, Vol. 12, No. 6, June 1969, pp. 5766.
4. John Gilmore, "TE11-mode Resonances in Precision Coaxial Connectors," General Radio Experimenter, Vol. 40, No. 8, August 1966, pp.1013.
5. Radiall, Catalog. See also US Patent 4,456,324.
6. Rudy Fuks, "Assessing Distortion at Microwave Interface Junctions," Microwaves & RF, August 1997, pp. 108116.
7. J. Flanagan, US Patent 4,718,864.
8. J Flanagan, et al., US Patent 4,867,703.
9. H. Bacher, et al., US Patent 5,269,702.
10. M. Ebisch, "Coaxial Measurement-line Inserts of High Precision for the Frequency Range 1-13 Gc," Frequenz, February 1959, Vol. 13, No. 2, pp. 5256.
11. W. Anderson, H.D. Chai and F.J. Tisher, "Theoretical Analysis of Coaxial Supports," Technical Report by The Ohio State University Research Foundation for Sandia Corporation, February 1962, Columbus, OH.
12. Peter Rizzi, Microwave Engineering Passive Circuits, Prentice Hall, 1988.
13. B.A. Dahlman, "Application of Brewster's Angle to the Design of Coaxial-line Components for Microwaves," RCA Rec., June 1954, Vol. 15, pp. 238251.
Rudy Fuks received his Dipl. Eng. degree in radio communication engineering from the Moscow Telecommunications Institute in 1973. He joined the Telecommunications Design and Development Bureau, Moscow, Russia, where he held positions as lead engineer, chief design engineer and department head. His main interest included design of passive microwave components, such as coaxial connectors and adaptors, terminations, detectors and antennas. In 1994 Fuks joined Astrolab Inc., Warren, NJ, as an RF design engineer, where he is responsible for the design of passive microwave components. Since 1998 he has been a principal RF design engineer and assistant engineering manager. Rudy Fuks can be reached by phone (732) 560-3800 or e-mail rfuks@astrolab.com