The diffusion capacitance/charge implementation is also based on the FBH model, as this model is intended for III-V HBTs, and considerable work has been done by its authors to accurately model HBT operation.7-8 In this case, the diffusion charge is associated mainly with the base-emitter junction and is given by:
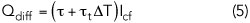
where τ is the time constant of base-emitter diffusion capacitance, τt is the temperature parameter of τ and Icf is the forward collector current. Although the temperature dependence is not very noticeable, the τt accounts for the temperature dependence of the base transit time.
The diffusion capacitance would normally apply to both the base-emitter and base-collector nodes. The reverse current is generally quite small (the base-collector junction is normally reverse biased), and most of the measurements were performed in the active region. It is not easy to extract this time constant for the base-collector diffusion charge, so an approximate value is used.
Thermal Network
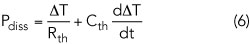
The self-heating is defined by the thermal RC network (see Figure 1). The transistor’s instantaneous dissipated power is used as the source for the thermal network. The RC network source and the temperature constitute a positive feedback. The phenomena can be expressed by the simulator to iterate a self-consistent solution. The equation is given as:
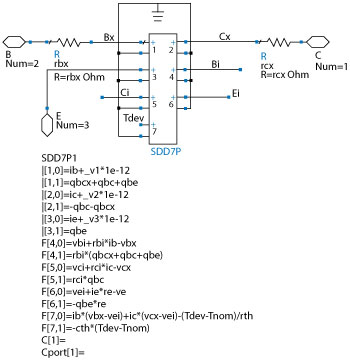
Figure 2 ADS SDD model of the HBT.
where ΔT= Tdev - Tnom, Tdev is the transistor internal temperature and Tnom is the room temperature. Cth and Rth are the thermal capacitance and resistance, respectively.
MODEL VERIFICATION
The large-signal model shown in Figure 1 with the modeling equations were constructed in the Keysight ADS simulator using an SDD (see Figure 2). The parameter extraction procedure starts with de-embedding the parasitic parameters, then extracts accessible resistances using fly-back measurements. The resistances are re-tuned to fit the S-parameters at cold-HBT conditions.9-10 The small-signal intrinsic equivalent circuit parameters are extracted using direct techniques without the optimization reported previously. Large-signal intrinsic circuit parameters are extracted from a large number of small-signal S-parameters with multi-bias points.
A 1 x 10 μm2 emitter InP HBT device was used to validate the model. DC, multi-bias, small-signal and large-signal microwave power characteristics were measured. The measured data was obtained on-wafer with an HP4145B semiconductor analyzer for DC, an HP8510C vector network analyzer for small-signal S-parameters from 0.5 to 40 GHz and a Focus microwave tuner at 15 GHz for source- and load-pull power measurements. The measurements were performed after the substrate was thinned to 100 μm, and the backside electroplated with gold.
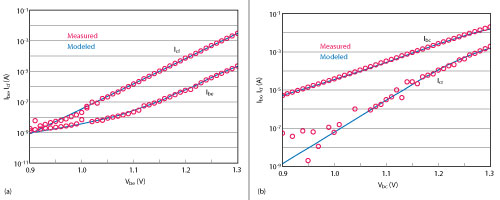
Figure 3 Measured vs. modeled Gummel plots: forward (a) and reverse (b).
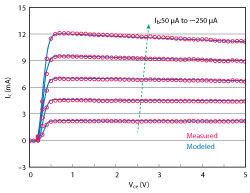
Figure 4 Measured vs. modeled Ic vs. Vce.
Figure 3a shows the forward Gummel plots simulated from the model and the measured characteristics. Reverse Gummel plots are shown in Figure 3b. Simulated and measured DC Ic-Vce characteristics under constant Ib bias conditions are shown in Figure 4. To demonstrate the validity of the model for small-signal microwave performance, the calculated S-parameters using the model are compared with the experimental results at two different bias points in Figure 5. Reasonably good agreement is shown between the simulated and measured S-parameters. Figure 6 shows measured and simulated large-signal microwave power characteristics at 15 GHz. Simulated data using the developed model agrees well with the measured data.
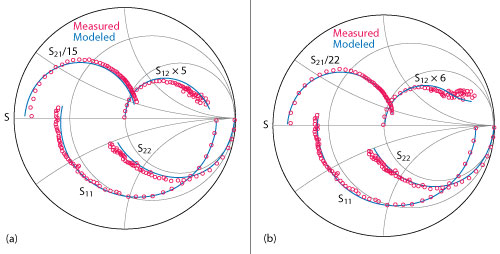
Figure 5 Measured vs. modeled S-parameters from 0.5 to 40 GHz for operating conditions of Ic = 9 mA, Vce = 3 V (a) and Ic = 4.4 mA, Vce = 3 V (b).
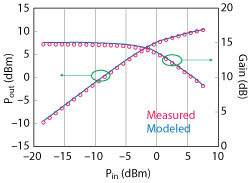
Figure 6 Measured vs. modeled gain and output power vs. input drive at 15 GHz, with the HBT biased at Ic = 9 mA and Vce = 3 V.
CONCLUSION
A new, large-signal InP HBT model that accounts for self-heating and soft-knee effects has been developed and implemented in ADS. The impact of the soft-knee effect is successfully modeled with a bias-dependent collector resistor, Rci, implemented as a function of three fit parameters and collector current. Good agreement between measurement and simulation using the developed model was achieved for DC, multi-bias small-signal and large-signal microwave power characteristics.
ACKNOWLEDGMENT
This work was supported by the Advance Research project of China and the Advance Research project of the People’s Liberation Army (PLA) in China.
References
- H. W. Liu and F. Tong, “Performance Improvement of Power Amplifiers Using an Asymmetrical Spurline Structure,” Microwave Journal, Vol. 53, No. 1, January 2010.
- W. L. Chen, X. Z. Liu, H. D. Wu and G. J. Wang, “A Wideband Chaotic Colpitts Oscillator with Negative Resistance Enhancement for UWB Applications,” Microwave Journal, Vol. 58, No. 9, September 2015, pp. 88–96.
- C. I. Lee, Y. T. Lin, B. R. Su and W. C. Lin, “SiGe HBT Large-Signal Table-Based Model with the Avalanche Breakdown Effect Considered,” IEEE Transactions on Electron Devices, Vol. 62, No. 1, January 2015, pp. 75–82.
- A. R. Testera, A. P. Perez, M. F. Barciela and P. J. Tasker, “Design of Injection-Locked Oscillator Circuits Using an HBT X-Parameters™-Based Model,” IET Microwaves, Antennas & Propagation, Vol. 9, No. 4, March 2015, pp. 380–388.
- B. R. Wier, K. Green, J. Kim, D. T. Zweidinger and J. D. Cressler, “A Physics-Based Circuit Aging Model for Mixed-Mode Degradation in SiGe HBTs,” IEEE Transactions on Electron Devices, Vol. 63, No. 8, June 2016, pp. 2987–2993.
- M. Rudolph, “Compact HBT Modeling: Status and Challenges,” IEEE MTT-S International Microwave Symposium Digest, May 2010, pp. 1206–1209.
- M. Rudolph and R. Doerner, “Consistent Modeling of Capacitances and Transit Times of GaAs-Based HBTs,” IEEE Transactions on Electron Devices, Vol. 52, No. 9, September 2005, pp. 1969–1975.
- M. Rudolph, R. Doerner, K. Beilenhoff and P. Heymann, “Scalable GaInP/GaAs HBT Large-Signal Model,” IEEE Transactions on Microwave Theory and Techniques, Vol. 48, No. 12, December 2000, pp. 2370–2376.
- Y. B. Sun, J. Fu and J. Yang, J. Xu, Y. Wang, J. Cui, W. Zhou, Z. Wei and Z. Liu, “An Improved Small-Signal Model for SiGe HBT Under Off-State, Derived from Distributed Network and Corresponding Model Parameter Extraction,” IEEE Transactions on Microwave Theory and Techniques, Vol. 63, No. 10, October 2015, pp. 3131–3141.
- T. K. Johansen, R. Leblanc, J. Poulain and V. Delmouly, “Direct Extraction of InP/GaAsSb/InP DHBT Equivalent-Circuit Elements from S-Parameters Measured at Cut-Off and Normal Bias Conditions,” IEEE Transactions on Microwave Theory and Techniques, Vol. 64, No. 1, January 2016, pp. 115–124.
