This article addresses the practical issues using high Q dielectric resonator (DR) cavity designs for RF/microwave oscillators. DR materials and basic cavity structures are described, along with the characterization and measurement of cavity Q. The complex resonant modes and coupling structures are detailed, with special emphasis on the impact of coupling and tuning structures on various resonant modes. Electromagnetic (EM) simulation and the equivalent circuit of the resonator that can be incorporated into linear and nonlinear circuit simulations are discussed and demonstrated.

Table 1

DR loaded cavities are important for RF/microwave filters and oscillators because of their high quality factor, Q and small size. They offer similar Q as the waveguide cavity in just an eighth to one twelfth the size. They provide excellent temperature stability when designed with a proper choice of dielectric material. However, the two common problems in dielectric resonator oscillator (DRO) design are degradation of the cavity Q from tuning and support structure and interference from higher order modes. Proper characterization of a DR loaded cavity can avoid these issues, allowing rapid prototyping with optimized DRO performance.

Related Resources

High Velocity Cable Assemblies: ACH Series
KYOCERA AVX WBR Series of Thin Film Wire Bond Resistors
18.0 - 40.0 GHz, 50-W Solid State Amp: AMP2145C-LC
MCV Microwave

Figure 1

Figure 1 Typical configuration of a dielectric loaded cavity.

The widespread use of ceramic DRs to replace metallic resonant cavities in RF and microwave circuits started in the 1970s, with the first low loss, temperature stable barium tetra-titanate ceramic materials.1-4 Further development of high dielectric constant ceramics with adjustable temperature coefficients enabled microwave engineers to use these materials in oscillator and narrowband filter designs for radar detectors, cellular phone and public safety base stations, satellite receivers and satellite broadcasting (TVRO/DBS).5-26

Table 2

Figure 2

Figure 2 Mode chart showing the four resonant modes of a DR cavity at 10 GHz (εr = 30 and Qf = 150,000).

DR CAVITY CHARACTERISTICS

The most direct way to reduce the cost of microwave circuits is to reduce their size. At a given frequency, the size of a DR is considerably smaller than that of an air resonant cavity, because the relative dielectric constant of the material is substantially larger than unity, which is the dielectric constant of air. Ideally, the size reduction equals the square root of the resonator’s dielectric constant, εr. Even though the dielectric resonator and its metal enclosure need to be separated by substantial distance, one can reasonably achieve volume miniaturization of 1/8 to 1/12 comparing a dielectric resonator to an air cavity with the same Q. Examples of commercially available high Q dielectric materials are shown in Table 1. In general, most dielectric materials can have their temperature coefficients adjusted, provided it does not affect the Q value. The product of dielectric Q and frequency (Qf) is pretty much a material constant in the usable frequency range.

A typical mechanical configuration of a DR loaded cavity is shown in Figure 1. It is well known in practical high Q DR cavity design that the ratio of cavity height (Cty_H) to dielectric resonator thickness (DR_t) should be around 3 and that of cavity diameter (Cty_D) to dielectric diameter (DR_OD) should be greater than 1.5. Also, two other parameters that are not as well published can affect the design drastically: the ratio between the dielectric resonator outer diameter (DR_OD) and thickness (DR_t), denoted as the aspect ratio, and the ratio between the dielectric resonator inner diameter (DR_ID) and outer diameter (DR_OD).

Table 3

The advantage of DR loaded cavities over rectangular waveguide and regular air cavities is depicted in Table 2. Typically, the size of the air cavity is fairly large and may be impractical for many applications below 3 GHz. A DR with a dielectric constant of 45 and a Qf of 45,000 offers approximately 92 percent volume reduction while still maintaining very high Q. In the frequency range of 5 to 10 GHz, a DR with a dielectric constant of 30 and a Qf of 150,000 achieves better cavity Q than the rectangular waveguide and 86 percent volume reduction. The advantage is obvious; however, DR loaded cavities present some challenges: spurious and quite complicated resonant modes.

Table 4

DR LOADED CAVITY MODES

The design of an RF/microwave oscillator using a DR loaded cavity must consider the cavity’s resonant frequency, coupling to the source and load and high order spurious resonant modes. Although there are closed approximate solutions to calculate these parameters and EM numerical analysis can compute the results, a systematic study has not been published. The mode-matching technique in EM simulation has been used to calculate the resonant frequency, cavity Q and coupling in the cavity for a DR loaded cavity. The recent progress of commercially available 3D EM simulator techniques, increased computation speed and affordable large capacity memory enable engineers to perform DR cavity simulation and design in a reasonable time.

Table 5

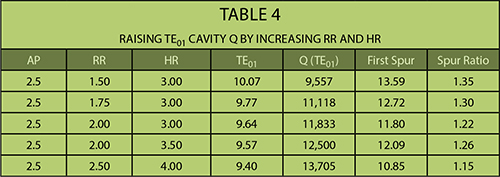
As an example, for a DR with εr =30, Figure 2 shows the HFSS computations for the various modes at 10 GHz, as the aspect ratio (denoted as AP) varies from 2.0 to 3.5. This is known as a mode chart. The numerical values are summarized in Table 3. Comparing the values in Table 3 and the unloaded Q of 15,000, the TE01 mode cavity retains around 60 to 70 percent of the Q (i.e., 1/tan(δ0l)) of the dielectric puck material. This is because the design employs the empirical rules that were noted earlier: 1) the ratio of the diameter of the metallic cavity to the outer diameter of the DR puck, denoted RR, is 1.5; and the ratio of the metallic cavity height to the thickness of the DR puck, denoted as HR, is 3. The Q of the TE01 mode cavity can be increased if larger RR and HR values are used, as shown in Table 4. However, while Q can be increased, the spurious ratio, defined as the ratio of the first higher mode frequency to the fundamental TE01 mode frequency, will become smaller, meaning the higher mode is closer in frequency.

Table 6

Table 5 shows the effects of an alumina (Al2O3) standoff and Rogers RO3010 PCB, where RR = 1.5 and the ratio of the DR outside diameter to the insider diameter (DR_OD/DR_ID) is 2.5. All the design variations seem to be quite acceptable, namely with 5 percent degradation of cavity Q and maintaining a spurious ratio of at least 1.23. However, a significant degradation in Q occurs if the DR puck is placed too close to the PCB. Tuning can be achieved using either a metal or dielectric disc. Table 6 compares the tuning as a function of the distance to the cover using a 0.5 mm tuning disk (the distance to the cover is normalized to the height of the DR). In general, for the same amount of frequency tuning, a metallic tuning disk can degrade the Q more than a dielectric tuning disk. The field distribution is important in designing the excitation and coupling of a resonant cavity. Typical E and H fields are shown in Figure 3.

Figure 3

Figure 3 Typical E and H fields of the TE01 mode resonator.

DRO TOPOLOGIES

Three topologies are used for DRO designs: one with the DRO in series feedback and two with the DRO in parallel feedback (see Figure 4). The DR is either one-port or two-port coupled to the active device in the DRO. A 3D view of a one-port coupled DR cavity is shown in Figure 5, where the arrow indicates the possible shifting of the excitation plane to that location.

Figure 4

Figure 4 DRO topologies: parallel feedback (a), parallel feedback (b), series feedback (c).

Three examples of DRO designs are presented, each with a different length of the coupled microstrip line in the cavity. These represent the ratio of the loaded to unloaded Q (QL/QO) of 2/3, 1/2 and 1/3 and a coupling resistance of 0.5, 1.0 and 2.0 with respect to the equivalent series resonator of the DR cavity (RO). Figure 6a shows the equivalent circuit of the one-port coupled DR cavity with an ideal transformer and phase shifter (using a section of transmission line) to match EM simulation and measured results. The coupling can be extracted from the ideal coupled resonator circuits in Figure 6b. The coupling coefficient (β) can be obtained from the maximum return loss (RLO), either from measurement (see Figure 6c) or simulation, as follows:

Figure 5

Figure 5 One-port coupled DR cavity.

Figure 6

Figure 6 Equivalent circuit of a one-port coupled DR cavity with ideal transformer and section of transmission line for shifting the phase (a) circuit for coupling and resonator QO extraction (b) and return loss measurement used to calculate the coupling coefficient (β).

Math 1

 

The Smith chart can be used to determine the case of under-coupled (β<1) or over-coupled (β>1). The following equations are used to obtain the unloaded Q (Q0):

Math 3

For the first design example, the under-coupled condition where the coupled resistance (RA) equals 0.5R0, two sets of simulation results are shown: one without shifting the excited reference plane (see Figure 7a), the other shifted to make it almost identical to the ideal equivalent circuit (see Figure 7b). Similarly, Figure 8 shows the critical-coupled condition, where RA equals R0; Figure 9 shows the over-coupled case, where RA equals to 2R0.

A two-port coupled DR cavity has the two ports arranged either on the same side of the cavity or facing opposite directions (see Figure 10). A coupled cavity should yield a QL/Q0 ratio between 0.5 and 0.66 to optimiz the phase noise of the oscillator. The corresponding transmission loss of a coupled DR cavity should range from 6.5 to 9.5 dB, according to:

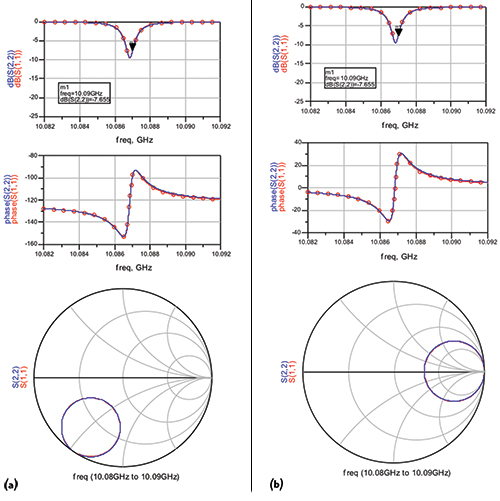
Figure 7

Figure 7 HFSS simulation and equivalent circuit of the under-coupled design with the excitation at the coaxial input plane (a) and the reference shifted 5.1 mm into the cavity (b).

Math 4

Most relevant works regard the two topologies in Figure 10 to be electrically identical. However, the equivalent network of Figure 10c fits the EM simulation of Figure 10a fairly well, while Figure 10b only fits Figure 10d well. The difference is the phase of S21. Figure 11 substantiates the equivalent circuits for the two-port topologies, showing the HFSS simulations for the respective circuits.

Figure 8

Figure 8 HFSS simulation and equivalent circuit for the critical-coupled design, with the excitation reference shifted to emulate an ideal series resonator.

Conclusion

This article addressed the issues of dielectric resonator loaded cavities in RF/microwave oscillator design, discussing DR characterization and modeling. The major characteristics of DR loaded cavities were analyzed, including cavity Q, resonant frequency, high order modes and coupling structures. Data obtained by 3D EM simulation should help designers achieve high Q in the cavity and avoid high order spurious modes that can interfere with the fundamental mode. Equivalent networks were presented that match the EM simulation results in the narrow band of the oscillator frequency. This research should help advance RF/microwave DRO design and development.

Figure 9

Figure 9 HFSS simulation and equivalent circuit for the over-coupled design, with the excitation reference shifted to emulate an ideal series resonator.

References

  1. J. K. Plourde, H. M. O’Bryan, Jr., D.F. Linn and H. J. Thomson, Jr., “Ba2Ti9O20 as a Microwave Dielectric Resonator,” Journal of the American Ceramic Society, Vol. 58, pp. 418–420, Sept.-Oct. 1975.
  2. D. J. Passeand and R. A. Pucel, “A Temperature-Stable Bandpass Filter Using Dielectric Resonators,” Proceeding of the IEEE, pp. 730, June 1972.
  3. K. Wakko, T. Nishikaw, S. Tarnura and Y. Ishikawa, “Microwave Bandpass Filters Containing Dielectric Resonators With Improved Temperature Stability and Spurious Response,” IEEE International Microwave Symposium Digest, pp. 63–65, 1975.
  4. J. K. Plourde and D. F. Linn, “Microwave Dielectric Resonator Filters Utilizing Ba2Ti9O20 Ceramics,” IEEE International Microwave Symposium Digest, pp. 290–293, 1977.
  5. Kajfez and P. Guillon, “Dielectric Resonators,” 2nd Edition, SciTech Publishing, 1998, ISBN 1-884932-05-3.
  6. J. K. Plourde and C. L. Ren, “Application of Dielectric Resonators in Microwave Components,” IEEE Trans. on Microwave Theory Tech., Vol. MTT-29, pp. 754, Aug. 1981.
  7. S. J. Fiedziuszko, “Dual-mode Dielectric Resonator Loaded Cavity Filters,” IEEE Trans. on Microwave Theory Tech., Vol. MTT-30, pp. 1311, Sep. 1982.
  8. Y. Kobayashi and M. Minegishi, “Precise Design of a Bandpass Filter Using High-Q Dielectric Resonators,” IEEE Trans. on Microwave Theory Tech., Vol. MTT-35, pp. 1156, Dec. 1987.
  9. S. W. Chen and K. A. Zaki, “Dielectric Ring Resonators Loaded in Waveguide and on Substrate,” IEEE Trans. on Microwave Theory Tech., Vol. MTT-39, pp. 2069, Dec. 1991.
  10. Xiang-Peng Liang and K. A. Zaki, “Modeling of Cylindrical Dielectric Resonators in Rectangular Waveguides and Cavities: IEEE on Microwave Theory and Tech., Vol. MTT-41, pp. 2174, Dec. 1993.
  11. Ji-Fuh Liang, K. A. Zaki and Ali E. Atia, “Mixed Modes Dielectric Resonator Filters,” IEEE Trans. on Microwave Theory Tech., Vol. MTT-42, pp. 2449, Dec. 1994.
  12. Ji-Fuh Liang and William D. Blair, “High- TE01 Mode DR Filters for PCS Wireless Base Stations,” IEEE Trans. on Microwave Theory Tech., Vol. 46, No. 12, December 1998.
  13. S. A. Vitusevich, K. Schieber, I. S. Ghosh, N. Klein and M. Spinnler, “Design and Characterization of an All-Cryogenic Low Phase-Noise Sapphire K-Band Oscillator for Satellite Communication,” IEEE Trans. Microw. Theory Tech., Vol. 51, No. 4, pp. 163–169, Jan. 2003.
  14. M. E. Tobar, D. Cros, P. Blondy and E. N. Ivanov, “Compact, High Q, Zero Temperature Coefficient, TE011 Sapphire-Rutile Microwave Distributed Bragg Reflector Resonators,” IEEE Trans. Ultrason., Ferroelectr. Freq. Control, Vol. 48, No. 3, pp. 821–829, May 2001.
  15. J. D. Anstie, J. G. Hartnett, M. E. Tobar, E. N. Ivanov and P. L. Stanwix, “Second Generation 50 K Dual-Mode Sapphire Oscillator,” IEEE Trans. Ultrason., Ferroelectr. Freq. Control, Vol. 53, No. 2, pp. 284–288, Feb. 2003.
  16. E. N. Ivanov and M. E. Tobar, “Low Phase-Noise Microwave Oscillators With Interferometrics Signal Processing,” IEEE Trans. Microw. Theory Tech., Vol. 54, No. 8, pp. 3284–3294, Aug. 2003.
  17. L. Zhou, Z. Wu, M. Sallin and J. K. A. Everard, “Broad Turning Ultra Low Phase Noise Dielectric Resonator Oscillators Using SiGe Amplifier and Ceramic-Based Resonators,” IET Microwave Antennas Propag., Vol. 1, No. 5, pp. 1064–1070, Oct. 2007.
  18. D. Y. Jung, K. C. Eun and C. S. Park, “High-Q Circular LTCC Resonator Using Zigzagged Via Posts and a λ/4 Short Stub for Millimeter Wave System on Package Applications,” IEEE Trans. Adv. Packag., Vol. 32, No. 1, pp. 216–222, Feb. 2009.
  19. L. Zhou, R. Chu, Z. Wu, W.Y. Yin and J. F. Mao, “Broad Tuning Low Noise Ku-Band Dielectric Resonator Oscillators,” Asia-Pacific Microwave Conf., Dec. 2008, pp. 1–4.
  20. P. Rice, M. Moor, A. R. Barnes, M. J. Uren, N. Malbert and N. Labat, “A 10 GHz Dielectric Resonator Oscillator Using GaN Technology,” IEEE MTT-S International Microwave Symposium Digest, Vol. 3. Jun. 2004, pp. 1497–1500.
  21. P. Stockwell, D. Green, C. Mcneilage and J. H. Searls, “ A Low Phase Noise 1.3 GHz Dielectric Resonator Oscillator,” IEEE Int. Freq. Control Symp., May 2006, pp. 882–885.
  22. A. Warburton, “A Phase Tuned, Fixed Frequency Dielectric Resonator Oscillator Design,” in Proc. Eur. Microw. Conf., Oct. 2005, pp. 1–4.
  23. C. Florian, P. A. Traverso, G. Vannini and F. Filicori, “Design of Low Phase Noise Dielectric Resonator Oscillators With GaInP HBT Devices Exploiting a Non-Linear Noise Model,” IEEE MTT-S International Microwave Symposium Digest, June 2007, pp. 1525–1528.
  24. J. F. Gravel and J. S. Wight, “On the Conception and Analysis of a 12 GHz Push-Push Phase Locked DRO,” IEEE Trans. Microwave Theory Tech., Vol. 54, No. 1, pp. 153–159, Jan. 2006.
  25. O. Llpois, G. Cibiel, Y. Kersale, M. Regis, M. Chaubet and V. Giordano, “Ultra Low Phase Noise Sappire-SiGe HBT Oscillator,” IEEE Microwave Wireless Compon. Lett., Vol. 12, No. 5, pp. 157–159, May 2002.
  26. K. Hosoya, K. Ohata, M. Funabashi, T. Inoue and M. Kuzuhara, “V-Band HJFET MMIC DROs With Low Phase Noise, High Power and Excellent Temperature Stability,” IEEE Trans. Microw. Theory Tech., Vol. 51, No. 11, pp. 2250–2258, Nov. 2003.

Figure 10

Figure 10 Two-port DR cavity with both ports on the same side of the cavity (a) and equivalent network (b). Two-port cavity with the ports on opposite sides (c) and equivalent network (d).

Figure 11

Figure 11 HFSS simulation for the two-port DR cavity with both ports on the same side, using the Figure 10b network (a). HFSS simulation for the two-port with ports on opposite sides, using the Figure 10d network (b).