
The electrical properties of a loss-less coupler, using TEM mode coupled lines, can be described in terms of even- (Zoe) and odd- (Zoo) mode impedances and its primary parameters [L] and [C] matrices2
where

Lo and Co are the proper inductance and capacitance of the isolated lines, respectively. M and γ are the mutual inductance and coupling capacitance of the coupled lines, respectively.

Various numerical techniques can be used to determine the accurate electromagnetic parameters of the coupled lines. However, they are too time-consuming for direct use in circuit design. Closed-form analytical models are highly desirable in circuit design. This article presents a set of rigorous expressions for the characteristic impedances, elements of the inductance and capacitance matrices for rectangular coaxial couplers with circular and square inner conductors having an outer to inner conductor ratio between 1.4 and 10 and a parameter u, related to the cut depth d, varying between 0 and 0.99. These expressions are deduced from analysis results of the structures by the finite element method (FEM) and the method of moment (MoM).1–3

Rectangular Coaxial Couplers with Circular and Square Inner Conductors
The cross-sections of rectangular coaxial couplers with circular and square inner conductors are shown in Figures 1 and 2, respectively. Each coaxial line is assumed to be lossless, with an inner conductor of radius rc or side 2a, and an outer rectangular conductor of height h and width W = 2D. The coaxial lines are filled with a material with a dielectric constant ερ. A portion of each cable is cut out and two of these cut cables are joined to form the coupled line. The cut depth is shown as d on the cross-section and


where

Rectangular Coaxial Couplers with Circular Inner Conductors
Numerical Results
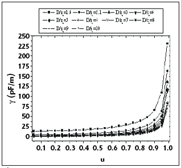
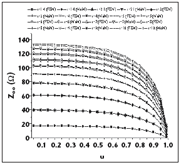
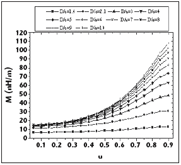
The numerical results for the electromagnetic parameters (Zoe, Zoo, [L] and [C]) of the rectangular coaxial couplers with circular inner conductors are shown in Figures 3 to 8. The impedance results obtained demonstrate the excellent coherence between the FEM and MoM methods.

Derivation of Analytical expressions
Characteristic Impedances
Equation 3 expresses the even-mode characteristic impedance (Zoe) of the coupled lines
![]()
where


Equation 4 gives the odd-mode characteristic impedance (Zoo) of the coupled line

where


Inductance Per Unit Length Matrix
Equations 5 and 6 give the proper and the mutual inductances of the rectangular coaxial coupler with circular inner conductors, respectively

Capacitance Per Unit Length Matrix
Equations 7 and 8 give the proper and coupling capacitances of the rectangular coaxial coupler with circular inner conductors, respectively


Table 1 shows a comparison between the analytical and numerical results. The relative errors between the numerical and analytical results are less than 2 percent over a wide range, indicating the good accuracy of the closed-form expressions for rectangular coaxial couplers with circular inner conductors.
Rectangular Coaxial Couplers with Square Inner Conductors

Numerical Results
Figures 9 and 10 show the characteristic impedances of the rectangular coaxial couplers with square inner conductors, calculated using the coherent methods (FEM and MoM).
The numerical results for the elements of the [L] and [C] matrices, for different values of outer to inner conductors ratios, are shown in Figures 11 to 14.
Derivation of Analytical Expressions
Characteristic Impedances
For this type of coupler, the even-mode characteristic impedance (Zoe) can be expressed by
![]()
where


Equation 10 gives the odd-mode characteristic impedance (Zoo)

Inductance Per Unit Length Matrix
Equations 11 and 12 give the proper and the mutual inductances of the rectangular coaxial coupler with square inner conductors


Capacitance Per Unit Length Matrix
Finally, Equations 13 and 14 give the proper and the coupling capacitance of the rectangular coaxial coupler with square inner conductors


A comparison between the analytical and the numerical results is given in Table 2, showing the good accuracy of the closed-form expressions for the rectangular coaxial couplers with square inner conductors.
Conclusion
This article presents a set of accurate, closed-form formulas for the primary parameters (inductance [L] and capacitance [C] matrices) and the impedances (Zoe, Zoo) of the even- and odd-modes for rectangular coaxial couplers with circular and square inner conductors. These expressions, deduced from analysis results by the finite element method and the method of moment, are valid in a wide range of outer to inner conductor ratios.
References

1. N. Benahmed, M. Feham and M. Kameche, “Finite Element Analysis of Planar Couplers,” Applied Microwave & Wireless, Vol. 12, No. 10, October 2000.
2. N. Benahmed and M. Feham, “Finite Element Analysis of RF Couplers with Sliced Coaxial Cable,” Microwave Journal, Vol. 43, No. 11, November 2000, pp. 106–120.
3. A.R. Djordjevic, D. Darco, M.C. Goran and T.K. Sarkan, Circuit Analysis Models for Multiconductor Transmission Lines, Artech House Inc., Norwood, MA, 1997.
Nasreddine Benahmed received his DSc degree from the University of Tlemcen, Algeria, in 2002. He has been a professor of communication systems since 2003. His current interests include RF and microwave transmission lines.
Salima Seghier is working on her MS degree in electronics, specializing in microwave and telecommunication systems at the University of Saida, Algeria. She is presently working as a communications engineer.
