Polarization is a basic consideration in the design of any wireless communication system. Most systems use either linear or circular polarization. For a simple description of these two types of wave polarization, consider the illustration shown in Figure 1. This figure shows an electromagnetic wave approaching an observer. This observer has the capability to monitor the orientation of the wave’s electric field vector over time. If the tip of the vector always lies within the same 2-D plane (blue trace), the wave is linearly polarized (LP). If, on the other hand, the tip of the vector rotates in a circle as time progresses and the frequency of the rotation is equal to the frequency of the wave (green trace), the antenna is circularly polarized (CP). An alternative way to visualize circular polarization is to regard a CP wave as the superposition of two LP waves that lie in mutually orthogonal planes and are 90° out of phase with each other.
 | ||
| Fig. 1 An electromagnetic wave approaching an observer. | ||
In the absence of reflections and multipath effects, LP antennas radiate LP signals and CP antennas radiate CP signals. In general, LP antennas have reduced design constraints in comparison to CP antennas and are therefore much more commonly used. At microwave frequencies, CP antennas find use primarily in satellite communications. Other applications also make use of CP antennas in situations where precise alignment between transmit and receive antennas is impractical, or where the polarization of the transmitted signal is unknown. It is interesting to note that, for wireless communications, CP antennas have additional advantages over LP signals in certain multipath fading environments. For example, when LP signals hit a metal surface, the incident and reflected waves tend to cancel each other out. However, with CP signals, wave cancellation does not occur since the incident and reflected waves have a different sense of rotation.1
Several methods exist for measuring CP antenna patterns.2,3 One method is to measure the pattern of the antenna under test (AUT) with another CP antenna. The only disadvantage of this approach is the difficulty in designing microwave CP antennas that can maintain high cross-polarization suppression over a wide frequency range. Using such antennas as measurement standards outside their range of polarization purity results in measurement errors.4 Another common approach is to use a rotating LP antenna as the measurement standard. If the rotation rate is much greater than the angular velocity of the pattern cut, the measured pattern simultaneously displays both the axial ratio and the beam pattern. The resulting graph is called a spinning linear pattern.
The phase-amplitude method for measuring CP radiation patterns is a procedure gaining increased popularity in the present era of computer-automated antenna measurement. This approach is also called the linear component method.2 The method typically uses a linearly-polarized standard gain antenna (SGA) to measure both the amplitude and phase across one or more cuts of a CP radiation pattern. The measured data is stored electronically and then post-processed in order to reconstruct the CP co- and cross-polarization patterns. The following two sections describe an automated antenna measurement system with the capability to measure both the amplitude and phase of an antenna’s radiation pattern and how to use this measurement setup to measure the radiation pattern of a CP antenna.
Automated Test Setup
The automated antenna measurement system at Texas A&M is shown in Figure 2. It consists of the following primary elements:
- Azimuth positioner
- FR8502 positioner controller
- AL-4146-2 power control unit
- Agilent 8510C network analyzer
- HP 8341B RF synthesizer
- HP 83622A LO synthesizer
- HP 85309 LO/IF unit
- HP 85320A/85320B test/reference mixers
- FR959 automated antenna measurement workstation
 | ||
| Fig. 2 The antenna measurement system. | ||
For frequencies above 20 GHz, the test setup can be modified to allow automated operation up through 40 GHz by connecting an HP 83554A frequency multiplier to the RF synthesizer and by replacing the reference/test mixers with millimeter-wave equivalents.
The data acquisition workstation includes an IEEE card for interface with the positioner controller and network analyzer, as well as an I/O card for high speed collection of BCD format position transducer data. The positioning axis is driven by a servo-controlled DC motor, and utilizes tachometer feedback for precision control.
The FR959 Automated Antenna Measurement Windows 2000/XP-based software provides fully automated control of the data acquisition process, including control of the azimuth orientation of the antenna under test. Multi-frequency data acquisition for both source polarizations allow for complete characterization of the CP antenna under test. Data acquisition time is optimized through the feature of the software that allows for test sweeps to be timed in advance of the acquisition, which allows for the optimum velocity of the axis to be pre-determined. Variable data density is supported over the complete range of angles for each segment of a scan.
The amplitude and phase measurements required for the CP calculations are enabled through the use of a ratio measurement in the network analyzer, which is formed as the ratio of the received signal of the AUT to a reference signal generated within the RF subsystem. Measurements of the antenna under test for vertical and horizontal incident polarizations are currently obtained serially, but can be acquired during a single test by use of a polarization axis as part of a multi-axis raster scan, or by real-time transmit polarization switching. Precision data acquisition angle triggering assures that the two components for the CP calculation are collected at the same angle within a user defined error tolerance. Also, the amplitude and phase accuracy of the network analyzer are 0.03 dB and 0.2° at a signal level 40 dB down from the reference signal level, which translates to an error of 0.04 dB in the subsequent calculation of the axial ratio of the antenna under test.
Measurement Procedure
The preceding section discussed the configuration of an automated antenna range capable of measuring both the amplitude and phase of an antenna’s radiation pattern. This section describes how to use such a setup to measure the radiation pattern of a CP antenna. As an introduction to the topic, however, it is appropriate to briefly outline the conventional procedure for measuring an LP antenna. Figure 3 illustrates the coordinate conventions that can be used for measuring any general LP antenna situated in the y-z plane with its electric field vector polarized along z. In this illustration, the antenna’s main beam angle happens to radiate in the direction (θ = 90°, φ = –15°). The E-plane co-polarization, Eθ(θ, φ = –15°), is measured by recording the variation in received power at the AUT as a z-polarized SGA transmitter sweeps across a desired range of angles θ in the φ = –15° plane. That same measurement is then repeated with a y-polarized SGA transmitter to obtain the E-plane cross-polarization, Eφ(θ, φ = –15°). Measuring the H-plane co- and cross-polarization, Eφ(θ = 90°, φ) and Eθ(θ = 90°, φ), follows an identical procedure, except that the radiation pattern is sampled in the θ = 0° plane across a desired range of angles φ.
 | ||
| Fig. 3 Coordinate conventions for an antenna linearly polarized along the Z axis. | ||
For CP antennas, the term principal plane can be defined simply as any slice or cut of the radiation pattern that passes through the peak of the main beam. As many or as few principal plane cuts as desired may be used to characterize the true 3-D radiation pattern. In fact, for a CP antenna with complete circular symmetry, such as the CP horn shown in Figure 4, just one principal plane cut may be sufficient to describe the entire CP radiation pattern.
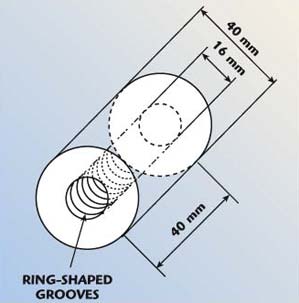 | ||
| Fig. 4 Sketch of a Ka-band CP corrugated horn. | ||
The phase-amplitude method modifies the conventional procedure for measuring an LP antenna to allow the measurement of a CP radiation pattern. The first step in the procedure is to measure the received amplitude and phase at the AUT as the linearly-polarized SGA transmitter sweeps across a desired range of angles ψ in a principal plane of the AUT. Next, the SGA is rotated 90° and the measurement is repeated across the same range of angles y for the same principle plane cut. The resulting sets of complex data can be designated as Eθ(ψ) and Eφ(ψ) since they represent orthogonal LP patterns taken across an identical cut of the AUT’s CP radiation pattern.
Once the measured data for Eθ(ψ) and Eφ(ψ) are stored electronically, they can be post-processed to reconstruct the co- and cross-polarized components of the CP radiation pattern across that same principal plane cut. At each angle of measurement, the right-hand CP (RHCP) component is given by
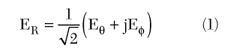
and the left-hand CP (LHCP) component by
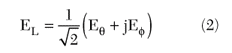
Depending on the design of the AUT, either ER(ψ) or EL(?) is the co-polarization pattern, with the other component representing the cross-polarization pattern. If |ER|>|EL| at the main beam angle, the AUT is right-handed and ER(ψ) is the co-polarization pattern. Otherwise, the antenna is left-handed and EL(ψ) is the co-polarization pattern.
To demonstrate this measurement technique, the test setup described in the preceding section is used to measure the radiation pattern of the CP horn shown previously. The results at 32 GHz are shown in Figure 5 for the linearly polarized fields; the resulting CP co- and cross-polarization patterns are shown in Figure 6. The CP co-polarization pattern is plotted versus frequency for the entire Ka-band in Appendix A, with minimum cross-polarization at 32 GHz.
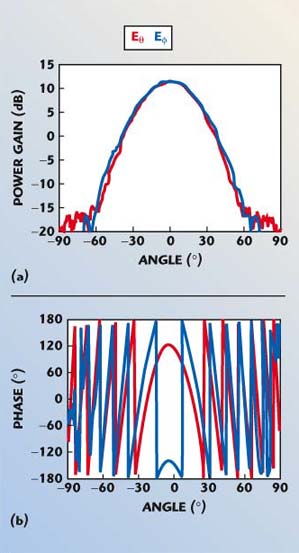 | ||
| Fig. 5 The phase-amplitude method applied to the CP horn; (a) linearly-polarized amplitude and (b) phase pattern. | ||
 | ||
| Fig. 6 Resulting CP co- and cross-polarization patterns. | ||
CALCULATING THE AXIAL RATIO
The polarization purity of a CP antenna is frequently described by specifying its axial ratio (AR). The axial ratio varies from 1 for an ideal CP antenna to ∞ for an ideal LP antenna. Having the capability to measure a CP antenna’s co- and cross-polarization pattern makes it possible to calculate this parameter exactly, without the need for additional measurement. Given an antenna’s CP co- and cross-polarization patterns, the axial ratio (AR) can be determined for any given angle in space using2
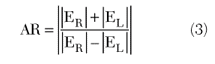
There is a common misconception that an antenna’s axial ratio can be computed simply as a ratio of any two orthogonal LP components — that is, as

or as
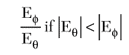
In reality, axial ratio depends on both the magnitude and phase of Eθ and Eφ. For example, suppose that the ratio of Eθ and Eφ is given by
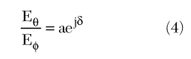
where a is a real number. The axial ratio may then be expressed as

where

which clearly includes both magnitude and phase information. Only if δ = 90° does the axial ratio equal a. For example, the ratio of the orthogonally polarized LP components shown for the CP horn is 1.015ej1.489 at the angle of maximum radiation (0.13 dB amplitude difference and 85° phase difference), corresponding to a measured axial ratio of 0.72 dB.
An advantage of the phase-amplitude method is that the axial ratio can be directly calculated using the equations presented in this section. Some antenna ranges, however, are much more sensitive to phase errors than to amplitude errors. Others have neither the capability to measure received amplitude and phase at the AUT nor the equipment necessary to take a spinning linear pattern. In those cases, it may be preferable to express the axial ratio as a ratio of orthogonal LP components, provided that one of the two orthogonal components is chosen to maximize (or minimize) the received power at the AUT.
Conclusion
This article has described a practical and accurate method for measuring CP antennas. The method is particularly well suited for implementation in automated antenna measurement systems that have the capability to measure both the amplitude and the phase of an antenna’s radiation patterns. An outline of a typical measurement setup and methodology was provided, along with a demonstration of the technique on a Ka-band CP antenna. Equations for calculating the axial ratio using measured phase and amplitude data have also been presented.
Acknowledgment
The authors wish to thank Dr. Berndie Strassner of Sandia National Laboratories for helpful technical discussions. They would also like to thank Dr. John Huang of the NASA Jet Propulsion Laboratory for lending them a Ka-band CP horn.
References
- J.H. Reisert, “Antenna Polarization Application Note,” Astron Wireless Technologies Inc., 2002.
- D. Kraus, Antennas, McGraw-Hill, New York, NY, 1950, pp. 444–486.
- IEEE Standard Test Procedures for Antennas, ANSI/IEEE Std. 149-1979, published by IEEE Inc., distributed by John Wiley & Sons Inc., New York, NY, 1979.
- T. Milligan, “Polarization Loss in a Link Budget when Using Measured Circular-polarization Gains of Antennas,” IEEE Antennas and Propagation Magazine, Vol. 38, No. 1, February 1996, pp. 56–58.
- K. Chang, I. Bahl and V. Nair, RF and Microwave Circuit and Component Design for Wireless Systems, John Wiley & Sons Inc., New York, NY, 2002, p. 482.
-

