The development of coaxial microwave components capable of handling high peak power without the presence of multipactor is an important part of component design for space and vacuum environments. Multipactor is a resonance type of discharge that can occur under vacuum conditions.1 The electric component of the electromagnetic field can have sufficient energy to cause the emission of electrons from the material surface. In a vacuum environment, the electron free path distance is greater than the electrode separation distance. This change in the distance relationship allows free electrons to impact the electrode surface. These collisions create a secondary electron emission from the electrode structure. The synchronization between the secondary electron emissions and the frequency of the electric field alternating polarity will accelerate the electrons back to the source electrode (see Figure 1). Under the appropriate conditions, the number of electrons will increase exponentially up to a saturation point, at which the electron density is large enough to block the electric field. This electron charge build up can cause a resonance type of breakdown in the form of a multipaction discharge.1 Multipaction discharge itself can also cause an additional saturation mechanism through its interaction with the electrodes.2
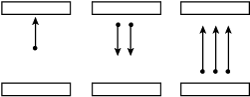
Figure 1 Multipactor between two planes.
There are two main conditions that must be present for multipactor. First, the one way transit time between the two electrodes is an odd number of half cycles N, where N is an odd positive integer (N = 1, 3, 5 …). Second, the secondary electron emission coefficient of the impact surface must exceed unity.
The multipaction discharge phenomenon is not always undesirable. In the 1930s, American Philo Farnsworth designed an amplifier vacuum tube for television signal transmission, based on the multipactor. This tube was later superseded by Zworykin’s Iconoscope.1 However, Farnsworth first derived the name multipactor from “AC Electron Multiplier,”2 originally describing hardware rather than the mode of the electron emission itself. Over time, in most space and vacuum applications, the term has come to define the harmonic electron breakdown.
Multipactor creates a sheet like cloud of electrons, which are oscillating between the two electrode surfaces.1 The discharge will heat the surfaces of the electrodes, increase signal noise, block the electric field and appear as a brief electron current between the two electrodes. In the case of a high mode (N mode) multipactor, several electron cloud sheets (exactly 2N-1) will oscillate between the surfaces under steady state conditions. Additionally, in some high power tubes, multipactor can emit visible light and X-rays. Single surface multipaction discharge can also occur on dielectric component surfaces, if there is a bias DC field, electric or magnetic, and a high frequency electric field is present parallel to the dielectric surface. This single surface discharge phenomenon on the dielectric surface is not applicable for coaxial lines. For further reading on the history of multipaction discharge analysis, current theory and practical information, see the works of Vaughan,1 Kishek2 and Ming Yu.3
The focus of Vaughan’s work with multipactor was in the field of high and very high power microwave tubes.1 Vaughan noted that multipactor is essentially a medium power phenomenon.1 The reason for this statement is that under very high energy, multipactor is not possible. The impact velocity of the emitted electron is of such a magnitude that it penetrates too deep inside the second electrode to cause secondary electron emission from its surface. This type of impact does not meet the second required condition for multipactor, since the secondary electron emission coefficient is less than one.
With regard to coaxial cables and connectors, Vaughan’s statement that multipactor as “essentially a medium power phenomenon” is not true in the majority of the cases. Coaxial cables and connectors, inherently, have a limited power handling relative to microwave tubes. In most cases, multipactor in a coaxial line is a high power phenomenon in that it occurs at a power level near the maximum capacity of the component. In fact, the multipaction discharge within a coaxial line is usually not catastrophic in and of itself. However, the discharge can vaporize some of the dielectric material within the coaxial line and create ionized gas particles. If the coaxial line is not properly vented, these collected gas particles can initiate an ionization breakdown within the structure. The ionization breakdown is typically the destructive failure mode.
Extensive research of the multipactor phenomenon has been performed in recent years. The European Space Agency (ESA) has hosted several multipactor workshops for space applications. There are also multiple options for multipactor calculations from Jet Propulsion Laboratories4 and ESA.5 However, most of the references describe multipactor in the applications of high power microwave tubes, plasma physics and particle acceleration. Many papers have been published with analysis and applications, yet there are few practical papers that reveal any guidance in designing coaxial components for space applications, where multipactor is a serious concern.
Most early references analyzed the simplest case, that being multipactor between two parallel plates. This application has a uniform field. Coaxial line analysis is much more complicated, because the field is not uniform. However, an examination of two parallel plates is necessary to establish the fundamental factors, which will later be analyzed in the frame of a coaxial system. For further reading on the multipactor analytical study under simplified conditions see the work of Udiljak, et al.7
According to Udiljak,6 the resonance condition for an applied electric harmonic field between two plates is:
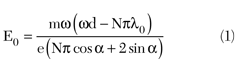
where m is the mass of an electron (9.1 × 10-31 kg), e is the electron charge (1.6 × 10-19 C), d is the distance between the plates, ω = 2πƒ and ωt = Nπ + α.
It is possible to calculate the multipactor zones from Equation 1. The multipactor zones are usually depicted in charts, which show the relationship of power (or voltage) versus the frequency-distance product. However, this analysis was done with respect to the electric field only, in the simplified conditions. This is in accordance with most references, which have removed the magnetic field influence because it is assumed to be negligible.
However, according to the Ampere-Maxwell law, the electric field will produce a circulating magnetic field. In a coaxial structure, the magnetic field lines are in concentric circular sweeps around the center conductor circumference.
The force that describes the electron movement under the influence of both electric and magnetic fields, named the Lorentz Force F, is defined as:

where q is the electron charge, E is the electric field, V is the electron velocity and B is the magnetic field induction. This equation shows that the magnetic field deflects the electron movement from a straight path. This deflection can be important.
At first look, the influence of the magnetic force does indeed look negligible. However, consider a special case. Suppose the first electron is displaced a very small distance in the axial direction. Under multipaction discharge conditions, when secondary electrons are released in a coaxial line, the fields are reversed. However, the vector product V × B will remain in the same direction because the velocity vector V has also changed direction. This means that the secondary electrons will be displaced in the same axial direction over an additional short distance. As the multipactor increases the rate of electron discharge, the space charge axial displacement caused by the cross product of vectors V and B will grow as well. The axial displacement in the coaxial line will move in the same direction as the incident wave because vectors V and E are in the same direction, which means that the vector product V × B is in the same direction as the Poynting vector. Since the typical frequency for a space application is in the gigahertz range, the axial displacement is going to be comparable to the radial gap in a very short time. Modifying Equation 2 and substituting B = μH (for vacuum μ = μ0) and H = E/Z0, Equation 2 can be modified as:

Equation 3 shows that the axial displacement is related to the radial acceleration by the factor Vμ0/Z0. The ratio μ0/Z0 (3.33 × 10-9) is a very small value. However, at microwave frequencies, there will be billions of such cycles per second. Additionally, the electron velocity V will increase at the end of each cycle. The influence of the electron velocity can be more simply shown through the analysis of the two plane multipactor rather than the more complicated structure and field distribution of a coaxial line. According to Vaughan,1 the electron impact velocity Vi is:

where ω = 2πf and V0 is the initial velocity. The multipaction discharge condition is present when ωt = Nπ + α, where α is the initial phase. In the simplest case, for a first order multipactor with zero initial velocity (N = 1, V0 = 0, and α is an integer number of π), Equation 4 can be rewritten as:

Equation 5 presents a very simplified model because, first, the use of a two plane first order multipactor, and second, according to Vaughan, the value of V0 is unknown because “it is a statistical distribution rather than a single variable value.”1 There are some differences in correlating the phase relations from a two plane structure to that of a coaxial line. Udiljak6 points out that in a coaxial line, the transmission time is normally longer for electrons emitted from the outer conductor than for electrons emitted from the inner conductor. This means that the phase relations in a coaxial line are less favorable for multipactor, when compared to the simplified model of two planes.
However, Equation 5 shows that, in each cycle, the electron velocity is growing from zero to a very large value because it is linearly proportional to the frequency. The proportional relationship of the impact velocity of the electron to frequency is evident from the fact that, as the frequency increases, the electron velocity must be significantly higher in order to reach the opposite electrode before the polarity reverses. This means that the axial displacement caused by the magnetic field is in fact not negligible and can have substantial effects, particularly at microwave frequencies. From this, it is evident that the velocity dependence on frequency makes the electron axial displacement to increase nonlinearly, as the frequency increases.
From plasma physics, the nonlinear force that a charged particle experiences in an inhomogeneous oscillating electromagnetic field is known as the Ponderomotive or Miller force. The Ponderomotive force influences the particle to drift toward the weak field area. This force is particularly important in the coaxial line because of the inhomogeneous field, which is stronger in the region of the center conductor. However, the axial displacement is different from that of the Ponderomotive force, which depends solely upon the electric field and has a radial influence on the electron position in a coaxial line.
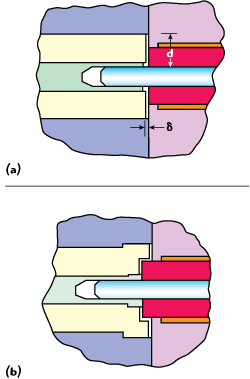
Figure 2 Cable-connector junction: (a) simplified connector and (b) practical design for high voltage handling.
One could say that the axial displacement is not important and that it may have no influence on multipaction. However, as noted before, most references contain data regarding multipactor between two planes. Usually, only a coaxial airline structure is discussed. The airline, however, has little practical interest. Most coaxial transmission lines, particularly for space applications, are fully or partially loaded by a dielectric material. In this case, the axial displacement has a large influence for a partially filled line, which is typical for any cable connector junction. Figure 2 shows a simplified coaxial cable-connector junction that is widely used for high frequency applications. One can see the air gap with height d and width δ. This air gap is a short line of high impedance that improves the electrical match between the cable and connector coaxial line sizes. Typically this air gap is the most susceptible part of the cable assembly to a multipactor event.
According to Udiljak,6 the rate of electron build up Ne(t) is determined by the following equation:

where Ne(0) is the initial electron quantity and σse is the secondary electron emission yield. For example, an electron cloud growing from 1 to 1014 takes 20 ns at 2 GHz, when the secondary electron emission yield σse = 1.5. This is close to the same time relationship as shown by Vaughan.1 This means that electrons can hit the electrode a few dozen times and the overall axial displacement is microscopic, because of the ratio of μ0/Z0 = 3.33 × 10-9 in Equation 3. However, the velocity can reach a significant value, particularly at a high frequency (see Equation 5). Therefore, the multipacting electrons will be displaced in an axial direction to a distance almost equivalent to that between the electrodes (d) in a very short amount of time. However, the electron cloud will hit the dielectric wall under a much smaller displacement (see distance δ) than the distance between electrodes (d).
In most practical cases, the gap width is at least ten times less than the height (d). Apparently, from the moment that the electrons hit the dielectric surface, the phase conditions for multipaction will be violated despite the fact that oblique incidence will increase the secondary emission. The presence of the dielectric wall inhibits the electron build up. This means that multipaction is small or may not exist. The properties of the dielectric barrier can be extended to other dielectric loaded interfaces, for example the junction of two SMA interfaces. Note that the single surface multipactor will have much greater axial displacement because the electron cloud will grow at a much slower rate.
Also note that, statistically, the electron can be located in any spot along the distance δ. This shows that the typical axial displacement required to hit the dielectric surface can be much smaller than δ. Some references6-8 point out that there are two different types of multipactor in coaxial lines: a two sided discharge between inner and outer conductor and the one sided discharge on the outer conductor only. The main reason for the single surface multipactor is the decreasing electron velocity due to the Ponderomotive force. Therefore, the electron is reversed back before reaching the center conductor. The single-sided multipactor can be present in high impedance lines only. It should be noted that the single surface multipaction was not yet confirmed by experiments as of 2007.
A practical design for high voltage handling is also shown in the figure. Here, the two dielectrics overlap each other, thereby increasing the voltage handling. However, if the overlap is too large, it can compromise the electrical match particularly at high frequencies. Theoretically, multipactor can happen between metal and dielectric surfaces in the gap area. However, the conclusion is the same: the narrower the gap is, the more it will suppress multipactor. According to some space equipment manufacturers, the main danger for such junctions is not multipaction itself, but rather trapped air that can easily create the conditions necessary for ionization breakdown. This breakdown can happen under relatively low power. From Paschen’s Law,12 for every pressure, there is a gap with a low breakdown point. Therefore, it is extremely important to design the connector to provide for positive venting of the junction.
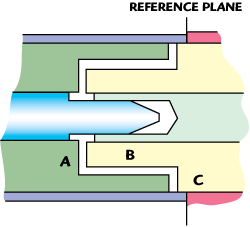
Figure 3 TNC interface junction.
Typical coaxial connectors for high power space applications have a dielectric loaded interface with overlapping surfaces. There are several coaxial connectors that have been specifically designed for space power applications, but they do not comply with the industry connector interface standard MIL-STD-348.13 The most common, industry standard, coaxial connector interface, for space power applications, is the TNC. The mated TNC connector interface is shown in Figure 3.
One can see that the TNC interface has an overlapped dielectric. There is no line of sight between the inner and outer conductors. There are three main regions, in the connector interface A, B and C, where multipactor can occur. Theoretically, multipactor can occur in region A, between the center conductor and dielectric. However, total breakdown of the TNC line appears to be impossible, because the TEM mode has no axial electric field. Thus, nothing can accelerate electrons in an axial direction within region B. As shown earlier, the Lorentz force equation (Equation 2) reveals that the electron will be deflected in the axial direction. With this knowledge, the TNC interface junction can be evaluated in the same manner as the practical cable-connector junction for high voltage handling. Apparently, if the air gap between mating dielectrics is narrow, it will suppress multipactor in region A because it inhibits electron acceleration. According to some space equipment manufacturers, the TNC interface is highly resistive to multipactor and in many cases it is impossible to initiate a multipactor event under extremely high power levels.
There are two main references for multipaction calculation: the Woo report and the ESA calculator. The R. Woo4 report was published in 1967 and is based on JPL NASA experimental data. Another option is the ESA calculator. The ESA calculator was released more recently and is much more convenient to operate. It can be downloaded for free from the ESA website (http://multipactor.esa.int/downloads.html). Particularly impressive are the options available to calculate multipaction for multicarrier signals. The ESA calculator also has the ability to calculate the multipaction handling for standard coaxial connector interfaces. However, when using the ESA calculator, there are some points that must be considered, when evaluating its outputs. It is surprising to find that the calculator gives the same outputs for a TNC connector as for N and 7 mm connectors. The N and 7 mm are both based on a 7 mm air line and both should have the same multipactor outputs. However, the TNC interface is based on an overlapped dielectric and it typically can handle much more power. For example, see the comparison in Rosario, et al.9 Additionally, there is only a single SMA connector option within the ESA calculator. The available connector is specified with a nominal gap of 0.99 mm, which is equivalent to the thick wall SMA plug interface per MIL-STD-348, Figure 310-3.13 However, this design is not representative of all SMA connectors available. Many SMA plug connectors are designed with a nominal gap of 1.25 mm, which is equivalent to the SMA plug interface per MIL-STD-348, Figure 310-1. This difference should be taken into account when considering the use of an SMA connector in space power applications.
Special attention needs to be given to the determination of an adequate safety margin. ESA recommends a multipaction safety margin of 3 to 4 dB by test and 8 to 12 dB by analysis. An additional safety margin is required for unmatched transmission lines.11 As was noticed by Ming Yu,3 the Woo report4 gives outputs in root mean square (RMS) voltage values, whereas the curves from the ESA calculator5 gives the output peak voltage. The primary difference between these outputs is that the RMS value already contains a 3 dB margin.
A final and very important issue when evaluating a coaxial connector for space power applications is the presence of cavities and voids within the components. Some manufacturers advocate a policy that avoids any holes or voids in space level components, particularly in coaxial connector junctions. It is practically impossible to design and produce components without any holes or voids. In this case, the air junctions are usually filled with a sealing compound. The common view is that this will help to create a 100 percent multipaction free design. However, solid dielectrics and sealing compounds have a significantly higher thermal resistivity than dielectrics compensated with axial cavities. The difference is particularly noticeable when using a Fluoroloy H (Rulon H) dielectric, which is commonly found in the coaxial connectors for space power applications. Weirback10 calculates the thermal distribution within coaxial lines using different dielectric materials and geometry. Essentially, this difference indicates that a connector using solid dielectric will handle less average power than a dielectric with cavity compensation.
There are two reasons for such a phenomenon. First, the removed dielectric will reduce the dielectric loss, which is significant for lossy dielectric media such as Fluoroloy H. The increased attenuation dissipates more energy than the increased thermal conductivity of Fluoroloy H can transfer, creating a net increase in dielectric temperature. The second reason is that a drilled out dielectric needs a larger diameter center conductor in order to maintain the same impedance.
Generally speaking, the drilled out dielectric has a higher risk of multipactor, when compared to a solid one, because multipactor is now also possible between the two dielectric surfaces. However, it is possible to reduce the voltage across the holes, which will have two effects. First, this will reduce the risk of multipactor; second, it will improve the average power handing.

Figure 4 Coaxial line with drilled-out dielectric.
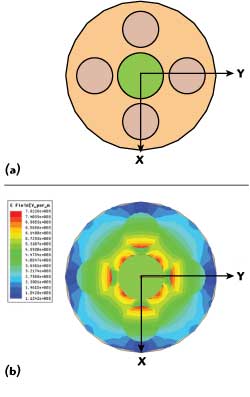
Figure 5 Four-airhole structure (a) and electrical field distribution (b).
Figure 4 shows a possible coaxial line dielectric structure that has good temperature handling and was tested to be multipaction free. The four-hole model and simulated E-field distribution is shown in Figure 5. The simulation was performed using HFSS from Ansoft.14 The response clearly shows that there is a high density electric field inside the holes. However, the shape of the holes creates an asynchronous phase relationship with the signal frequency that is highly unfavorable for electron cloud build-up. An additional multipactor inhibiting feature of this design is the high primary electron energy, defined in eV, required to create the secondary electron emission. While the secondary electron emission coefficient can be high for some dielectrics (including Teflon), the primary electron energy required to initiate this emission is about three times more for Teflon-based dielectrics than for copper. The voltage drop (Vd) across the holes can be calculated using the field calculator in HFSS. The calculation for the dielectric line showed that in a four-hole structure of Fluoroloy H, this voltage is 83 percent of a total voltage (Vmax) between the inner and outer conductors. This is a substantial value. The inhomogeneous voltage distribution is typical for a partial dielectric structure. The higher voltage is always in the portion of the line with the lower dielectric constant. A six-hole structure, as shown in Figure 6, was analyzed to determine the geometrical impact of hole structure to voltage drop. The six-hole structure needs smaller diameter holes to maintain a 50 Ω impedance. This line geometry showed a better voltage ratio of 71 percent. Following this progression, an eight-hole structure as shown in Figure 7 reduced the voltage ratio to 63 percent.

Figure 6 Six-airhole structure (a) and electrical field distribution.

Figure 7 Eight-airhole structure (a) and electrical field distribution (b).
An additional feature that can be modified is the radial position of the holes. Figure 8 shows the holes moved outwards radially within the dielectric structure, where the electromagnetic field is much weaker. In order to maintain a 50 Ω characteristic impedance, the hole diameter needs to be increased as the holes are moved radially away from the center of the line (compare the larger holes of Figure 8 to those of Figure 7). The results show an additional decrease in the voltage ratio, lowering it to 61 percent. A further advantage of the larger hole diameter is the increase in the frequency-distance product, which makes the component less susceptible to multipactor.
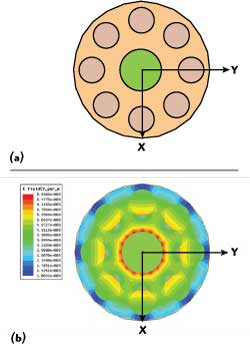
Figure 8 Eight displaced air hole structure (a) and electrical field distribution (b).
Based upon these analyses, the conclusion can be drawn that the eight-hole structure of Figure 8 appears to be the most reliable design in preventing multipactor. This is due to its lower voltage ratio and increased frequency-distance product. It is important to note that both of these performance improvements are due to the placement of the dielectric voids close to the outer conductor to take advantage of the relatively small field density that is present. In reviewing the models presented in this article, the reader must recognize that ideal dielectric voids were used in forming the basis of these conclusions. The ideal holes do not take into consideration burrs, loose material, or other contamination that may be present in actual machined dielectrics that will have a great influence on multipactor. Connectors must be carefully inspected for the absence of foreign objects and loose particles to ensure their ability to meet the requirements of space power applications.
Conclusion
The design of multipaction free coaxial components is a very important part of high power space and vacuum engineering. Here, under the term “coaxial components,” the author is primarily referring to practical applications such as the cable to connector junction and coaxial interfaces with overlapped dielectrics. The differences in the flow of electrons and development of multipactor within a partially loaded dielectric coaxial line versus a traditional air line have been presented. It is apparent that the full analysis of practical coaxial components is extremely complicated. Multipaction detection and test methods are separate issues, which are not covered in this article.
Acknowledgments
The author would like to thank Dr. Perry Malouf from Applied Physics Laboratory, Johns Hopkins University, Dr. Vladimir Volman from Lockheed Martin, Alex Lapidus from L-3 Communications Narda Microwave-West, as well as his colleagues from Astrolab, Stephen Toma and particularly special thanks to Andrew Weirback.
Teflon is a registered trademark of Dupont.
Fluoroloy H and Rulon H are trademarks of Saint Gobain Corp.
References
- J. Rodney M. Vaughan, “Multipactor,” IEEE Transactions on Electron Devices, Vol. 35, No. 7, July 1988, pp. 1172-1180.
- R.A. Kishek, Y.Y. Lau, L.K. Ang, A. Valfells and R.M. Gilgenbach, “Multipactor Discharge on Metals and Dielectric. Historical Review and Recent Theories,” Physics of Plasmas, Vol. 5, No. 5, May 1998, pp. 2120-2126.
- M. Yu, “Power-handling Capability for RF Filters,” IEEE Microwave Magazine, Vol. 8, No. 5, October 2007, pp. 88-97.
- R. Woo, Technical Report 32-1500. Final Report on RF Voltage Breakdown in Coaxial Transmission Lines, NASA, 1970.
- ESA calculator. Calculator can be downloaded free from the ESA website (http://multipactor.esa.int/downloads.html).
- R. Udiljak, “Multipactor in Low Pressure Gas and in Non-uniform RF Field Structures,” Thesis for Degree of Doctor of Philosophy, Chalmers University of Technology, Göteborg, Sweden, 2007.
- R. Udiljak, D. Anderson, M. Lisak, V.E. Semenov and J. Puech, “Multipactor in a Coaxial Transmission Line. I. Analytical Study,” Physics of Plasmas, Vol. 14, No. 3, March 2007.
- V.E. Semenov, N. Zharova, R. Udiljak, D. Anderson, M. Lisak and J. Puech, “Multipactor in a Coaxial Transmission line. II. Particle-in-cell Simulations,” Physics of Plasmas, Vol. 14, No. 3, March 2007.
- N. Rosario, H.F. Lenzing, K.P. Reardon, M.S. Zarro and C.G. Baran, “Investigation of Telstar 4 Spacecraft Ku-band and C-band Antenna Components for Multipaction Breakdown,” IEEE Transactions on Microwave Theory and Techniques, Vol. 42, No. 4, April 1994, pp. 558-564.
- A. Weirback, “Determining the CW Power Rating of Coaxial Components,” High Frequency Electronics, Vol. 7, No. 7, July 2008.
- Rudy Fuks, “Compute Power Rating For Unmatched Lines,” Microwaves & RF, October 1998.
- http://en.wikipedia.org/wiki/Paschen%27s_law.
- MIL-STD-348A, Radio Frequency Connector, Interfaces For.
- HFSS, version 12, Ansoft (part of ANSYS Corp.).
