Estimating & Measuring the Dielectric Constant and Loss Tangent of Dielectric Lattice Structures for Additive Manufacturing (Part 1)

Editor’s Note: As additive manufacturing techniques evolve, these processes offer significant advantages and benefits to the electronics industry. Microwave Journal investigates some of the aspects of this emerging area with a two-part article. This first part introduces the dielectric measurement concepts and some of the challenges. It also includes a portion of a panel discussion where RF dielectric measurement experts from the industry examine some of the most important topics in that area. The second part of this feature will continue the discussion with the panel of experts.

Recent advances in low dielectric constant (Dk) and low loss (Df) resins capable of being used in additive manufacturing (AM) applications have opened the door to creating dielectric lattice structures with tunable dielectric parameters. The ratio of the volume of air to the volume of dielectric lattice can be used to design complex dielectric properties. This technique can be an enabling factor in the realization of metamaterials, complex dielectric lattice structures and artificial dielectrics with performance that, historically, has not been viable with traditionally-fabricated dielectric materials. Increasing the design degrees of freedom brings the challenge of accurately determining the dielectric properties of the material early in the calculation, simulation and measurement process.

This article discusses this challenge and presents a variety of methods used to test dielectric performance, with many only suited to a narrow range of applications. The article also summarizes excerpts from interviews with some of the leading experts in the field. Their insights help frame the applications and benefits of these materials, along with some of the manufacturing challenges.

There have been extensive studies into dielectric materials and methods of characterization, measurement and prediction/simulation, with additional studies of more complex materials over the past 40 to 50 years.^1-10 Methods for measuring simple materials, those with non-magnetic, linear, homogeneous and isotropic dielectric properties, are very well established. The emergence of new methods of dielectric fabrication over the past several years has warranted the exploration of new methods for characterizing, measuring and predicting the behavior of more complex dielectric structures. AM adds a new level of complexity to the design and testing of complex dielectrics since this process can also change the properties of the material. This means that the 2D and 3D structures may exhibit dielectric behavior that cannot readily be predicted or modeled using as-labeled dielectric material properties.

Considerations for Dielectric Structure/Media Testing

This article explores the concepts of measuring and modeling AM dielectric structures. There are a variety of methods for measuring dielectrics. The suitability of a given measurement method is determined by the properties, structure and state of the dielectric material, as well as the testing goals of the dielectric material. With modern, complex AM dielectric structures, there are additional considerations that compound the process of determining the most appropriate test method.

Historically, the type of dielectric material was categorized as either bulk or thin. This described the structure of the dielectric material as either a bulk dielectric that could be measured as a single monolithic structure or a thin dielectric sheet or coating, which requires a different set of testing considerations. In addition to these two categories, a lattice structure or complex dielectric structure must be added. These structures create additional measurement considerations beyond simple bulk dielectric material testing.

Other measurement considerations include the frequency range, the measurement accuracy and the permittivity/permeability range. The intended use of a dielectric generally determines the frequency range. However, in the case of complex dielectric structures, the structure may dictate the operational frequency range and this may deviate from the typical frequency range for the dielectric materials. Measurement accuracy relies on using the best test method, but it may also establish boundaries for the properties and geometry of a given sample. This may be a limiting factor for complex dielectric structures as these structures often have frequency-dependent design features that require certain geometries for optimal performance. Lastly, the permittivity/permeability range of a complex dielectric structure may be difficult to assess initially. Using a dielectric measurement method that is not well-suited to the actual permittivity/permeability range of the dielectric may result in unforeseen errors that are difficult to detect.

Brief on Linearity, Isotropy and Homogeneity of Dielectric Structures/Media

A material that is linear, isotropic and homogeneous will present the same response to a stimulating field regardless of the applied field strength, orientation or how the material’s constitutive parameters are positioned. However, a material may be nonlinear, anisotropic and/or inhomogeneous. These terms mean that the response of a material to a stimulus may depend on the field strength or the orientation of the stimulating field and it may have different profiles based on the constitutive parameter configurations. These factors must be taken into consideration when characterizing, designing or measuring dielectric media or structures. This is because small variations in the material makeup, manufacturing process or assembly can change the material properties, which may then impact the dielectric material features.

To some degree, all materials present some non-idealities that contribute to the overall uncertainty of a given measurement. It can often be difficult to determine the extent of this uncertainty and the appropriateness of various measurement techniques that may be sensitive to these non-idealities. In some cases, it may be appropriate to ignore these non-idealities to some degree and simply use a measurement method that best represents the real-world use of a dielectric structure/media. In other cases, it may be necessary to characterize the dielectric structure or media as completely as possible for the sake of modeling and simulation accuracy.

Common Methods of Dielectric Constant and Loss Tangent Measurement

A wide variety of dielectric measurement methods have been developed to account for the diversity of dielectric materials. The advent of AM and more complex dielectric structures has driven the need to develop measurement processes that best account for capturing the nuances of lattice structures. Due to the relative size and dimensions of lattice structures at various frequencies, there are only a few measurement methods that can be functionally used to make dielectric measurements on dielectric lattices.

Common Dielectric Measurement Methods

• Impedance analyzers/LCR meters
• Parallel plate capacitor or three terminal method (ASTM D150)
• Open-ended coaxial probe
• Dielectric loaded waveguide (filled waveguide)
• Coaxial transmission line (filled transmission line)
• Planar transmission lines
• Focused microwave or mmWave beam (free space)
• Resonant cavity or resonant surface structure
• Split cylinder resonator
• Split post dielectric resonator
• Fabry-Perot open resonator
• Cavity perturbation (ASTM D2520)
• Inductance measurement method.

Most of the common dielectric test methods are not suitable for measuring lattice structures because many of these structures are likely to be based on unit cells. This means that a number of these cells must be arranged to faithfully represent the lattice structure and replicate the desired dielectric performance. In addition, these structures likely will not exhibit the same dielectric behavior if they are improperly arranged into a flat disc or another sample shape that does not recreate the behavior of the dielectric structure. Given that the “bulk” performance of the dielectric lattice is likely what is being tested, this factor alone rules out most dielectric test methods. A unique case of this guideline can occur if the dielectric lattice structure is used as a planar substrate. In this case, the dielectric lattice is likely designed specifically for that purpose and testing using planar transmission line, parallel plate capacitor, split post dielectric resonator, Fabry-Perot open resonator or other methods that can leverage a planar/laminar sample may be appropriate.

For 3D bulk dielectric lattices, loaded waveguide/transmission line, free-space methods like focused mmWave/microwave beam and in some cases, the open-ended coaxial probe method are likely the only applicable test methods. For the open-ended coaxial probe, there may be some limitations in using this method for dielectric lattice structures that do not present a flat, uniform face because air gaps will lead to errors. Issues also arise if there are structural elements significant to the desired dielectric performance that cannot be adequately captured within the fringe fields of the coaxial probe.

For loaded transmission line and waveguide approaches, the physical size of the transmission line/waveguide will impose limitations on the measurement frequency range. Here, the tolerances scale inversely with the frequency to ensure adequate measurement accuracy. Free-space methods have limitations on the sample size and the orientation and isotropicity of the sample must be considered when performing free-space methods like loaded transmission line techniques. Free-space measurements are possible at very high frequencies with relatively small samples, but since the sample size of this method scales with the wavelength, this imposes a constraint on lower frequency measurements.

Expert Discussion on Dielectric Measurements

To gauge the prevailing trends and applications the industry is addressing for dielectric structures, the authors interviewed some of the leading experts in the field. The following are excerpts from interviews conducted with these industry experts on complex dielectric structures and dielectric measurement methods.

What are the applications for these dielectric structures?

Marzena Olszewska-Placha, Ph.D., Vice President for Research & Development, QWED Sp. z o.o.:

Most common materials that are tested with test fixtures, which we develop and offer, are sheet dielectrics, semiconductors and conductive composites. Dielectrics typically include electronic laminates, polymers and ceramic substrates such as LTCC and ULTCC materials. Conductive composite materials cover a wide spectrum of applications from EMC/EMI to energy materials, including anodes for battery cells.

Jonathan Chisum, Ph.D., Associate Professor for Electrical Engineering, University of Notre Dame:

Our research focuses on low-cost and wideband beam scanning lens antennas for applications in 5G/6G mmWave wireless communications, satcom and sensing. Emerging commercial and low-SWaP defense applications demand extremely low-cost and low-power beam scanning antennas. Gradient-index (GRIN) lenses support extremely wideband operation (e.g., 8 to 60 GHz in a single aperture) and provide sufficient degrees of freedom that they can be optimized for wide angle beam scanning with high aperture efficiency.^1,2 However, they are difficult and expensive to fabricate. Due to recent developments in low loss tangent 3D-printed dielectrics, GRIN lens antennas offer a passive beam scanning alternative to the PAA and, when 3D-printed, are low-cost.

Nico Garcia, Ph.D., CEO & Founder, Cheshir Industries:

We are designing and building GRIN lens antennas, a disruptive technology platform with various applications in microwave and mmWave communications and sensing. Our GRIN lens antenna products are low-cost, power-efficient, ultra-wideband alternatives to conventional beamforming antenna solutions.

John Schultz, Ph.D., Chief Scientist, Compass Technologies Group LLC:

At Compass Tech, we are experts in electromagnetic (EM) measurements, especially dielectric measurements and measurement test systems. We also design specialized antennas and probes. For instance, we recently developed a low frequency antenna technology designed to replace bulky low frequency horns, a metamaterial flat lens antenna. Instead of being 30 to 40 in. wide, like the low frequency horns, it is only 2 in. wide. Another example that we are developing is a flexible, slip-on lens for enhancing probe directivity that we manufacture using a fused filament fabricated (FFF) AM technology. We also manufacture a laboratory focus-beam system that we have available at various frequencies with different lens types and technologies.

How and why are precise dielectric constant and loss tangent figures for a dielectric critical for your application? Do these parameters need to be precisely measured or can they be estimated?

Marzena Olszewska-Placha, Ph.D.:

In the case of QWED, I can answer this question from two perspectives, which are related to company activities. Firstly, from the perspective of a vendor of test fixtures for the precise measurements of dielectric properties. And secondly, from the perspective of a company running various research and development activities related to our expertise in designing a wide spectrum of microwave devices. In the design of microwave devices, where interactions between EM fields and materials are involved, e.g., a microwave applicator for bituminous surface treatment, precise knowledge about materials’ parameters, mainly dielectric properties, often as a function of temperature, is required. The more precise this knowledge is, the higher the effectiveness of a design and final real-life device. This experience is our driving force in our second branch of activities, for developing fixtures for microwave characterization of dielectric properties of materials of various kinds.

Jonathan Chisum, Ph.D.:

To realize these benefits, a GRIN lens requires a continuously varying dielectric constant throughout the lens volume. And, to maintain high radiation efficiency, the dielectric should exhibit very low insertion loss. Since there are no methods by which one can realize an ordinary material with arbitrary dielectric constant, GRIN lenses are realized as artificial dielectrics comprising unit cells with varying volume ratios of air and a background or host dielectric to achieve an effective dielectric constant. A curve that illustrates the effects of the volume fill factor on effective permittivity is shown in Figure 1(a).

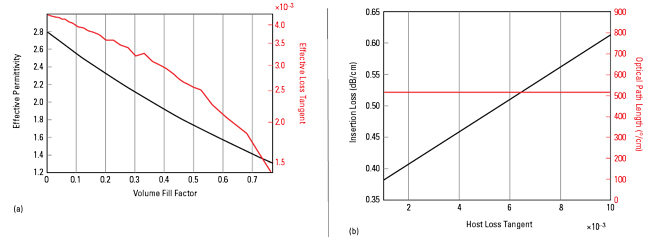
Figure 1 (a) Effective permittivity vs. volume fill factor at 28 GHz. (b) S21/cm vs. host loss tangent at 28 GHz.

Figure 1(b) shows that the optical path length is constant over an order-of-magnitude change in dielectric loss tangent, indicating that phase collimation is insensitive to dielectric loss, but the insertion loss is linear, in dB, with loss tangent. Therefore, it is essential that low loss dielectrics be used and quantified to determine gain from directivity.

Nico Garcia, Ph.D.:

Accurate measurement of the dielectric constants of GRIN materials is crucial. The dielectric constant relates directly to the propagation constant and wave impedance of a GRIN sub-structure; accurate characterization of these parameters is essential to the overall GRIN lens design. Accurate measurement of the loss tangent is less critical assuming that the loss tangent is sufficiently low, ideally around or below 0.002. This is generally easier with alumina and other ceramics, but modern RF composites and laminates are now consistently around this threshold. GRIN lenses generally comprise composite dielectric structures and it is often necessary to take real measurements of these structures’ EM properties before proceeding with design or fabrication. Modern simulation tools are extremely accurate but the simulation model needs to account for manufacturing non-idealities and tolerances; this is only possible if you have real sample measurements on hand with which to compare/tune the simulation model. This step is crucial because GRIN lenses tend to be sensitive to fabrication tolerance. Of course, once you are comfortable with a fabrication paradigm and associated non-idealities, it is sufficient to rely on well-honed simulations. For example, if you are using a relatively simple composite structure like drilled laminates and your manufacturer has excellent tolerances, you may be able to get away without doing any measurements beyond the first round of characterizations. However, if you are working with complicated or unproven structures then high accuracy measurements are essential.

The degree of dielectric precision needed depends on the operating frequency. This is largely because the propagation constant scales with frequency; characterization error of the propagation constant, as a result of characterization error of the dielectric constant, will be exacerbated at higher frequencies. If you design for W-Band or terahertz, you’ll want very precise and accurate EM characterizations only because the propagation constant is so high. Of course, at these frequencies, your mechanical tolerances need to be tighter too because the wavefront will be increasingly sensitive to physical kinks and discontinuities in the structure.

John Schultz, Ph.D.:

For lenses, you don’t want a high permittivity lens, you will get too much reflection. Hence, you need to reduce the permittivity of the lens to enhance overall performance. For practical dielectric applications, such as metamaterial or dielectric lattice structures, you need a pattern with features that are less than a wavelength in order to stay away from resonance. This results in a wide bandwidth structure, which then means you also need to be able to characterize or make measurements of the structure precisely over a wide bandwidth. An approach we have used in the past for dielectric lens development is to make samples with various fill fractions and use the focus-beam system to precisely characterize the complex permittivity of the samples. In this way, we can then take what we know and design a lens with the desired performance.

Conclusion

Additive manufacturing technologies are allowing for even greater degrees of freedom in the design and fabrication of 2D and 3D dielectric structures. Capturing the performance of these structures and being able to predict the dielectric response reliably and accurately is crucial in developing technologies with this new technology. This first part introduced concepts of performing measurements on these new classes of dielectrics. The second part of this article, to be published in an upcoming issue of Microwave Journal dives deeper into these concepts with more from a panel with extensive expertise in dielectric measurement.

References

1. J. Baker-Jarvis, M. D. Janezic and D. C. DeGroot, “High-Frequency Dielectric Measurements,” IEEE Instrumentation & Measurement Magazine, April 2010, Web: https://www.nist.gov/system/files/documents/2017/05/09/Baker-Jarvis-IMMag-April-2010.pdf.
2. J. Obrzut, “Measurement of Materials Dielectric Properties,” Springer Handbook of Material Measurement Method, September, 2006, Web: https://www.nist.gov/publications/measurement-materials-dielectric-properties.
3. J. Krupka, “Frequency Domain Complex Permittivity Measurements at Microwave Frequencies,” Measurement Science and Technology, April 2006, Web: https://iopscience.iop.org/article/10.1088/0957-0233/17/6/R01/meta.
4. J. Krupka, “Microwave Measurements of Electromagnetic Properties of Materials,” Materials, Vol. 14, No. 17, Sept. 2021, Web: www.mdpi.com/1996-1944/14/17/5097.
5. P. I. Dankov, “Two-resonator Method for Measurement of Dielectric Anisotropy in Multilayer Samples,” IEEE Transactions on Microwave Theory and Techniques, Vol. 54, No. 4, June 2006, Web: https://ieeexplore.ieee.org/document/1618573.
6. J. Baker-Jarvis and S. Kim, “The Interaction of Radio-Frequency Fields With Dielectric Materials at Macroscopic to Mesoscopic Scales,” Journal of Research of the National Institute of Standards and Technology, Vol. 117, Feb. 2012, Web: www.ncbi.nlm.nih.gov/pmc/articles/PMC4553869/.
7. Broadband Dielectric Spectroscopy.
8. C.K. Lee, et al., “Evaluation of Microwave Characterization Methods for Additively Manufactured Materials,” Designs, Vol. 3, No. 4, Sept. 2019, Web: www.mdpi.com/2411-9660/3/4/47.
9. E. Costamagna and P. D. Barba, “Inhomogeneous Dielectrics: Conformal Mapping and Finite-element Models” Open Physics, Vol. 15, No. 1, 2017, Web: www.degruyter.com/document/doi/10.1515/phys-2017-0099/html?lang=en.
10. M. A. Sitterly, ”Electromagnetic Characterization of Inhomogeneous Media,” Air Force Institute of Technology, March 2012, Web: https://scholar.afit.edu/cgi/viewcontent.cgi?article=2160&context=etd.