Low Noise Oscillator Based on a Conventional Dielectric Resonator

This article describes an algorithm for the design of a voltage-controlled oscillator (VCO) with an active structure controlled by a sequential feedback circuit containing a high-quality open dielectric resonator. Its effectiveness is illustrated with the design of an X-Band oscillator that meets modern requirements for phase-locked loop (PLL) frequency control systems.

Figure 1 Oscillator topology.

Figure 2 Oscillator assembled in a housing.

Figure 3 DR equivalent circuit.

A microwave oscillator is typically based on a microwave assembly comprising an active two-port amplifier and a resonator, such as a dielectric resonator (DR). Oscillation is normally achieved with parallel feedback (FB). Design techniques for oscillators based on assemblies with parallel FB are well described by Bunin et al.^1,2 Properties of active elements with inherent (i.e., internal) FB are not readily available to oscillator device developers; however, this information is not critical to the design.

In this work, we describe an oscillator development algorithm and verify its efficacy with the design of an X-Band VCO using inherent feedback. The oscillating system is formed by an open DR electromagnetically coupled to a varactor diode (VD) through a microstrip resonator (MSR). The main goal of the dielectric resonator oscillator (DRO) design is to achieve low phase noise, i.e., not to exceed -90 dBc/Hz at 10 kHz offset from the carrier. This level corresponds to or is better than the performance of similar products from leading manufacturers.^3-7 The main application is low phase noise PLL frequency sources,⁸ where there is high interest and demand.⁹

OSCILLATOR DESIGN

The proposed algorithm for DRO design with inherent FB greatly simplifies DRO development. This algorithm consists of two stages: First, one creates a microstrip oscillator on a dielectric substrate using the topology and physical configurations shown in Figures 1 and 2. The required oscillation frequency is achieved by trimming the length of microstrip line (MSL) connected to the input port of the active two-port device, shown as conductor 1 in Figure 1. The oscillation frequency is measured and the length, l, of MSL 1 is recorded. Second, in the housing cup threaded hole, a screw is placed on one end of a dielectric body (e.g., a quartz cylinder) attached to a dielectric disk (i.e., a DR). Moving the case cup along the substrate axis and varying the distance between the DR edge and the substrate surface controls the electromagnetic coupling between conductor 1 and the DR. VCO implementation is enabled by adding an MSR coupled to the DR and connected to a VD.

Selection of the optimal DR position and coupling to the VD is accomplished by a simplified approach, which is demonstrated with the design of an 8 to 10 GHz DRO. The DR equivalent circuit is shown in Figure 3. The characteristics of the coupling structure are defined by the resonant frequency ƒ₀ and the inherent Q-factor, Q₀:

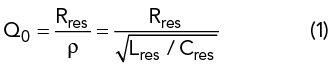
By selecting

The microstrip transmission line model is described by its length, l, longitudinal resistance per unit length, R₀, inductance per unit length, L₀, transverse conductance per unit length, G₀, and capacitance per unit length, C₀. These values can be calculated knowing the MSL wave resistance, Z_w; propagation constant, γ; damping in the line, α; and wavelength, λ_w, in accordance with following:

where λ₀ is the wavelength and ε_eff the effective permittivity of the MSL substrate.

where

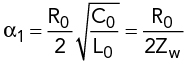
is the damping due to losses in the line metal and

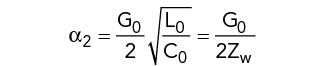
is the damping due to losses in the dielectric.

For example, for an MSL on a polycor substrate with Z_w = 50 Ω, √ε_eff ≈2.5 and known values of α₁ and α₂, one obtains: L₀ = 0.41667 μHn/m, C₀ = 0.16667 nF/m, R₀ = 30 Ω/m, G₀ = 0.01 Sim/m and

Figure 4 Magnitude of the MSR impedance vs. frequency, with C_VD = 0.1 (a) and 0.01 (b) pF.

Figure 4 shows the calculated frequency dependence of the MSR. With a decrease of VD capacitance, by changing the VD voltage, the resonant frequency of the MSR increases, consistent with the theory.

Modeling of coupling between the DR and MSL assumes an ideal transformer (IT), which characterizes the coupling between the DR and the transmission line. The IT properties are defined by

The coupling coefficient β is determined by

Using the coupling model between the DR and MSL, one can calculate the scattering matrix coefficients, which correspond to the theoretical results obtained from the wave equations for the transmission line. The desired resonant frequency of 10 GHz is achieved by varying the VD capacitance between C_VD = 0.01 and 0.1 pF respectively (see Figure 5). Changing the VD capacitance changes the electrical length of the microstrip resonator (i.e., its resonant frequency), which changes the coupling frequencies of the associated oscillator system (i.e., the entire frequency response). The entire frequency response change is quite small, on the order of several MHz.

Figure 5 Magnitude (green) and phase (red) of the MSL impedance with C_VD = 0.01 (a) and 0.1 pF (b).

Figure 6 Dependence of the coupling coefficient, k, on the relative position of the DR to the MSR.

The dependence of the coupling coefficient, k, between the DR and MSR is shown in Figure 6. Lengths l₃ and l₄ are parts of the overall microstrip resonator length (i.e., l = l₃ + l₄), indicating the position of the DR with respect to the microstrip resonator.

where f₁ and f₂ are coupling frequencies that define the frequency tuning of the oscillator.

The frequency response curves of the oscillating system MSL-to-VD interface with various MSR lengths are shown in Figure 7. Figure 8 shows the frequency dependence of the coupling frequency, f1; the Q-factor, Q; and the transfer function versus C_VD.

Figure 7 MSR frequency response vs. C_V and MSR length.

Figure 8 Coupling frequency, f₁, and associated Q-factor, Q₁, vs. C_V, with l₄ = 0.2 cm (1) and 0.3 cm (2).

From the electrical design parameters, Figures 6, 7 and 8 provide dielectric substrate and DR topologies to achieve the optimal, i.e., maximum, effective Q-factors for the oscillating system at a given frequency. The results were verified using ANSYS, the finite-element electromagnetic simulator. The analysis determines the geometric size of the conductor and its position on the polycore substrate, as well.

Figure 9 Power and frequency vs. tuning voltage.

Figure 10 Power and frequency vs. temperature.

MEASUREMENTS

Figure 11 Power and frequency vs. tuning screw position.

Experimental results show that conditions for oscillation are met over a wide range of circuit parameters, i.e., up to 30 percent from the calculated values. This includes DR position with respect to MSL conductor length, resonant frequency, DC bias voltages from 5 to 9 V and VD tuning voltage. DRO characteristics versus VD tuning voltage, temperature variation and mechanical tuning screw position are shown in Figures 9, 10 and 11, respectively.

DRO phase noise heavily depends on the oscillation system Q-factor and, more precisely, on the Q-factor of the resonance curves of the coupling frequency where oscillation occurs. Therefore, considering the low Q-factor of the VD - which does not exceed 500 - the phase noise depends mainly on the required frequency tuning range. The measured phase noise for the 40 MHz tuning range is about ‐80 to ‐85 dBc/Hz at 10 kHz offset from a 10 GHz oscillation frequency. For the 10 MHz frequency tuning range, the phase noise drops to ‐92 dBc/Hz at the same oscillation and offset frequencies (see Figure 12). This tuning range is sufficient for a PLL to compensate for temperature frequency drift, which should not exceed the electrical tuning range.

CONCLUSION

A method for the analysis of complex microwave oscillating systems enables the development of a DRO that meets phase noise and frequency tuning range requirements.n

Acknowledgments

The authors would like to thank Dr. Alexander Chenakin of Anritsu Company for his review and valuable feedback.

References

1. A. V. Bunin, S. V. Vishnyakov, V. M. Gevorkyan and J. A. Kazantsev, “Design of an Oscillator System for Millimeter-Wave Generator,” Proceedings of the 15th International Crimean Conference, September 2005.
2. A. V. Bunin, S. V. Vishniakov and V. M. Gevorkyan, “Design of a Millimeter-Wave Oscillator,” (in Russian), Electronics NTB, No. 6, 2008, pp.106–111.
3. Miteq, internet resource, Web. www.nardamiteq.com/.
4. Eravant, internet resource, Web. www.eravant.com/.
5. Microwave Communications Laboratories Inc., internet resource, Web. www.mcli.com/.
6. Nexyn Corporation, internet resource, Web. www.nexyn.com.
7. Raditek International, internet resource, Web. www.raditek.com.
8. A. Gorevoy, “A Low Noise Oscillator Based on a Conventional Dielectric Resonator,” Microwave Journal, Vol. 56, No. 11, November 2013, pp. 84–94.
9. U. L. Rohde and A. K. Poddar, “DROs Drop Phase Noise,” Microwaves & RF, January 2013.

Figure 12 Phase noise performance.

Vladimir M. Gevorkyan received an engineering degree from the Moscow Power Engineering Institute (National Research University) in 1971 and a PhD in electrophysics in 1979. Since then, he has been teaching at the Moscow Power Engineering Institute and is also engaged in research in the field of electrophysics and microwave technology. Currently he is a professor and the head of the Laboratory of Electrophysics.

Yuri A. Kazantsev received an engineering degree from the Moscow Power Engineering Institute in 1970 and a PhD in electrophysics in 1976. Since then, he has been working and teaching as a professor at the Moscow Power Engineering Institute. His research interests are in electrophysics and microwave technology.