The Marchand balun may be one of the most popular forms of microwave balun used to generate a balanced signal. In particular, the planar coupled-line Marchand balun shows good compatibility with microwave integrated circuits (MIC) and monolithic MICs (MMIC).1 Numerous studies about its design and analysis have been done since it was first introduced in 1944.2 Most designs, however, emphasize maximum power transfer to the balanced load within a specified passband using a quarter-wave transmission line equivalent circuit.
In this article, it will be shown that maximum power transfer does not preserve the balance property of the two balanced outputs. The balance property of the Marchand balun may be more crucial in some applications such as for a mixer. The conditions for preserving the balance property will be explained. Under this limitation, the systematic synthesizing procedure for a coupled-line Marchand balun is then presented to yield the desired passband characteristics.

Design Consideration
The planar coupled-line Marchand balun is shown in Figure 1. Two quarter-wave length coupled lines transform the unbalanced input signal into the balanced output signal across the load.
The coupled line, shown in Figure 2, can be represented by a four-port equivalent circuit through a capacitance matrix transformation.3 Z1 and Z2 are the characteristic impedances of quarter-wave transmission lines, and n is the turn ratio for the transformers. The relations of Z1, Z2 and n to the coupled line with the characteristic impedance, Z, and the coupling constant, k, can be written as4


In the above equations, Zoe and Zoo are the even- and odd-mode impedances of the coupled line. The overall equivalent circuit for the Marchand balun can be readily obtained by replacing the coupled line with the four-port equivalent circuit. Some simplifications and the Richard’s transform for the open- and short-ended quarter-wave transmission lines result in the circuit shown in Figure 3. Here, the subscripts a and b are added to denote the left and right sides of the coupled lines, and N is nb/na. Let the node voltages on each side of the load R be v+(S) and v–(S). Their ratio is

where

According to Equation 5, only when Z1a = Z1b and N = 1(na = nb = n) does the magnitude and the phase of the ratio become 1 and 180°, respectively, regardless of frequency. This means that the Marchand balun should have a symmetrical structure to provide a frequency independent balanced signal.

As an example of this limitation, a theoretical result is shown in Figure 4 for a coupled-line Marchand balun with a balanced load of 100 ? and a 50 ? source impedance for a bandwidth ratio of 1.7:1. The element values in this case are Z1a = 139.74 ?, Z1b = 91.01 ? and na = nb = 1.285. Although the in-band return loss shows a good performance (which means a maximum power transfer to the load without loss), there is a substantial amount of inherent phase error (±5°) within the band of interest, which is crucial in many applications.

Balun Synthesis
Under the previous design limitation, the circuit can be redrawn with the quarter-wave transmission line equivalent circuit shown in Figure 5.
In this circuit, the impedances looking into the source, zi1 and the load, zin are to be calculated as5
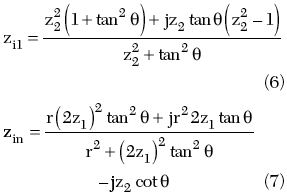
The normalized load resistance r can be expressed as a function of z1 and z2 by


The reflection coefficient of the circuit is then
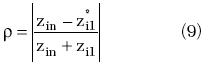
Thus, the synthesis of the Marchand balun is now reduced to the problem of finding the characteristic impedances z1 and z2 to yield the specified passband characteristics, as shown in Figure 6. At ? = ?/2, the reflection coefficient is obtained from Equations 6, 7 and 9.

Substituting r from Equation 8 into Equation 10 yields


Substituting Equation 11 again into Equations 6 and 7, the reflection coefficient in Equation 9 is then dependent only on z2. The reflection coefficient at ? = ?c given by

should satisfy
![]()
to yield the desired passband characteristics.
Using the determined z1 and z2, these values can be translated into the even- and odd-mode impedances using the relations of Equations 1 to 4 as


Synthesis Example
As an example, a coupled-line Marchand balun is synthesized to meet the design requirements for a bandwidth ratio 1.7 (=fU/fL), an in-band return loss of 13 dB for a 100 ? balanced load and a source impedance Z0 = 50 ?. From the given specifications, ?c is calculated to be 66.7° from Equation 12, and ?0 is 0.224. Using Mathsoft’s MathCAD,™ z2 in Equation 13 is determined as 0.59, z1, given by Equation 11, is 0.223. These z1 and z2 impedances correspond to Zoe = 62 ? and Zoo = 19 ? as calculated from Equations 14 and 15, respectively.
A four-coupled stripline is employed to implement Zoe = 62 ? and Zoo = 19 ? on an FR4 (?r = 4.5~4.8) substrate. The cross section geometry is determined using Agilent’s ADS™ and the results are w = 0.35 mm, s = 0.1 mm and h = 1.6 mm.
The frequency responses of the fabricated balun are measured between the unbalanced input and one of the balanced outputs with the other output terminated by 50 ?, with a full two-port calibrated vector network analyzer. The amplitude and phase imbalances are then calculated from the measured data. The results are shown in Figure 7. The measured insertion and return losses show a good agreement with the presented synthesis method and the in-band insertion loss is approximately 3.7 dB. The magnitude ratio between the two balanced outputs is almost 1 and the phase difference from 180° is ±0.5° over the passband, which is due to the imperfections in the fabrication of the two identical coupled-lines. Theoretically, the proposed design has no phase error, as opposed to the conventional design shown previously.
Conclusion
The conventional design based on the maximum power transfer does not provide a good phase balance between the two balanced outputs. The synthesis of a coupled-line Marchand balun preserving the balance is presented to yield the desired passband. The presented synthesis may be useful in applications where the balance between the two outputs is more crucial.
Acknowledgment
This research was supported by the Agency for Defense Development, Korea, through the Radiowave Detection Research Center at the Korea Advanced Institute of Science & Technology.
References
1. S.A. Maas and K.W. Chang, “A Broadband, Planar, Doubly Balanced Monolithic Ka-band Diode Mixer,” IEEE Transactions on Microwave Theory and Techniques, Vol. 41, No. 12, December 1993, pp. 2330–2335.
2. N. Marchand, “Transmission Line Conversion Transformers,” Electronics, Vol. 17, December 1944, pp. 142–145.
3. J.A.G. Malherbe, Microwave Transmission Line Filters, Artech House Inc., Norwood, MA, 1979.
4. C.L. Goldsmith, A. Kikel and H.L. Wilkens, “Synthesis of Marchand Baluns Using Multilayer Microstrip Structure,” International Journal of Microwave and Millimeter-Wave Computer-Aided Engineering, Vol. 2, No. 3, 1992, pp. 179–188.
5. V. Trifunovic and B. Jakanovic, “Review of Printed Marchand and Double-Y Baluns: Characteristics and Applications,” IEEE Transactions on Microwave Theory and Techniques, Vol. 42, No. 8, August 1994, pp. 1454–1462.
Jong-Hwan Lee received his BS and MS degrees in radio science and engineering from Chungnam National University, Daejeon, Korea, in 1998 and 2000, respectively. He is currently working toward his PhD degree. His research interests include RF/microwave circuit and system designs.
Kyung-Whan Yeom received his BS degree in electronics from Seoul National University, Seoul, Korea, in 1980, and his MS and PhD degrees in electrical engineering from the Korea Advanced Institute of Science and Technology (KAIST), Daejeon, Korea, in 1982 and 1988, respectively. From 1985 to 1991, he was with LG Precision, as a principal engineer. From 1991 to 1995, he was with LTI, where he was involved with power amplifier modules for analog cellular phones. He is currently a professor in the department of radio science and engineering at Chungnam National University, Daejeon, Korea. His research interests include the design of hybrid and monolithic microwave circuits and microwave systems.
